黄梅香,博士,讲师,主要研究方向为图像处理、机器学习.E-mail:mxiang_ huang@163.com.
作者简介:

曹树元,硕士研究生,主要研究方向为机器学习、图神经网络.E-mail:shyuan_cao@163.com.

卢福良,博士,教授,主要研究方向为图论及其应用.E-mail:flianglu@163.com.

屠良平,博士,教授,主要研究方向为机器学习、人工智能.E-mail:tuliangping@ustl.edu.cn.
图匹配旨在构造两个图结构之间的节点匹配关系.现有方法普遍忽视节点匹配置信度在图匹配任务中的关键作用.为了充分利用节点间的匹配置信度以控制节点特征信息传递,文中提出基于熵驱动双随机矩阵的图匹配神经网络(Entropy-Driven Doubly Stochastic Matrix-Based Graph Matching Neural Network,EDSGM),通过深度神经网络联合学习节点特征、边特征及图匹配任务的相似度函数,并通过图嵌入方法简化图匹配问题.具体地,EDSGM利用表示图匹配结果的双随机矩阵构造匹配熵,并基于匹配熵构建图内节点嵌入层和跨图信息嵌入层,形成自适应的图嵌入模块.该模型不仅实现特征空间的降维,而且高效传递节点信息,提升匹配精度.此外,EDSGM的所有神经网络模块均可实现端到端的监督训练,同一神经网络能有效处理多个类别的图匹配任务.实验表明,EDSGM在Pascal VOC、SPair-71k、Willow ObjectClass图数据集的多个类别上均取得较高的匹配精度,由此验证匹配熵在优化图节点特征传递效率的同时,可有效提升图匹配精度.
HUANG Meixiang, Ph.D., lecturer. Her research inte-rests include image processing and machine learning.
About Author:
CAO Shuyuan, Master student. Her research interests include machine learning and graph neural network.
LU Fuliang, Ph.D., professor. His research interests include graph theory and its applications.
TU Liangping, Ph.D., professor. His research interests include machine learning and artificial intelligence.
Graph matching is intended to establish node correspondence between two graph structures. Existing methods generally neglect the critical role of node matching confidence in graph matching tasks. To fully utilize the matching confidence between nodes to control the propagation of node feature information, an entropy-driven doubly stochastic matrix based graph matching neural network(EDSGM) is proposed. Node features, edge features and the similarity functions for graph matching tasks are jointly learned by deep neural networks, and the graph matching problem is simplified using graph embedding methods. The matching entropy is constructed using the doubly stochastic matrix representing the graph matching results, and the intra-graph node embedding layer and cross-graph information embedding layer are built to form an adaptive graph embedding module based on the matching entropy. This design not only achieves dimensionality reduction and problem simplification in the feature space, but also makes the propagation of node information more efficient, thereby improving matching accuracy. Furthermore, all neural network modules in EDSGM can be trained end-to-end in a supervised manner, and the same neural network can effectively handle multiple categories of graph matching tasks. Experiments demonstrate that EDSGM achieves state-of-the-art graph matching accuracy across multiple categories on Pascal VOC, SPair-71k, and Willow ObjectClass graph datasets. The results validate that matching entropy enhances the efficiency of node feature propagation and improves graph matching accuracy.
图匹配(Graph Matching, GM)的核心目标是建立两个图结构中关键节点之间的对应关系, 其广泛应用于图像特征匹配、目标跟踪和模式识别等任务[1].例如:在生物信息学领域[2], 图匹配方法为蛋白质结构比对、基因组分析和DNA序列对齐等提供有效解决方案; 在网络分析领域[3], 图匹配不仅能识别社交网络中具有相似兴趣或行为模式的群体, 构建社交网络图谱, 还可用于优化通信网络结构, 提升网络传输性能.
不同于RANSAC(Random Sample Consensus)[4]、ICP(Iterative Closest Point) [5]等点匹配方法, 图匹配方法综合考虑节点的一元相似度[6]、边的二元相似度[7]及高阶超边相似度[8, 9, 10], 建立图结构间的对应关系, 实现图之间匹配相似度的最大化.通过对图结构信息进行编码, 图匹配方法在图的表示和匹配精度方面具有更鲁棒的抗干扰能力和更优的对应关系识别性能.图匹配作为一个经典的排列组合优化问题[11], 具有NP难的计算复杂度, 因此在研究中常采用近似算法求解匹配结果.
传统的图匹配方法主要集中在目标函数的松弛 (如谱松弛[12, 13]、基于双随机松弛[14]等) 和优化策略的设计 (如基于支持向量机学习图模型结构与属性[15]) 两方面, 解决视觉目标匹配等问题.这些经典方法通过不同的松弛策略和优化技术, 为图匹配问题的求解建立系统的理论框架.然而, 传统图匹配方法[12, 13, 14, 15]依赖人工设计图节点特征和组合优化算法, 存在特征表达能力有限、计算复杂度较高、对噪声敏感、泛化能力较弱等不足, 难以应对复杂场景.
相比传统算法, 基于深度学习的图匹配方法具有独特的技术优势和性能特点, 通过端到端学习, 自动提取图结构的高阶语义特征[16], 显著提升噪声鲁棒性[17]、计算效率[18, 19]和跨领域泛化能力[1, 2, 3].
根据利用图高阶信息的方法不同, 现有基于深度学习的图匹配方法主要分为如下两类.1)基于损失函数设计的方法[20, 21].Rolí nek等[20]采用汉明距离作为损失函数, 建立节点和边匹配的联合优化目标, 将图匹配问题转化为最小化节点和边匹配代价的优化问题.Lin等[21]提出COMMON(Contrastive Matching with Momentum Distillation), 设计鲁棒的二次对比学习损失, 利用动量蒸馏策略重新平衡噪声分配, 解决图匹配中双重噪声关联的挑战.然而, 这些方法大多需引入外部度量, 如动量蒸馏模块[21], 会产生额外的计算复杂度.2)基于网络设计的方法[22, 23, 24, 25, 26, 27].Yu等[23]设计CIE(Channel Independent Em-bedding), 将图结构信息编码至节点嵌入, 高效提取图特征, 提升图匹配任务的性能.Fey等[24]引入SplineCNN(Spline-Based Convolutional Neural Networks)[25], 利用B-Spline核将几何特征编码为节点特征, 有效提升模型对图结构特征信息的捕捉能力.Jiang等[26]提出GLMNet(Graph Learning-Matching Network), 采用Laplacian锐化卷积模块, 生成更有辨别力的节点嵌入进行图匹配, 实现面向图匹配任务的最优图结构自适应学习.但是上述方法仅适用于求解KB's QAP(Koopmans-Beckmann's Quadratic Assignment Problem)[28]问题这类特殊情况.为此, Wang等[28]提出NGM(Neural Graph Matching Net-work), 能直接处理更通用的Lawler's QAP[29].NGM利用相似度矩阵构造伴随图, 将图匹配问题转化为伴随图上的节点分类问题, 为复杂图结构匹配问题提供新的思路.
此外, Wang等[17]提出PIA-GM(Permutation Loss and Intra-Graph Affinity Based Graph Matching), 通过图嵌入网络, 将图结构嵌入节点特征向量, 将图匹配问题转换为线性指派问题.在此基础上, 进一步引入跨图嵌入网络, 提出PCA-GM(Permutation Loss and Cross-Graph Affinity Based Graph Matching).尽管上述方法通过强化图内节点和跨图节点特征信息交流, 提升图匹配精度, 但在信息传递机制方面仍存在局限性: 一方面, 这些方法未能充分利用节点匹配对应关系的确定性特征, 导致信息传递过程中存在冗余计算.具体表现为图相似信息的重复传递, 进而引发信息模糊并影响匹配精度.另一方面, 现有方法[17, 27]缺乏动态调整能力, 无法根据节点的匹配关系优化节点特征信息流动路径和强度, 从而在一定程度上限制模型的泛化能力.
为了解决上述问题, 本文提出基于熵驱动双随机矩阵的图匹配神经网络(Entropy-Driven Doubly Stochastic Matrix Based Graph Matching Neural Net-work, EDSGM).设计动态图嵌入网络, 通过浅层网络生成双随机矩阵, 用于计算匹配熵, 动态调控节点间的信息传递强度.并据此构建匹配熵构造模块、匹配熵驱动的节点嵌入层以及跨图信息嵌入层, 将复杂的图匹配问题转化为可解的线性指派问题.还设计匹配熵驱动排列损失函数, 通过Sinkhorn算法将输入矩阵转化为双随机矩阵, 在此基础上施加匹配熵驱动下的更新函数, 生成熵驱动下的预测匹配矩阵, 进而采用交叉熵损失衡量其与真实匹配矩阵的差异.实验表明, EDSGM在Pascal VOC, SPair-71k、Willow ObjectClass图数据集的多个类别上均取得最优的图匹配精度.
给定图对
${{\mathcal{G}}_{1}}=\left( {{\mathcal{V}}_{1}}, {{\mathcal{E}}_{1}} \right)$, ${{\mathcal{G}}_{2}}=\left( {{\mathcal{V}}_{2}}, {{\mathcal{E}}_{2}} \right)$, ,
其中, V1、V2表示节点集合, ε 1、ε 2表示边集合, 节点数
$\left| {{\mathcal{V}}_{1}} \right|={{n}_{1}}$, $\left| {{\mathcal{V}}_{2}} \right|={{n}_{2}}$,
边数
$\left| {{\mathcal{E}}_{1}} \right|={{m}_{1}}$, $\left| {{\mathcal{E}}_{2}} \right|={{m}_{2}}$.
不失一般性, 假定n1≤ n2.为了方便起见, 本文使用下标r∈ {1, 2}表示图的索引.Ar=
本文构建的图结构定义为: 每个图Gr的节点vi对应于自然图像Ir中的关键点kri, 二维像素坐标记为kri=(x, y).
D=
表示双随机矩阵, 满足D
di=(xi1, xi2, …,
表示图G1的第i个节点vi与G2中每个节点匹配的置信度向量, xij表示图G1的第i个节点vi与图G2的第j个节点vj匹配的置信度.
给定图结构G1、G2, 图匹配问题可建模为经典的二次指派问题(Quadratic Assignment Problem, QAP), 其数学形式定义如下:
其中:P∈
${{\mathsf{S}}_{ia, jb}}=\exp \left( \frac{{{\left( {{\mathsf{f}}_{ij}}-{{\mathsf{f}}_{ab}} \right)}^{2}}}{{{\sigma }^{2}}} \right)$,
其中, fij表示边eij对应的特征向量, σ 表示高斯核函数的超参数.当ia=jb时, 节点的相似度也可用上述公式计算.
作为一般的图匹配问题形式, 式(1)称为Lawler's QAP[29], 包含其它的特殊形式, 如KB's QAP[27]:
其中, F1∈
S=F2$\otimes$F1+diag(vec(Sp)),
其中diag(x)表示对角元为x的对角矩阵.
为了有效融合计算机视觉任务中节点间的几何约束关系, Zhou等[30]将相似度矩阵S分解为较小矩阵的克罗内克积:
$\mathsf{S}=\operatorname{diag}\left( \operatorname{vec}\left( {{\mathsf{S}}_{p}} \right) \right)+\left( {{\mathbf{G}}_{2}}\otimes {{\mathbf{G}}_{1}} \right)\operatorname{diag}\left( \operatorname{vec}\left( {{\mathsf{S}}_{q}} \right) \right){{\left( {{\mathbf{H}}_{2}}\otimes {{\mathbf{H}}_{1}} \right)}^{\mathrm{T}}}$.
其中:Gr、Hr(r=1.2)表示图Gr的关联矩阵, 列向量分别记录对应有向边的起始节点和结束节点; Sp∈
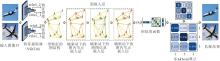
本文提出基于熵驱动双随机矩阵的图匹配神经网络(EDSGM), 具体流程如图1所示.
2.1.1 匹配熵的定义
熵[31]作为信息论中的核心概念, 由Shannon提出, 用于量化系统的不确定性或信息混乱程度, 定义如下:
E=-
其中p(x)表示概率分布.在图匹配任务中, 熵可用于衡量节点匹配的不确定性.当节点匹配关系模糊时, 对应的熵值较高, 反之, 若匹配关系明确, 对应的熵值较低.
近年来, 图神经网络中基于熵的建模方法越来越受到学者们的关注, 如通过信息熵优化图节点特征嵌入权重[32, 33], 基于节点标签熵动态调节的自适应分类模型[34]等.但现有方法大多需要引入外部熵度量, 导致计算量增加, 同时也未能充分考虑节点匹配置信度在图匹配任务中的重要作用.
因此, 为了有效利用节点间匹配置信度, 自适应调控特征信息传递过程, 本文根据节点匹配置信度构造匹配熵.具体地, 给定双随机矩阵:
D=
其中
$\boldsymbol{d}_{i}=\left(x_{i 1}, x_{i 2}, \cdots, x_{i n_{2}}\right) $.
受文献[34]中标签熵的启发, 对于图G1的第i个节点vi, 定义匹配熵:
$E_{1 i}=-\sum_{v_{j} \in V_{2}} \boldsymbol{d}_{i}\left(v_{j}\right) \ln \boldsymbol{d}_{i}\left(v_{j}\right)=-\sum_{j=1}^{n_{2}} x_{i j} \ln x_{i j}, $ (2)
其中di(vj)表示图G1的第i个节点vi与图G2的第j个节点vj匹配的置信度向量.
类似地, 对图G2的第j个节点vj, 定义匹配熵:
$E_{2 j}=-\sum_{i=1}^{n_{1}} x_{i j} \ln x_{i j} $.
在不引起混淆的情况下, 下文统一使用Eri表示图Gr第i个节点vi的匹配熵.
2.1.2 熵驱动下的节点信息传递过程
匹配熵的设计遵循信息论的核心原则:节点匹配熵值反映其匹配结果的不确定性.匹配熵较大的节点, 因匹配置信度较低, 需强化邻接节点的特征输入权重以辅助决策, 同时抑制自身信息输出以避免干扰邻接节点的匹配预测; 匹配熵较小的节点, 因匹配置信度较高, 应强化自身特征传递权重, 同时弱化邻接节点特征信息的输入, 以维护其匹配稳定性.这种动态权重调节机制通过差异化节点特征信息交互策略, 有效平衡图节点特征传递的自主性与协同性, 提升图匹配预测的精度.
具体地, 输入图Gr节点vi的特征向量
$\begin{align} & \mathsf{f}_{ri}^{\left( l \right)}={{f}_{EDSGM}}\left( {{E}_{ri}}, \mathsf{f}_{{{N}_{{{\mathcal{G}}_{r}}}}\left( {{v}_{i}} \right)}^{\left( l-1 \right)}, \mathsf{f}_{ri}^{\left( l-1 \right)} \right) \\ & ={{f}_{norm}}\left( {{E}_{ri}} \right)\mathsf{f}_{{{N}_{{{\mathcal{G}}_{r}}}}\left( {{v}_{i}} \right)}^{\left( l-1 \right)}+g\left( {{E}_{ri}} \right)\mathsf{f}_{ri}^{\left( l-1 \right)}, \end{align}$ (3)
其中, fEDSGM(· )表示在匹配熵驱动下的更新函数, fnorm(Eri)表示对Eri正则化,
g(Eri)=1-fnorm(Eri),
$\boldsymbol{f}_{N_{\mathcal{G}_{r}}\left(v_{i}\right)}^{(l)}=\sum_{v_{j} \in N_{\mathcal{G}_{r}}\left(v_{i}\right)} \alpha_{i j} \boldsymbol{f}_{r j}^{(l)} . $
$\alpha_{i j}=\operatorname{softmax}\left(g\left(E_{r j}\right)\right)=\frac{\exp \left(g\left(E_{r j}\right)\right)}{\sum_{v_{k} \in N_{\mathcal{G}_{r}}\left(v_{i}\right)} \exp \left(g\left(E_{r k}\right)\right)} . $
式(3)中 fnorm(Eri)控制第l层的节点特征信息从第l-1层邻接节点接收的节点特征信息比例, g(Eri)控制储存第l-1层自身节点特征信息的比例.匹配熵Eri较高的节点具有较大的fnorm(Eri)和较小的 g(Eri), 反之亦然.
匹配熵的具体构造及其在节点信息传递过程中的作用示意图如图2所示.
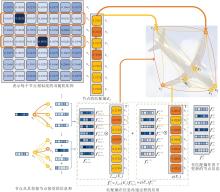 | 图2 匹配熵具体构造及其在节点信息传递过程中的作用示意图Fig.2 Schematic diagram of construction of matching entropy and its role in the process of node information transmission |
EDSGM基于匹配置信度动态调节图节点信息流动: 高置信度节点使用粗橙线向邻接节点传递更多信息, 同时通过细黄线接收少量信息; 低置信度节点则相反, 使用细黄线向邻接节点传递少量信息, 通过粗橙线接收更多信息.图中使用线条粗细直观展示传输信息的强度, 通过这种“ 高输出-低输入” 与“ 低输出-高输入” 的互补机制, 让高置信度节点主导信息扩散, 低置信度节点吸收更多邻接节点信息, 最终实现图节点特征的高效更新.
2.1.3 熵驱动下置信度向量的更新
由匹配熵驱动的图Gr中节点vi的置信度向量di从第l-1到第l层的更新过程如下:
$\begin{array}{l} \boldsymbol{d}_{i}^{(l)}=f_{\mathrm{EDSGM}}\left(E_{r i}, \boldsymbol{d}_{N_{\mathcal{G}_{r}}\left(v_{i}\right)}^{(l-1)}, \boldsymbol{d}_{i}^{(l-1)}\right)=\\ f_{\mathrm{norm}}\left(E_{r i}\right) \boldsymbol{d}_{N_{\mathcal{G}_{r}}\left(v_{i}\right)}^{(l-1)}+g\left(E_{r i}\right) \boldsymbol{d}_{i}^{(l-1)}, \end{array}$
其中,
$\begin{array}{l} \boldsymbol{d}_{N_{\mathcal{G}_{r}}\left(v_{i}\right)}^{(l-1)}=\sum_{v_{j} \in N_{\mathcal{G}_{r}}\left(v_{i}\right)} \alpha_{i j} \boldsymbol{d}_{j}^{(l-1)}, \\ \alpha_{i j}=\operatorname{softmax}\left(g\left(E_{r j}\right)\right)=\frac{\exp \left(g\left(E_{r j}\right)\right)}{\sum_{v_{k} \in N_{G_{r}}\left(v_{i}\right)} \exp \left(g\left(E_{r k}\right)\right)} . \end{array}$
通过上述匹配置信度向量的更新策略, 逐行聚合更新后的向量, 构成第l层熵驱动下的预测匹配矩阵:
$\widehat{\boldsymbol{D}}^{(l)}=\left(\boldsymbol{d}_{1}^{(l)}, \boldsymbol{d}_{2}^{(l)}, \cdots, \boldsymbol{d}_{n_{1}}^{(l)}\right)^{\mathrm{T}} $.
2.2.1 图像特征提取
针对两图匹配问题, EDSGM通过对卷积神经网络(Convolutional Neural Network, CNN)输出的特征图进行双线性插值以提取关键点的特征向量.具体地, 对于自然图像Ir, 关键点kri的特征向量为:
其中: fBi-Interp(kri, T)表示在高维张量T表示的特征空间中, 基于第r幅自然图像Ir的第i个关键点kri的坐标位置进行双线性插值得到的结果; CNN(Ir) 表示自然图像Ir经CNN后输出的特征图.受孪生网络[35]的启发, 两幅输入图像均由同一个CNN处理.
2.2.2 匹配熵驱动下的图内节点嵌入模块
已有研究表明, 相比仅依赖一阶信息的点匹配方法[4, 5], 充分挖掘图结构信息能显著提升匹配鲁棒性[7].为了提升图间节点匹配精度, EDSGM通过匹配熵构建熵驱动下的图内节点嵌入模块, 用于编码二阶图相似度信息.该模块采用图卷积网络[36]的信息传递机制, 在节点特征更新的同时, 考虑其邻域结构信息与自身特征, 并通过匹配熵实现高效的节点特征更新.图Gr第i个节点在第l层沿边传递后的节点特征为:
其中 fEDSGM(· )表示在匹配熵驱动下的更新函数.图Gr第i个节点在第l层自更新后的节点特征为:
通过聚合节点自身特征及其邻接节点的信息, 对节点vi特征的迭代更新过程如下:
fEDSGM(· )、 fnode(· )、 fud(· )可以取任意可微分的、向量到向量的映射.
综上所述, 图结构在熵驱动下的图内信息传递形式表示如下:
其中, fIntra-Conv(· )表示图内节点嵌入函数, Ar∈
2.2.3 匹配熵驱动下的跨图信息嵌入模块
图内节点嵌入模块虽然能有效编码单图结构特征, 但在跨图匹配任务中存在局限, 难以建模图间节点的结构对应关系, 导致匹配特征判别性不足.
为了解决这一问题, 本文在匹配熵驱动的图内节点嵌入模块的基础上, 进一步构造匹配熵驱动的跨图信息嵌入模块.具体地, 使用浅层嵌入网络中预测得到的相似度信息, 通过构建相似度函数及Sinkhorn迭代[37], 生成双随机相似度矩阵D, 编码两个图节点之间的相似度信息.然后, 通过匹配熵构造熵驱动下的预测匹配矩阵
类似于图内节点嵌入模块, 跨图节点的信息传递过程如下.
图G1第i个节点在第1层接收跨图节点信息传递后的节点特征为:
$\boldsymbol{e}_{1 i}^{(l)}=\sum_{v_{j} \in V_{2}} \widehat{D}_{i j} f_{\text {EDSGM-cross }}\left(\boldsymbol{f}_{2 j}^{(l-1)}\right) $,
其中, fEDSGM-cross(· )表示跨图信息传递函数,
其中 fnode-cross(· )表示跨图节点特征自更新函数.由此得到节点vi特征的迭代更新过程如下:
其中 fud-cross(· )表示将两个输入特征张量拼接后输入全连接网络.给定图对G1、G2, 上式刻画的熵驱动下的跨图信息传递形式可表示为
其中 fCross-Conv(· )表示跨图信息嵌入函数.
2.2.4 相似度函数
经过匹配熵驱动下的图内节点嵌入模块和匹配熵驱动下的跨图信息嵌入模块, 两个图结构之间的相似度信息被编码在节点嵌入空间内.因此, EDSGM将式(1)中二阶相似度矩阵S∈
Sij=faffinity(f1i, f2j)=
其中, f1i表示图G1中节点vi的特征向量, f2j表示图G2中节点vj的特征向量, 相似度函数 faffinity(· )表示一个双线性函数, K表示相似度函数中可学习的权重, τ 表示Sinkhorn算法中熵正则项对应的超参数[38].为了保证相似度矩阵S中所有的元素均为非负的, 对其施加指数变换, 即
2.2.5 Sinkhorn网络与线性指派问题的求解
Sinkhorn算法是一种高效求解线性指派问题的迭代方法, 其核心思想是通过交替的行列归一化将任意非负矩阵转化为双随机矩阵.双随机矩阵是离散化排列矩阵的松弛形式.若n1=n2=n, 此时S(l-1)∈
$\begin{array}{l} \boldsymbol{S}^{(l) \prime}=\boldsymbol{S}^{(l-1)} \oslash\left(\boldsymbol{S}^{(l-1)} \mathbf{1}_{n} \mathbf{1}_{n}^{\mathrm{T}}\right), \\ \boldsymbol{S}^{(l)}=\boldsymbol{S}^{(l) \prime} \oslash\left(\mathbf{1}_{n} \mathbf{1}_{n}^{\mathrm{T}} \boldsymbol{S}^{(l) \prime}\right), \end{array}$ (5)
其中, $\oslash$表示矩阵中逐元素的除法, 1n∈ Rn× 1表示一个元素全为1的列向量.由于不同图的大小不同, 输入的相似度矩阵S可能非方阵, 需将其通过虚拟元素(如ε =10-3)填充成一个方阵再进行计算.
通过不断迭代式(5)直至收敛, 最终得到一个双随机矩阵:
D=fSinkhorn(S).
在测试过程中, 作为后处理步骤, 对双随机矩阵D施加匹配熵驱动下的更新函数, 得到熵驱动下的预测匹配矩阵
2.2.6 匹配熵驱动下的排列-交叉熵损失函数
EDSGM采用端到端监督训练框架, 通过Sinkhorn算法将非负矩阵转化为双随机矩阵, 再通过匹配熵构造熵驱动下的预测匹配矩阵, 由此本文提出熵驱动下的排列-交叉熵损失函数(Entropy-Driven Permutation Cross Loss):
$\begin{array}{l} L_{\text {EDSGM-perm }}= \\ \quad-\sum_{i=1}^{n_{1}} \sum_{j=1}^{n_{2}}\left(P_{i j}^{g t} \log \widehat{D}_{i j}+\left(1-P_{i j}^{g t}\right) \log \left(1-\widehat{D}_{i j}\right)\right), \end{array}$,
其中, Pgt∈
2.2.7 算法伪代码
为了充分利用节点间的匹配置信度, 控制节点特征信息传递, 本文提出EDSGM, 伪代码如算法1所示.首先, 利用浅层网络生成初始节点相似度矩阵S, 再应用Sinkhorn算法将S转化为双随机矩阵D.然后, 基于D构造关键指标“ 匹配熵” , 并据此生成熵驱动的预测匹配矩阵
算法1 EDSGM
输入 数据集D具有节点对应关系的图对,
邻接矩阵Ar
输出 预测匹配矩阵
#从数据集中获取图对以及真值标注
$\left\{\left(\boldsymbol{I}_{r}, \left\{\boldsymbol{k}_{r i}\right\}_{i \in V_{r}}, \boldsymbol{A}_{r}\right) \mid r=1, 2\right\}, \boldsymbol{P}^{g t} \in D $;
# 提取CNN特征
if l==1 then
根据式(4), 从
D← fSinkhorn(S);
else
根据式(2)构造匹配熵Eri;
$\begin{array}{l} \boldsymbol{d}_{i}^{(l-1)} \leftarrow f_{\mathrm{EDSGM}}\left(E_{r i}, \boldsymbol{d}_{N_{\Theta_{r}}\left(v_{i}\right)}^{(l-2)}, \boldsymbol{d}_{i}^{(l-2)}\right) ; \\ \widehat{\boldsymbol{D}}^{(l-1)}=\left(\boldsymbol{d}_{1}^{(l-1)}, \boldsymbol{d}_{2}^{(l-1)}, \cdots, \boldsymbol{d}_{n_{1}}^{(l-1)}\right) ; \end{array}$
# 匹配熵驱动下的图内节点嵌入
$\boldsymbol{f}_{r i}^{(l-1)} \leftarrow f_{\text {Intra-Conv }}\left(\boldsymbol{A}_{r}, \boldsymbol{f}_{r i}^{(l-2)}\right) ; $
# 匹配熵驱动下的跨图节点嵌入
$\begin{array}{l} \boldsymbol{f}_{1 i}^{(l)} \leftarrow f_{\text {Cross-Conv }}\left(\widehat{\boldsymbol{D}}, \boldsymbol{f}_{1 i}^{(l-1)}, \boldsymbol{f}_{2 j}^{(l-1)}\right) ; \\ \boldsymbol{f}_{2 j}^{(l)} \leftarrow f_{\text {Cross-Conv }}\left(\widehat{\boldsymbol{D}}^{\mathrm{T}}, \boldsymbol{f}_{2 j}^{(l-1)}, \boldsymbol{f}_{1 i}^{(l-1)}\right) ; \end{array}$
根据式(4), 从
D← fSinkhorn(S);
end if
# 更新熵驱动下的预测匹配矩阵
#端到端训练
$\begin{array}{l} L_{\text {EDSGM-perm }}= \\ \quad-\sum_{i=1}^{n_{1}} \sum_{j=1}^{n_{2}}\left(P_{i j}^{g t} \log \widehat{D}_{i j}+\left(1-P_{i j}^{g t}\right) \log \left(1-\widehat{D}_{i j}\right)\right) . \end{array}$
为了全面评估EDSGM, 在如下3个具有不同规模的基准数据集上进行实验.
1)Pascal VOC数据集[41].共有20类, 包含经过Berkeley关键点注释标定的关键点位置信息, 因为样本在大小、姿态、光照等方面存在很大差别, 这是一个较困难的语义关键点匹配数据集, 也是检验图匹配算法模型有效性的重要数据集.
2)SPair-71k数据集[42].包含70 958个由Pascal VOC 2012数据集和Pascal 3D数据集准备的图像对, 共有18类.每个图像有3~30个关键点标注, 在视点和比例上具有不同的变化.
3)Willow ObjectClass数据集[15].包含来自5个类别的256幅图像, 从Caltech-256(face、duck、wine bottle)数据集和Pascal VOC 2007(car、motorbike)数据集上收集图像, 每类至少包含40幅图像, 所有图像具有一致的方向.
实验时3个数据集上的所有图像在输入网络之前均需经过预处理.为了进行公平对比, 每个物体将根据其边界框(Bounding Box) 进行裁剪, 并统一缩放至256× 256的固定尺寸.
在Pascal VOC数据集上, 通过数据清洗过滤, 最终包含7 020幅训练图像和1 682幅测试图像.
为了验证EDSGM在提升图匹配性能上的有效性, 将正确匹配的关键点对数目除以真值的关键点对总数的结果作为匹配精度.具体地, 对于模型预测得到的排列矩阵
$\boldsymbol{P}=f_{\text {Hungarian }}(\widehat{\boldsymbol{D}}) \in\{0, 1\}^{n_{1} \times n_{2}}$
以及真实匹配情况的排列矩阵Pgt∈
$\text { Accuracy }=\frac{1}{n_{1}} \sum_{i=1}^{n_{1}} \sum_{j=1}^{n_{2}} P_{i j} P_{i j}^{g t} $.
所有实验在64位的Ubuntu 20.04操作系统下运行, 使用NVIDIA RTX 4090 GPU加速训练, 内存为90 GB.实验程序在深度学习框架 PyTorch 2.0.0下, 使用 Python 编译语言实现, 加速库为 CUDA 11.8.为了进行公平对比, EDSGM也采用ImageNet分类任务[43]中的VGG16[44]作为主干网络, 并取VGG16的relu4_2特征和relu5_1特征, 拼接得到两图节点的特征向量fri.
本文选择如下对比方法.
1)HARG-SSVM(Histogram-Attributed Relational Graph Structured Support Vector Machine)[15].基于结构化支持向量机的图匹配学习算法.作为传统图匹配方法, HARG-SSVM与输入物体类型有关, 针对不同输入类别分别学习专用的图模型.
2)GMN(Graph Matching Network)[16].深度图匹配学习领域的先驱工作, 采用VGG16[44]提取图像中的特征, 并用VGG16的浅层特征(relu4_2)与深层特征(relu5_1)构建图匹配相似度矩阵的一阶特征与二阶特征.GMN通过一个不可学习的谱匹配(Spectral Matching, SM) 求解器计算图匹配的相似度.
3)PIA-GM[17].端到端可微分的深度网络, 利用图内节点嵌入网络, 将图匹配问题转化为线性指派问题, 规避具有挑战性的QAP.
4)PCA-GM[17].在PIA-GM的基础上加入跨图节点嵌入网络, 进一步提升匹配精度.
5)GLMNet(Graph Learning-Matching Network)[26].图学习与图匹配的联合优化框架, 自适应学习最优图对, 提升图匹配精度, 采用Laplacian锐化卷积模块增强节点嵌入的判别性, 并设计约束正则化损失函数, 严格满足一对一匹配约束.
6)NGM[28].可直接处理最一般的Lawler's QAP的神经网络模型, 通过相似度矩阵构造伴随图, 将图匹配问题转化为节点分类问题.
在Pascal VOC、Spair-71k、Willow ObjectClass数据集上评估EDSGM的有效性.为了保证公平性, 实验在ThinkMatch开源工具箱上进行, 对于未公开代码的对比方法, 结果引用原文献.
各方法在Pascal VOC数据集上的匹配精度对比如表1所示, 表中黑体数字表示最优值, 斜体数字表示次优值.由表可见, EDSGM在类别aero、bird、boat、bottle、bus、chair、dog、horse、motorbike、person、sheep、sofa上匹配精度最优, 在类别car、cat、cow、plant上匹配精度次优, 平均匹配精度优于GMN、PIA-GM、PCA-GM、NGM, 但略低于GLMNet, 这主要因为GLMNet利用图匹配神经网络, 自适应地学习最适合图匹配任务的最优图对, 并通过Laplacian锐化卷积模块生成区分度更高的节点嵌入, 从而提升匹配精度.EDSGM主要依赖简单的匹配熵自适应调整节点特征传递, 在动物等结构复杂类别的匹配任务中也表现突出.在类别bird、horse、sheep上, 相比GLMNet, EDSGM的匹配精度分别提升4.3%、2.4%、1.1%; 在类别dog上, 相比PCA-GM, EDSGM的匹配精度提升0.9%; 在类别person上, 相比NGM, EDSGM的匹配精度提升0.8%.尽管这些类别的物体结构通常较复杂, 在不同场景下的表现形 式具有多样性, 但EDSGM的图嵌入模块能量化节点的匹配置信度, 并在节点信息传递过程中动态调整节点信息传递的权重.该机制不仅实现节点间信息的高效传播, 还能精准捕捉图结构间的细微差异.这种熵驱动的自适应节点信息传递策略能提升模型对复杂图结构的处理能力, 获得更优的匹配精度.
| 表1 各方法在Pascal VOC数据集上的匹配精度 Table 1 Matching accuracy of different methods on Pascal VOC dataset % |
同时, 在具有刚性结构的类别上, EDSGM的匹配精度也有所提升.在类别sofa、motorbike、aero上, 相比GLMNet, EDSGM的匹配精度分别提升0.7%、0.6%、0.1%; 在类别boat、bus、chair上, 相比NGM, EDSGM的匹配精度分别提升0.8%、1.4%、2.3%.这主要归因于EDSGM能有效抑制低置信度节点的噪声传播, 强化高置信度节点的信息传播, 从而在具有刚性特征的图结构匹配任务中获得更优匹配精度.
各方法在SPair-71k数据集上的匹配精度对比如表2所示, 表中黑体数字表示最优值, 斜体数字表示次优值.
| 表2 各方法在SPair-71k数据集上的匹配精度 Table 2 Matching accuracy of different methods on SPair-71k dataset % |
由表2可见, EDSGM在类别aero、bird、boat、bottle、bus、car、cat、chair、cow、dog、horse、motorbike、plant、sheep、train、tv上匹配精度最优, 在类别person上匹配精度次优, 相比次优的NGM, EDSGM的平均精度提升2.3%.在类别aero、bird、boat、bus、car、cat、cow、horse、mtbike、sheep、tv上, 相比NGM, EDS- GM的匹配精度分别提升1.0%、5.7%, 1.1%、2.3%、0.5%、0.4%、1.8%、0.4%、1.6%、7.0%、1.4%; 在类别dog、plant上, 相比PCA-GM, EDSGM的匹配精度分别提升2.4%、1.7%; 在类别bottle、chair上, 相比GMN, EDSGM的匹配精度分别提升 0.4%、2.6%.
由此说明EDSGM即使面对图结构尺寸和形变变化更大、节点数目更多的图匹配场景, 仍可较好地完成节点匹配任务, 并且性能优于现有的图匹配算法.这归因于在信息传递过程中, EDSGM不仅考虑节点之间的结构关系, 还考虑各节点找到的节点是最优匹配节点的置信度.这种双重考虑使得信息传递更全面, 能更好地捕捉节点之间的语义关系, 提升匹配精度.
各方法在Willow ObjectClass数据集上的匹配精度对比如表3所示, 表中黑体数字表示最优值, 斜体数字表示次优值.
| 表3 各方法在Willow ObjectClass数据集上的匹配精度 Table 3 Matching accuracy of different methods on Willow ObjectClass dataset % |
由表3可见, EDSGM在类别duck、face、wine bottle上达到最优匹配精度, 在类别car、motorbike上达到次优匹配精度, 相比次优的GLMNet, EDSGM的平均精度提升0.3%.在类别bottle上, 相比GLMNet, EDSGM的匹配精度分别提升1.8%; 在类别duck上, 相比NGM, EDSGM的匹配精度提升2.5%; 在类别face上, 相比GMN, EDSGM的匹配精度提升0.5%, 这说明EDSGM在小数据集上也具有有效性.
为了进一步验证EDSGM中图内节点信息嵌入模块(Entropy-Driven Intra-Graph Node Information Embedding, EIE)、跨图节点信息嵌入模块(Entropy-Driven Cross-Graph Node Information Embedding, ECE)和排列-交叉损失函数模块(Entropy Driven Permutation Loss, EPloss)对性能的影响, 在 Pascal VOC 数据集上进行消融实验, 结果如表4所示.
| 表4 在Pascal VOC数据集上各模块对匹配精度的影响 Table 4 Effect of each module on matching accuracy on Pascal VOC dataset % |
由表4可见, EDSGM中各模块对匹配精度均有贡献.增加EIE后, 相比只采用VGG16的EDSGM, 匹配精度提升9.7%, 这一显著提升得益于其在图内节点嵌入过程中不仅考虑节点特征和结构信息, 还考虑每个节点的最优匹配置信度.进一步加入ECE后, 匹配精度提升1.7%, 这得益于ECE比EIE更多考虑跨图的点特征信息.加入EPloss后, 匹配精度又增加0.7%, 这归因于在熵驱动下的排列交叉损失函数能减少不确定性、增强全局一致性以及动态调整优化目标, 从而在复杂的图匹配任务中进一步提高图匹配精度.
各对比方法在Pascal VOC、Spair-71k数据集上的部分匹配结果可视化如图3和图4所示.在图中, 每幅小图下方的a/b表示b个参与匹配的节点中有a个匹配正确, 绿线表示正确匹配结果, 红线表示错误匹配结果.
 | 图3 各方法在Pascal VOC数据集上匹配结果可视化Fig.3 Visualization of matching results for different methods on Pascal VOC dataset |
 | 图4 各方法在SPair-71k数据集上匹配结果可视化Fig.4 Visualization of matching results for different methods on SPair-71k dataset |
由图3可见, 在Pascal VOC数据集上, GMN、PCA-GM和NGM在多个类别的图像关键点匹配上均出现不同程度的错误.在aeroplane类别图像上, 起落架和左右发动机关键点存在误匹配; boat类别的船舱关键点、bus类别的顶部和底部关键点、sofa类别的扶手和靠背关键点也出现错误匹配.这些错误匹配的主要原因在于, 在aeroplane、boat、bus和sofa图像对中, 两幅图像的拍摄角度差异较大, 光照条件显著不同, 导致关键点的特征表达存在较大差异.此外, 在horse类别的图像对中, 由于马的姿态发生显著变化, 加之拍摄视角的不同, 共同导致前后足关键点的错误匹配.EDSGM在这些类别中均能有效规避上述错误, 对于aeroplane、boat、bus、sofa等具有较强刚性结构的物体类别, 尽管拍摄视角和光照条件存在显著差异, 仍能实现精确匹配.同时, 对于horse等结构复杂、姿态多变的动物类别, EDSGM同样匹配结果优异.
由图4可见, 在Spair-71k数据集上, GMN、PCA-GM和NGM在多个类别的图像关键点匹配中均出现不同程度的错误.在bird类别图像中, 两翼和双足关键点存在误匹配; 在boat类别的船舱关键点、bus类别的顶部和底部关键点、cat类别的尾巴和腿部关键点上均出现匹配偏差.此外, horse类别的腿部和双耳关键点也未能准确匹配.这些错误匹配的主要原因在于boat、bus图像对的拍摄视角和光照条件存在显著差异, 导致关键点的特征表达不一致.在bird、cat、horse类别的图像中, 目标的姿态变化较大, 如鸟类的双翼姿态和形状变化、猫的腿部姿态及马的双耳位置变化等, 这些因素均增加关键点匹配的难度, 导致错误匹配的发生.EDSGM在上述类别上的匹配结果均优于对比方法, 其优越性主要归因于提出的熵驱动机制: 一方面, 模型充分考虑匹配图对节点间的结构关系; 另一方面, 引入图节点匹配置信度评估机制.上述双重策略增强节点信息传递的高效性, 有效提升匹配精度.
本文提出熵驱动双随机矩阵的图匹配神经网络(EDSGM), 引入匹配熵机制, 有效克服现有方法忽视图节点匹配置信度的局限.该机制驱动构建自适应图嵌入模块(包含图内嵌入层与跨图嵌入层), 在优化节点特征的同时, 显著提升节点间特征信息传递的效率, 实现精准的节点匹配.在3个数据集上的实验验证EDSGM的优越性与良好的泛化性.端到端可训练的设计也使其能灵活应用于多种图匹配任务.然而, EDSGM在不同任务间的迁移能力仍有待进一步考察.今后将探索该方法在多图匹配及超图匹配等更复杂场景上的应用.
本文责任编委 高 阳
Recommended by Associate Editor GAO Yang
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|