万 青,博士,副教授,主要研究方向为形式概念分析、粗糙集理论、粒计算.E-mail:wqysbe@163.com.
作者简介: 
白 璞,硕士研究生,主要研究方向为形式概念分析、粒计算.E-mail:baipu990622@163.com. 
马盈仓,博士,教授,主要研究方向为粗糙集理论、机器学习、智能计算.E-mail:mayingcang@xpu.edu.cn. 
魏 玲,博士,教授,主要研究方向为形式概念分析、粗糙集理论、概率论.E-mail:wl@nwu.edu.cn.
属性约简是形式概念分析中的热点研究方向之一,研究其动态更新方法在知识发现领域具有重要意义.属性直观图是形式背景的Hasse图表示形式,通过属性直观图可得到保持概念格结构不变的属性约简.因此,文中针对形式背景中属性集变化情况,通过属性直观图的动态更新规律研究此类属性约简的动态更新方法.首先,通过属性的上(下)近邻关系给出属性直观图关系矩阵的定义,并研究该关系矩阵的性质.然后,针对删除属性和增加属性两种情况,分别给出基于关系矩阵的属性直观图的更新方法.最后,借助属性直观图的更新规律给出属性特征的变化规律,进而得到属性约简的动态更新方法.该方法进一步丰富属性约简理论,数值实验说明该方法的有效性.
WAN Qing, Ph.D., associate professor. Her research interests include formal concept analysis, rough set theory and granular computing.
About Author:
BAI Pu, Master student. Her research interests include formal concept analysis and granular computing.
MA Yingcang, Ph.D., professor.His research interests include rough set theory, machine learning and intelligent computing.
WEI Ling, Ph.D., professor. Her research interests include formal concept analysis, rough set theory and probability theory.
Attribute reduction is a prominent research focus in formal concept analysis, and exploring its dynamic update methods is crucial for knowledge discovery. The property pictorial diagram, a Hasse diagram representation of a formal context, can be employed to derive attribute reducts that preserve the concept lattice structure. In this paper, dynamic update methods for attribute reduction are investigated under the changes in the attribute set of a formal context by analyzing the update rules of the property pictorial diagram. First, a relation matrix for the property pictorial diagram is defined using the upper(lower) neighborhood relations among attributes, and its properties are studied. Then, update methods for the property pictorial diagram are proposed based on the relation matrix for two cases: attribute deletion and attribute addition. Finally, based on the update rules of the property pictorial diagram, change rules of attribute characteristics are given, and then dynamic update methods for attribute reduction are developed. The proposed methods further enrich the theoretical foundation of attribute reduction and numerical experiments demonstrate their effectiveness.
自Wille于1982年提出形式概念分析(Formal Concept Analysis, FCA)[1, 2]以来, 该理论已受到学者们的广泛关注.在FCA中, 形式背景和形式概念是其基础定义, 由形式概念的全体在一定偏序关系下形成的Hasse图是该理论的一个核心结构, 被称为概念格.目前, FCA已广泛应用于概念认知学习[3, 4, 5]、机器学习[6, 7]及冲突分析[8, 9]等领域.
属性约简作为FCA的重要研究方向之一, 一直备受学者关注.属性约简的本质是在保持形式背景中某种特性不变的前提下通过删除冗余属性以降低数据维度, 从而使知识的表达更简洁清晰.关于属性约简, 有保持概念格结构不变的属性约简[10]、保持概念格中交(并)不可约元外延不变的属性约简[11, 12]、保持对象粒概念外延不变的属性约简[13].此外, 学者们还将属性约简这一思想应用于不同类型的形式背景和概念格中以简化知识表示[14, 15, 16, 17].另外, 类似于属性约简的思想, 曹丽等[18]和魏玲等[19]从保持形式背景中二元关系不变的角度提出概念约简.Liang等[20]进一步将概念约简应用于概念认知学习.特别值得一提的是, Wan等[21]证明从补背景保持概念格结构不变的属性约简可获得原形式背景的概念约简, 揭示属性约简与概念约简之间的一种内在联系.
随着大数据时代的到来, 数据动态变化已成为常态, 知识的动态更新研究也随之成为学者们关注的焦点.在FCA框架下, 已有学者关注不同类型的概念更新方法[22, 23]、决策规则更新方法[24]和属性约简更新方法[25, 26, 27].属性约简的动态更新研究现阶段主要集中在粒约简方面.曾惠坤等[25]提出在形式背景中添加单个属性或多个属性时粒约简的更新方法.Niu等[26]定义属性重要性, 在决策背景中提出粒约简的更新方法.Li等[27]从图论的角度提出粒约简的更新方法.但是, 目前对于保持概念格结构不变的属性约简的动态更新研究相对较少.
属性直观图是形式背景的一种Hasse图的描述方式, 能直观展示属性与属性之间的关系, 从而得到保持概念格结构不变的属性约简[28].进一步地, 利用属性直观图还可得到三支概念格属性特征的判别方法[29].此外, 还可通过直观图在模糊技能形式背景中建立面向知识结构分析的模糊概念格模型[30].
本文旨在通过属性直观图研究保持概念格结构不变的属性约简更新方法.首先, 通过属性的上(下)近邻关系给出属性直观图关系矩阵的定义, 并研究该关系矩阵的性质.然后, 针对删除属性和增加属性两种情况, 分别给出基于关系矩阵的属性直观图的更新方法.最后, 借助属性直观图的更新规律给出属性特征的变化规律, 进而得到属性约简的动态更新方法.该方法进一步丰富属性约简理论, 数值实验说明该方法的有效性.
定义1[1] 设(G, M, R)为形式背景, 其中:
G={g1, g2, …, gq}
表示对象集, 每个gi(i≤ q)表示一个对象;
M={m1, m2, …, mp}
表示属性集, 每个mj(j≤ p)表示一个属性; R表示G和M之间的二元关系, R⊆G× M.若(g, m)∈ R, 则表示对象g具有属性m.
在形式背景(G, M, R)中, 对于∀ A⊆G, B⊆M, Wille提出一对诱导算子:
A* ={m∈ M|∀ g∈ A, (g, m)∈ R},
B'={g∈ G|∀ |m∈ B, (g, m)∈ R},
其中, A* 表示A中所有对象共同具有的属性集合, B'表示共同具有B中所有属性的对象集合.当二元组(A, B)满足A* =B且B'=A时, 称(A, B)为形式概念, 简称为概念, 并称A为概念的外延, B为概念的内涵.
记L(G, M, R)为形式背景(G, M, R)的所有概念的集合.对
∀ (A1, B1)∈ L(G, M, R), (A2, B2)∈ L(G, M, R),
定义偏序关系:
(A1, B1)⩽(A2, B2)⇔ A1⊆A2(⇔ B1⊇B2).
继而(L(G, M, R), ⩽)构成完备格, 称为概念格, 简记为L(G, M, R).
定义2[10] 设(G, M, R)为形式背景.若∃F⊆M, 使得
L(G, F, RF)≅L(G, M, R),
则称F为(G, M, R)的属性协调集.进一步, 若∀ d∈ F满足
L(G, F-{d}, RF-{d})≇L(G, M, R),
则称F为(G, M, R)的属性约简, 其中
RF=R∩ (G× F).
定义2中的属性约简便是保持概念格结构不变的属性约简.在不引起混淆的情况下, 本文简称为属性约简.
定义3[10] 设形式背景(G, M, R)的所有属性约简为{Fi|Fi为属性约简, i∈ τ }, 其中τ 为一个指标集.属性集M中的属性可分为3类.
1)核心:
$C=\bigcap_{i \in \tau} F_{i}, $
C中的每个属性称为核心属性.
2)相对必要属性集:
$X=\cup_{i \in \tau} F_{i}-\bigcap_{i \in \tau} F_{i}, $
X中的每个属性称为相对必要属性.
3)绝对不必要属性集:
$I=M-\underset{i\in \tau }{\mathop \cup }\, {{F}_{i}}, $
I中的每个属性称为绝对不必要属性.
根据相对必要属性的特点, 若形式背景对应的数表没有两列数值完全相同时, 即没有相同列, 则属性集上的属性仅被分为两类:核心属性和绝对不必要属性.此时, 如果得到绝对不必要属性集, 也就得到核心, 即得到属性约简.因此, 万青[28]通过属性直观图给出属性特征的判别方法, 具体如下.
定义4[28] 设(G, M, R)为形式背景.记
HM={(m', m)|m∈ M},
对∀ ms∈ M, mt∈ M, 若m's⊆m't, 则记
(m's, ms)⩽(m't, mt),
称(HM, ⩽)为(G, M, R)的属性直观图.
记(HM, ⩽)的极大元集合为Max(HM), 极小元集合为Min(HM).需要特别说明的是, 定义4中的属性直观图是指偏序集(HM, ⩽)的Hasse图.此外, 本文后续研究的形式背景均假定其没有相同的列, 即属性集上的属性仅分为核心属性和绝对不必要属性.
定义5[2] 若a、b满足条件a< b且不存在c使得a< c< b成立, 则称a为b的下近邻, 同时称b为a的上近邻, 记作a≺b.
基于定义5, 在形式背景(G, M, R)中, ∀ mi∈ M, mj∈ M, 若
(m'i, mi)≺(m'j, mj),
则称mj为mi的上近邻或称mi为mj的下近邻. 此外, 记属性m的上近邻为
UNm={mj∈ M|(m', m)≺(m'j, mj)},
下近邻为
LNm={mi∈ M|(m'i, mi)≺(m', m)}.
定理1[28] 设(G, M, R)为形式背景, (HM, ⩽)为该形式背景的属性直观图.∀ m∈ M, 则
m∈ I⇔ (m', m)∉Max(HM)
且
$ \bigcap_{m_{s} \in U N_{m}} m_{s}^{\prime}-m^{\prime}=\emptyset .$
实质上, 定理1给出基于属性直观图获取属性约简的方法, 此方法的关键是计算属性的上近邻.
例1 给定形式背景(G, M, R)如表1所示, 其中对象集
G={1, 2, 3, 4, 5, 6},
属性集
M={m1, m2, m3, m4, m5, m6, m7, m8}.
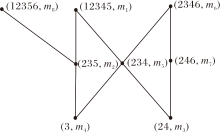
对于表1, 根据定义4, 可得其属性直观图(HM, ⩽)如图1所示.
从图1可得
Max(HM)={(12345, m1), (2346, m6), (12356, m8)}.
因此, 根据定理1可知如果需要求出表1的属性约简, 仅需求出m2, m3, m4, m5和m7的上近邻即可.
| 表1 形式背景(G, M, R) Table 1 Formal context(G, M, R) |
对于属性m2、m3、m4、m5、m7, 其上近邻为
$ U N_{m_{2}}=\left\{m_{1}, m_{8}\right\}, U N_{m_{3}}=\left\{m_{5}, m_{7}\right\}, $
$ U N_{m_{4}}=\left\{m_{2}, m_{5}\right\}, U N_{m_{5}}=\left\{m_{1}, m_{6}\right\}, $
$ U N_{m_{7}}=\left\{m_{6}\right\}, $
因为
$ \cap_{m_{s} \in U N_{m_{2}}} m_{s}^{\prime}-m_{2}^{\prime}=\{1, 2, 3, 5\}-\{2, 3, 5\} \neq \emptyset, $
故由定理1可知m2∉I.类似地, 可验证m4∉I.而
$ \bigcap_{m_{s} \in U N_{m_{3}}} m_{s}^{\prime}-m_{3}^{\prime}=\{2, 4\}-\{2, 4\}=\emptyset, $
故由定理1可知m3∈ I.类似地还可验证m5∈ I.特别地, 因为
$ U N_{m_{7}}=\left\{m_{6}\right\}, \left|U N_{m_{7}}\right|=1, $
故一定有
$ \bigcap_{m_{s} \in U N_{m_{7}}} m_{s}^{\prime}-m_{7}^{\prime} \neq \emptyset $
所以通过定理1可知m7∉I.
综上可得, 表1的绝对不必要属性集为
I={m3, m5}.
于是表1的核心为
C=M-I={m1, m2, m4, m6, m7, m8},
即属性约简为
F={m1, m2, m4, m6, m7, m8}.
为了研究属性直观图的动态更新规律, 下面先依据属性之间的上(下)近邻关系, 给出属性直观图关系矩阵的定义.
定义6 设(HM, ⩽)为形式背景(G, M, R)的属性直观图,
M={m1, m2, …, mp}.
记
R≺={< mi, mj> |(m'i, mi)≺(m'j, mj)},
称R≺为属性的上(下)近邻关系,
上述定义中属性直观图的关系矩阵D, 实质上是在(HM, ⩽)作为偏序集时的关系矩阵中去除自反性与传递性之后得到的, 这些特点可描述如下.
性质1 设(HM, ⩽)为形式背景(G, M, R)的属性直观图,
1)∀ mi∈ M, dii=0.
2)∀ mi∈ M, mj∈ M, 若
3)∀ mi∈ M, ms∈ M, mt∈ M, 若dis=1且dst=1, 则dit=0.
由于从属性直观图可直接得到每个属性的上(下)近邻, 即该Hasse图中有连边的两个节点之间对应属性之间的上(下)近邻关系.由于属性直观图与其关系矩阵是一一对应的, 因此可从关系矩阵D出发得到每个属性的上(下)近邻, 进而得到(HM, ⩽)的极大元与极小元.相关结论如下所示.
性质2 设(HM, ⩽)为形式背景(G, M, R)的属性直观图, D=
1)∀ mj∈ M,
$\sum_{k=1}^{p} d_{k j}=0 \Leftrightarrow\left(m_{j}^{\prime}, m_{j}\right) \in \operatorname{Min}\left(H_{M}\right) ; $
2)∀ mi∈ M,
$\sum_{k=1}^{p} d_{i k}=0 \Leftrightarrow\left(m_{i}^{\prime}, m_{i}\right) \in \operatorname{Max}\left(H_{M}\right) .$
证明 先证1).∀ mj∈ M, 若
$\sum_{k=1}^{p} d_{k j}=0$
则有
d1j=d2j=…=dpj=0,
进而根据定义6可知, ∀ k∈ {1, 2, …, p}, 都有
< mk, mj> ∉R≺,
即mj无下近邻, 因此
(m'j, mj)∈ Min(HM).
反之也是成立的.
再证2).类似于1)的证明过程.
例2 对于例1的属性直观图(HM, ⩽), 由图1可知
(m'2, m2)≺(m'1, m1),
即
< m2, m1> ∈ R≺,
所以根据定义6可得
d28=d35=d37=d42=d45=d51=d56=d76=1.
其余属性之间没有上(下)近邻关系R≺, 于是该关系矩阵中其余元素均为0.综上可得(HM, ⩽)的关系矩阵为:
反之, 在关系矩阵D中, 因其第2行第1列和第2行第8列元素为1, 即
d21= d28=1,
所以可知m2的上近邻为m1和m8, 即
U
又由于D的第1列中
d21=d51=1,
故m1的下近邻为m2和m5, 即
L
类似地, 通过关系矩阵也可得到其它属性的上(下)近邻.
进一步地, 在关系矩阵D中, 因
$ \sum_{k=1}^{8} d_{k 3}=\sum_{k=1}^{8} d_{k 4}=0$
$ \sum_{k=1}^{8} d_{1 k}=\sum_{k=1}^{8} d_{6 k}=\sum_{k=1}^{8} d_{8 k}=0$
故可知(m'3, m3)、(m'4, m4)为极小元, (m'1, m1)、(m'6, m6)、(m'8, m8)为极大元.
下面针对形式背景中属性集的动态变化(删除一个属性和增加一个属性), 基于(HM, ⩽)的关系矩阵D分析属性直观图的变化规律.
为了方便描述, 下文将原形式背景记为(G, Mt, Rt), 其属性直观图记为
记属性m在
下面先给出从原形式背景的属性集Mt中删除属性mk之后Dt和Dt-1之间的关系.
定理2 设
为
$U N_{m_{i}}^{t} \cap L N_{m_{j}}^{t}=\left\{m_{k}\right\}, $
则
证明 ∀ mi∈ Mt-{mk}, 当
mj∈ Mt-{mk}
有
< mi, mk> ∈
继而有
m'i⊂m'k⊂m'j.
又由于
$U N_{m_{i}}^{t} \cap L N_{m_{j}}^{t}=\left\{m_{k}\right\}, $,
因此可知一定不存在
m∈ Mt-{mk},
使得
m'i⊂m'⊂m'j,
所以当删除属性mk后, 有
(m'i, mi)≺(m'j, mj),
于是根据定义6可得
定理2揭示在形式背景中删除一个属性时, 属性集中其余属性上近邻的变化规律.基于定理2, 当删除属性mk时, 记
为由Dt到Dt-1的过渡矩阵, 其中
于是, 在过渡矩阵Dt→ t-1的基础上, 删除Dt→ t-1中的第k行与第k列便可得到删除属性mk后的关系矩阵:
注1 由于在从Dt得到Dt-1的过程中删除第k行和第k列, 此时, 对∀ mi∈ Mt-1, 若i≥ k, 则Dt-1中的第i行(第i列)对应的属性与Dt的第i+1行(第i+1列)对应的属性一致.
下面举例解释当在属性集Mt中删除属性mk时属性直观图的更新方法.
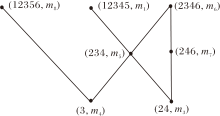
例3 当在例1所示的形式背景中删除属性m2时, 获取(
首先, 根据定理2对Dt中元素进行更新, 得到过渡矩阵
${{D}^{t}}^{\to t-1}={{(d_{ij}^{t\to t-1})}_{p\times p}}.$
因在Dt中只有
以及由
$UN_{{{m}_{4}}}^{t}=\{{{m}_{2}}, {{m}_{5}}\}, $
$LN_{{{m}_{1}}}^{t}=\{{{m}_{2}}, {{m}_{5}}\}, LN_{{{m}_{8}}}^{t}=\{{{m}_{2}}\}$
可得
$UN_{{{m}_{4}}}^{t}\cap LN_{{{m}_{1}}}^{t}=\{{{m}_{2}}, {{m}_{5}}\}, $
$UN_{{{m}_{4}}}^{t}\cap LN_{{{m}_{8}}}^{t}=\{{{m}_{2}}\}.$
故根据定理2可知,
其次, 在Dt→ t-1中删除第2行和第2列, 可得
最后, 根据定义6由Dt-1和
本文约定新增属性mp+1∉Mt且不存在mj∈ Mt有
m'p+1=m'j,
并将新增属性后的形式背景记为(G, Mt+1, Rt+1), 对应的属性直观图记为(
上 (下)近邻关系记为
对于新增属性mp+1, 类似于删除属性的情况, 根据Dt和Dt+1的特点, 先构造由Dt到Dt+1的过渡矩阵Dt→ t+1, 再由过渡矩阵Dt→ t+1得到Dt+1.下面给出Dt与Dt+1的前p行、前p列元素之间的关系.
引理1 设
1)若
2)若
证明 先证1).若
< ml, mp+1> ∉
进而可得
即对∀ j∈ {1, 2, …, p}有
再证2).由定义6知当
< ml, mp+1> ∈
当
< mp+1, ms> ∉
此时分别针对
一方面, 当
< ml, ms> ∉
进而由定义5知m'l⊄m's或存在mv∈ Mt有
m'l⊆m'v⊆m's,
此时, 当增加属性
< ml, ms> ∉
故有
另一方面, 由
< ml, ms> ∈
即m'l⊆m's且不存在mv∈ Mt有
m'l⊆m'v⊆m's.
当增加属性
m'l⊆m'w⊆m's.
若m'l⊄m's, 则与
m'l⊆m'w⊆m's,
则根据
m'l⊆m'p+1⊆m's.
进一步, 由
< ml, ms> ∈
可知, 不存在m∈ Mt有
m'p+1⊆m'⊆m's,
故
引理1揭示在形式背景中增加一个属性时, 原属性集上属性上近邻的变化规律.基于引理1及关系矩阵的性质, 在新增属性mp+1后, 记Dt到Dt+1的过渡矩阵为
其中
由过渡矩阵Dt→ t+1获取Dt+1的方法如定理3所示.
定理3 设
1)若
2)若存在ms∈ Mt有
3)若
证明 先证1).由
< mp+1, ms> ∉
故
2)和 3) 均可用类似于1)的证明过程得证.
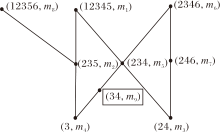
例4 当在例1所示的形式背景中增加属性m9(m'9={3, 4})时, 获取(
首先, 在Dt的基础上按照下述方法添加新的一行和新的一列元素得到Dt→ t+1.因为
m'9⊆m'1, m'9⊆m'5, m'9⊆m'6
且
m'9⊈m'i , i∈ {2, 3, 4, 7, 8},
故
又因m'4⊆m'9且m'i⊈m'9 , i∈ {1, 2, 3, 5, 6, 7, 8}, 故第9列中除了
其次, 利用定理3对过渡矩阵Dt→ t+1中的元素进行更新.因
故可得
又因
故
综上可得
最后, 根据定义6由关系矩阵Dt+1和(
由于利用属性直观图的关系矩阵可得到每个属性的上近邻, 于是结合定理1, 可得基于属性直观图关系矩阵D的属性特征的判断方法如下.
定理4 设(HM, ⩽)为形式背景(G, M, R)的属性直观图, D=
${{m}_{i}}\in I\Leftrightarrow \overset{p}{\mathop{\underset{j=1}{\mathop \sum }\, }}\, {{d}_{ij}}\ge 2$
且
$\underset{{{m}_{s}}\in U{{N}_{{{m}_{i}}}}}{\mathop \cap }\, m{{'}_{s}}-m{{'}_{i}}= \emptyset $,
其中
$U{{N}_{{{m}_{i}}}}=\{{{m}_{j}}\in M|{{d}_{ij}}=1\}$.
证明 $\forall m_{i} \in M$, 若
$\overset{p}{\mathop{\underset{k=1}{\mathop \sum }\, }}\, {{d}_{ik}}\ge 2$,
则有
$\left| U{{N}_{{{m}_{i}}}} \right|\ge 2, $
即
(m'i, mi)∉Max(HM).
又因为
$\bigcap_{m_{s} \in U N_{m_{i}}} m_{s}^{\prime}-m_{i}^{\prime}=\emptyset, $
故根据定理1可知, mi∈ I.
若mi∈ I, 则由定理1可得
(m'i, mi)∉Max(HM),
$\bigcap_{m_{s} \in U N_{m_{i}}} m_{s}^{\prime}-m_{i}^{\prime}=\emptyset .$
而由
(m'i, mi)∉Max(HM)
可知
$\bigcap_{m_{s} \in U N_{m_{i}}} m_{s}^{\prime}-m_{i}^{\prime} \neq \emptyset$
因此
$\sum_{j=1}^{p} d_{i j} \geqslant 2$.
例5 由例2中图1所示属性直观图(HM, ⩽)的关系矩阵可知
$\sum_{j=1}^{8} d_{1 j}=\sum_{j=1}^{8} d_{6 j}=\sum_{j=1}^{8} d_{8 j}=0< 2 $,
$\sum_{j=1}^{8} d_{7 j}=1< 2 $.
因此依据定理4可得
m1∉I, m6∉I, m7∉I, m8∉I.
又因为
$\sum_{j=1}^{8} d_{2 j}=\sum_{j=1}^{8} d_{3 j}=\sum_{j=1}^{8} d_{4 j}=\sum_{j=1}^{8} d_{5 j}=2 $,
于是, 依据定理4需进一步对m2、m3、 m4、m5进行判断, 所得结果为
m2∉I, m4∉I, m3∈ I, m5∈ I.
由上述过程可知, 例1和例5的结果完全一致, 而且从例5的计算过程可发现, 相比定理1, 定理4不需要对只有一个上近邻的属性进行判断, 可简化部分计算.
算法1给出基于定理4获取属性约简的具体过程, 时间复杂度为O(|M|2|G|).
算法1 基于属性直观图关系矩阵的属性约简算法
输入 形式背景(G, M, R)
输出 属性约简 F
initialize D← zeros(p, p), F← Ø , I← Ø
for mi∈ M
for mj∈ M
if < mi, mj> ∈ R≺
dij← 1
else
dij← 0
end if
end for
end for
for ml∈ M
if $ \sum_{j=1}^{p} d_{l j} \geqslant 2 \wedge \bigcap_{m_{s} \in U N_{m_{l}}} m_{s}^{\prime}-m_{l}^{\prime}=\emptyset$
I← I∪ {ml}
end if
end for
F← M-I
return F
下面将在属性直观图动态变化规律的基础上分析属性特征的变化规律.在此, 将原形式背景的核心记为Ct, 绝对不必要属性集记为与It; 删除属性mk之后对应的核心记为Ct-1, 绝对不必要属性集记为It-1; 新增属性
在
本节基于Dt-1的更新规律, 研究属性特征的更新规律, 进而得到属性约简的更新方法.
对于属性mk, 若
$\sum_{i=1}^{p} d_{i k}^{t}=0$,
意味着mk不是其它任何属性的上近邻, 此时删除属性mk, 对其它属性而言定理4中的判定条件不发生改变, 那么其它属性的属性特征就不发生变化.基于此特点, 当删除属性mk时, 可从Dt中第k列的值出发考虑其余属性的属性特征变化规律.
定理5 设
1)当
2)当
证明 先证1).因为
$ \sum_{j=1}^{p-1} d_{i j}^{t-1}=\sum_{j=1}^{p} d_{i j}^{t} $
且
进而由定理4可得mi的属性特征保持不变, 即当mi∈ Ct时, mi∈ Ct-1; 当mi∈ It时, mi∈ It-1.
再证2).若
$\sum_{j=1}^{p} d_{i j}^{t}=1 $
或
$\sum_{j=1}^{p} d_{i j}^{t}> 1 $
且
$\bigcap_{m_{s} \in U N_{m_{i}}^{t}} m_{s}^{\prime}-m_{i}^{\prime} \neq \emptyset $
当
$\sum_{j=1}^{p} d_{i j}^{t}=1 $
时, 则由定理2可知
$\overset{p-1}{\mathop{\underset{j=1}{\mathop \sum }\, }}\, d_{ij}^{t-1}=1$
或
$\overset{p-1}{\mathop{\underset{j=1}{\mathop \sum }\, }}\, d_{ij}^{t-1}=0, $
即
或
因此由定理4可得mi∈ Ct-1.当
$\overset{p}{\mathop{\underset{j=1}{\mathop \sum }\, }}\, d_{ij}^{t}> 1$
且
$\bigcap_{m_{s} \in U N_{m_{i}}^{t}} m_{s}^{\prime}-m_{i}^{\prime} \neq \emptyset$
时, 此时假设
$UN_{{{m}_{i}}}^{t}=\{{{m}_{k}}, {{m}_{r}}\}, $
则有
m'i⊆m'k, m'i⊆m'r
且
m'k∩ m'r-m'i≠ Ø ,
于是可知
m'i⊂m'k∩ m'r.
另外, 当删除属性mk时, 由定理2可知
$UN_{{{m}_{i}}}^{t-1}\subseteq UN_{{{m}_{k}}}^{t}\cup \{{{m}_{r}}\}, $
于是
$\bigcap_{m_{l} \in U N_{m_{k}}^{t} \cup\left\{m_{r}\right\}} m_{l}^{\prime} \subseteq \bigcap_{m_{q} \in U N_{m_{i}}^{t-1}} m_{q}^{\prime}$
又因为
$m_{k}^{\prime} \subseteq \bigcap_{m_{i} \in U N_{m_{k}}^{t}} m_{i}^{\prime}$,
故有
$m_{i}^{\prime} \subset m_{k}^{\prime} \cap m_{r}^{\prime} \subseteq \bigcap_{m_{l} \in U N_{m_{k}}^{t} \cup\left\{m_{r}\right\}} m_{l}^{\prime} \subseteq \bigcap_{m_{q} \in U N_{m_{i}}^{t-1}} m_{q}^{\prime}$.
因此, 依据定理4可得mi∈ Ct-1.
定理5说明在删除属性mk之后, 原形式背景的剩余属性中核心属性仍是新形式背景的核心属性.因此, 基于定理5, 要获取新形式背景的属性约简, 仅需要对原形式背景绝对不必要属性集上的部分属性, 利用定理4在更新后的关系矩阵中对其进行判断即可.
例6 在表1的形式背景中, 已知核心
Ct={m1, m2, m4, m6, m7, m8},
绝对不必要属性集
It={m3, m5}.
在表1中, 当删除属性m2时, 由例2中的Dt可知
于是根据定理5中1)可得,
m1∈ Ct-1, m6∈ Ct-1, m7∈ Ct-1, m8∈ Ct-1,
m3∈ It-1, m5∈ It-1.
由于
m4∈ Ct-1.
综上所述, 当在表1所示形式背景中删除属性m2后, 新形式背景的核心
Ct-1={m1, m4, m6, m7, m8},
绝对不必要属性集
It-1={m3, m5},
属性约简
Ft-1={m1, m4, m6, m7, m8}.
可验证该结论与定理4所得结果一致.
基于定理2、定理4和定理5, 在形式背景中删除属性mk时, 获取属性约简的过程记为算法2, 时间复杂度为
O(|It-{mk}-I0||Mt-{mk}||G|).
算法2 删除mk时属性约简的更新算法
输入 (
输出 属性约简 Ft-1
initialize Ft-1← Ø , I0← Ø , Dt→ t-1← zeros(p, p),
Dt-1← zeros(p-1, p-1), I1← Ø
for mi∈ It-{mk}
if
I0← I0∪ {mi}
end if
end for
if I0=It-{mk}
return Ft-1← Mt-It-{mk}
end if
for mi∈ It-{mk}-I0
if
for mj∈ Mt-{mk}
if
else
end if
end for
end if
end for
Dt→ t-1←
Dt-1← 删除Dt→ t-1的第k行与第k列
for mi∈ It-{mk}-I0
if $\sum_{j=1}^{p-1} d_{i j}^{t-1} \geqslant 2 \wedge \bigcap_{m_{s} \in U N_{m_{i}}^{t-1}} m_{s}^{\prime}-m_{i}^{\prime}=\emptyset$
I1← I1∪ {mi}
end if
end for
Ft-1← Mt-{mk}-I0-I1
return Ft-1
由于在基于属性直观图的属性特征的判别方法中, 关键在于求出属性的上近邻, 因此针对增加一个属性的情况, 下面仍借助
定理6 设(
为(
1)当
2)当
证明 类似于定理5可证.
定理6说明在增加属性${{m}_{p+1}}$时, 原形式背景的绝对不必要属性仍是新形式背景的绝对不必要属性.因此, 想要获取新形式背景的属性约简, 仅需对原形式背景核心中的部分属性及新增属性, 利用定理4在更新后的关系矩阵中对其进行判断即可.
例7 继续以例1的形式背景为例进行解释.
当在表1中增加属性m9(m'9={3, 4})时, 由例4中的Dt+1知
$\begin{aligned} d_{1(p+1)}^{t+1}= & d_{2(p+1)}^{t+1}=d_{3(p+1)}^{t+1}=d_{5(p+1)}^{t+1}=d_{6(p+1)}^{t+1}= \\ & d_{7(p+1)}^{t+1}=d_{8(p+1)}^{t+1}=0 \end{aligned}$
于是由
Ct={m1, m2, m4, m6, m7, m8},
It={m3, m5}
以及定理6中1)可得,
m1∈ Ct+1, m2∈ Ct+1, m6∈ Ct+1, m7∈ Ct+1, m8∈ Ct+1,
m3∈ It+1, m5∈ It+1.
对于属性m4, 由例4的Dt+1可知
故
进而有
$\bigcap_{m_{s} \in U N_{m_{4}}^{t+1}} m_{s}^{\prime}-m_{4}^{\prime}=\{3\}-\{3\}=\emptyset, $
于是根据定理4可得m4∈ It+1.
又因为
$\sum_{j=1}^{9} d_{9 j}^{t+1}=1< 2$,
故根据定理4可得新增属性m9∉It+1.
综上所述, 在增加m9(m'9={3, 4})之后, 新形式背景的核心
Ct+1={m1, m2, m6, m7, m8, m9},
绝对不必要属性集
It+1={m3, m4, m5},
属性约简
Ft+1={m1, m2, m6, m7, m8, m9}.
该结论可由定理4验证其正确性.
基于定理3、定理4和定理6, 在形式背景中增加属性${{m}_{p+1}}$时, 获取属性约简的过程记为算法3, 时间复杂度为
O(|Ct∪ {mp+1}-C0||Mt∪ {mp+1}||G|).
算法3 增加${{m}_{p+1}}$时属性约简的更新算法
输入 (
输出 属性约简 Ft+1
initialize Ft+1← Ø , Dt→ t+1← zeros(p+1, p+1),
Dt+1← zeros(p+1, p+1), C0← Ø , C1← Ø
for mi∈ Mt∪ {mp+1}
for mj∈ Mt∪ {mp+1}
if i≤ p∧ j≤ p
else if m'i⊆m'j
else
end if
end for
end for
Dt→ t+1←
for ml∈ Mt
for ms∈ Mt
if
end if
if
end if
if
end if
end for
end for
Dt+1← Dt→ t+1
for mi∈ Ct
if
C0← C0∪ {mi}
end if
end for
for mi∈ Ct∪ {mp+1}-C0
if $\overset{p+1}{\mathop{\underset{j=1}{\mathop \sum }\, }}\, d_{ij}^{t+1}< 2$
C1← C1∪ {mi}
else if $\bigcap_{m_{s} \in U N_{m_{i}}^{t+1}} m_{s}^{\prime}-m_{i}^{\prime} \neq \emptyset$
C1← C1∪ {mi}
end if
end for
Ft+1← C0∪ C1
return Ft+1
本节评估本文的属性约简动态更新方法的有效性.针对算法1和文献[31]方法的对比, 数据采用随机生成的11个属性个数渐增(|M|=8, 9, …, 18, |G|=18)与11个对象个数渐增(|G|=8, 9, …, 18, |M|=18)的形式背景, 这些形式背景中的二元关系占比约为50%且无相同列.实验结果是取6次实验运行时间的平均值.
由于算法1在计算属性约简时不需要获取概念以及构建概念格, 因此时间复杂度为O(|M|2|G|)远低于文献[31]方法的时间复杂度
算法1和文献[31]方法在属性渐增与对象渐增时的运行时间对比如表2和表3所示.
| 表2 属性渐增时各方法运行时间对比 Table 2 Comparison of running time among different methods during attribute increment s |
| 表3 对象渐增时各方法运行时间对比 Table 3 Comparison of running time among different methods during object increment s |
由表2和表3可见, 属性渐增时, 相比文献[31]方法, 算法1的耗时更少且增幅更平缓.对象渐增时, 算法1仍比文献[31]方法的耗时更少.由此可得, 在仅需要获取属性约简时, 算法1更适用于较大规模的数据.
针对算法1~算法3的对比, 选择4个UCI数据集和4个二元关系占比约为50%的随机生成的形式背景(无相同列), 具体信息如表4所示.此次实验结果仍是取6次实验运行时间的平均值.
| 表4 实验数据集信息 Table 4 Statistics of experimental datasets |
由于UCI数据集上属性值大多数为多值的, 因此, 需对数据进行如下规范化的预处理.
1)对数据集上存在缺失值的情况, 删除缺失值
对应的行(Lung cancer、Spambase数据集).
2)针对数据集上的二值型变量, 保持原始数据不作调整(Zoo、Spambase数据集).
3)对于数据集上分类型的属性, 将其每个取值作为新的属性(Soybean、Lung cancer数据集).
4)对于数据集上存在连续值型的属性, 将属性值平均划分为3个区间, 将每个区间作为独立属性 (Spambase数据集).
此外, 在4个UCI数据集最终生成的形式背景中, 检查并删除所有完全重复的列, 确保属性集上的属性仅被分为核心属性和绝对不必要属性.
表5一方面记录各数据集上的核心属性个数和绝对不必要属性个数, 另一方面, 针对删除属性和增加属性两种情况, 分别记录删除属性和增加属性的属性特征、更新后对应的新形式背景的核心属性个数、绝对不必要属性个数及相应的算法耗时.
| 表5 属性特征的更新结果及相应算法耗时对比 Table 5 Update results of attribute characteristics and running time comparison of corresponding algorithms |
由表5可知:当删除一个属性时,
|It-1|≤ |It|,
即原形式背景中的绝对不必要属性可能变为新形式背景中的核心属性; 当增加一个属性时,
|It+1|≥ |It|,
即原形式背景中的核心属性可能变为新形式背景中的绝对不必要属性.这进一步验证定理5与定理6的正确性.
相比静态方法(算法1), 当删除属性mk时, 算法2仅需对原形式背景的绝对不必要属性集上的部分属性利用定理4判断其属性特征即可, 在最坏情况I0=Ø 时, 算法2的时间复杂度为
O(|It-{mk}||Mt-{mk}||G|),
It-{mk}⊆ Mt-{mk},
也低于算法1的时间复杂度
O(|Mt-{mk}|2|G|).
类似地, 当增加属性
O(|Ct∪ {mp+1}||Mt∪ {mp+1}||G|),
Ct∪ {mp+1}⊆Mt∪ {mp+1},
也低于算法1的时间复杂度
O(|Mt∪ {mp+1}|2|G|).
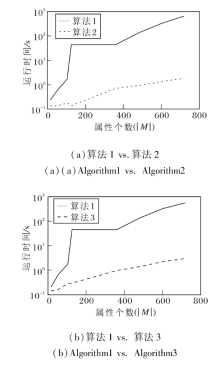
动态更新方法(算法2和算法3)与静态方法(算法1)的耗时对比如图4所示.由图可看出, 随着属性个数的增加, 算法2和算法3的运行时间始终低于算法1, 并且相比算法1, 算法2和算法3的耗时增幅更平缓.由此表明, 在属性集发生改变时, 本文的属性约简的动态更新方法可提升计算效率.
本文借助属性直观图揭示当形式背景的属性集动态变化时属性特征的动态更新规律, 即删除属性时原形式背景的剩余属性中核心属性是新形式背景的核心属性, 增加属性时原形式背景的绝对不必要属性是新形式背景的绝对不必要属性, 继而得到属性约简的动态更新方法.具体地, 通过属性直观图的关系矩阵给出删除一个属性与增加一个属性时属性直观图的更新方法, 基于此利用属性直观图的关系矩阵得到属性特征的更新规律, 从而给出属性约简的更新算法, 并通过数值实验说明属性约简的动态更新方法的有效性, 可提高计算效率.
后续将针对删除对象和增加对象的情况, 基于属性直观图的关系矩阵研究属性约简的更新方法.此外, 基于属性约简与概念约简之间的联系, 可借助基于概念认知学习的图网络数据的节点分类方法, 将本文的属性约简的动态更新方法应用于动态图网络数据节点分类的更新问题上.
本文责任编委 苗夺谦
Recommended by Associate Editor MIAO Duoqian
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|