开放意图分类任务与开放集识别密切相关, 但又具有其特定挑战:一方面, 意图数据多为短文本, 信息密度较低、表述多样, 给表征学习带来困难; 另一方面, 意图之间边界模糊, 部分未知意图可能与多个已知类别具有语义相似性, 导致模型容易误判.近年来, 已有多种方法应用于开放意图分类任务.大致可分为如下三类.

1)基于置信度阈值的方法.此类方法通常借助神经网络分类器输出的概率分布, 设定一个固定或动态的置信阈值, 当预测概率不满足该阈值时, 将样本判为未知类别, 如DOC(Deep Open Classification)^[5]、Maximum Softmax Probability^[8]和OpenMax^[18]等.方法尽管实现简单, 但是对于区分已知意图和未知意图的阈值, 经常难以定义.

2)基于距离度量学习的方法.此类方法强调样本间的特征空间关系, 尝试通过构建类别中心或学习样本间的距离度量函数, 使已知类别之间的边界更清晰, 从而更好地区分未知样本.Chen等^[9]提出ARPL(Adversarial Reciprocal Points Learning), 引入互反点表征开放空间, 结合对抗学习优化样本与互反点的距离, 实现未知类检测.Xu等^[10]提出MDF(Mahalanobis Distance Features), 利用马氏距离度量测试样本与已知类高斯分布的距离.这类方法在提升未知类检测能力方面表现较优, 但仍面临类别内部结构建模不足的问题.

3)多粒度与决策边界建模方法.近年来, 研究者开始关注如何通过显式建模类别边界以提升开放识别能力, 典型代表方法包括ADB(Adaptive Deci-sion Boundary)^[11]、DA-ADB^[12]与MOGB(Multi-gra-nularity Open Intent Classification Method via Adaptive Granular-Ball Decision Boundary)^[14]等.其中, 粒球建模是一种有效的结构建模方式, 通过将类别表示为多个局部球形区域, 使决策边界不再依赖全局中心, 而是更贴合类别内部结构变化.

具体而言, 设训练集上每个样本x_i的特征表示z_i∈ R^d, 类别标签y_i∈ {1, 2, …, K}.ADB假设每个已知类别k的特征表示服从以c_k为中心、以Δ_k为半径的球形分布, 即

$\mathcal{B}_{k}=\left\{\boldsymbol{z}_{i} \in \mathbf{R}^{d}:\left\|\boldsymbol{z}_{i}-\boldsymbol{c}_{k}\right\|_{2} \leqslant \Delta_{k}\right\}$,

其中, c_k表示类别k的样本中心, Δ_k表示通过Soft-plus函数映射的可学习半径.该定义以几何方式刻画每个类别在特征空间中的球形区域, 从而通过训练学习形成具备类内约束的闭合边界结构.模型通过最小化边界损失函数, 促进同类样本聚集在各自的球形区域内部, 并抑制样本越界, 提升分类器的判别能力.在此基础上, DA-ADB引入距离感知系数γ_i, 动态调节不同样本的训练贡献, 特别是边界模糊样本的判别学习.该系数定义如下:

γ_i=exp(‖ z_i- ck2‖₂-‖ z_i- ck1‖₂),

其中, ck1表示样本z_i最近的类别中心, ck2表示样本z_i次近的类别中心.γ_i衡量样本到不同类别中心的相对距离差异, 反映其分类边界的模糊程度.在损失函数中引入γ_i作为样本权重因子, 使分类器更关注边界不明确的样本, 从而强化模型对决策边界附近区域的建模能力.

粒球计算是一种融合人类认知规律与多粒度计算思想的数据表示与分析方法, 最早由Xia等^[16]提出.该方法源于人类“ 由粗到细” 的认知方式^[19], 通过构建不同半径和中心的球形区域以近似和覆盖数据分布, 从而实现对数据的多尺度建模和分层表达.

粒球计算的核心在于利用自适应构造的“ 粒球” 结构划分和表达样本空间.每个粒球由其球心和半径定义, 分别表示球内数据的集中位置和离散程度.在构造初始结构时, 将所有样本聚合形成一个初始粒球, 在满足一定的纯度与样本数量条件下, 粒球会被进一步划分为更小的子球, 逐层细化.这种策略无需预设类别数量, 具有良好的结构适应性^[20].具体而言, 粒球的中心通常为其内部样本向量的均值, 而半径可通过计算样本到中心的平均距离获得.通过设定最小纯度阈值和最小样本数限制, 算法能自动决定是否继续分裂当前粒球, 从而达到自动建模数据局部结构的目的^[16].

粒球计算无需预设类别数量等超参数, 具备良好的结构适应性与可解释性, 广泛适用于分类、聚类、特征选择等任务, 并在实际应用中展现出较强的鲁棒性和泛化性.

设训练集

D_train={(x_i, y_i) }i=1N,

其中, x_i表示输入语句, y_i∈ Y_known表示对应意图标签, N表示意图样本个数.测试集

D_test={(x_j, y_j) }j=1M.

标签空间Y_test包含已知类Y_known与未知类Y_unknown, 即

Y_test=Y_known∪Y_unknown.

开放意图分类任务的目标是构建一个分类模型, 使其在测试阶段能准确识别属于已知类别Y_known的样本, 并将来自未知类别Y_unknown的样本判定为unknown, 从而实现对已知类别识别与开放类别检测的统一处理.

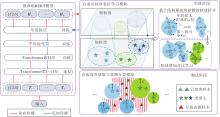
本文提出基于自适应粒球与纯净簇拆分的开放意图分类方法(AGPCS-OIC), 具体架构如图1所示.AGPCS-OIC主要包括两个模块:自适应粒球表征学习模块、决策边界获取与意图分类模块.自适应粒球表征学习模块在训练阶段构建并优化语义空间中的粒球结构, 通过有监督聚类生成初始粒球, 并结合类别纯度与结构特征动态拆分粒球:对纯度不足的“ 混合粒球” 执行类别驱动的拆分, 对半径过大、结构松散的“ 稀疏纯净簇” 执行结构敏感的精细划分.自适应粒球表征学习模块通过粒球聚类与基于最近子类质心的归属计算以调整语义表示, 从而增强类别表示的结构完整性与类别间的区分能力.在此基础上, 决策边界获取与意图分类模块以最终粒球结构为依据, 构建多粒度局部决策边界.在测试阶段, 样本若不落入任何粒球判别区间, 则被视为属于未知类别.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 AGPCS-OIC架构图Fig.1 Architecture of AGPCS-OIC

在表征学习阶段, 本文利用BERT(Bidirec-tional Encoder Representations from Transformers)预训练模型对意图文本进行编码.该模型的前11层Transformer层是被冻结的, 最保留最后一层用作训练, 从最后一层提取

[CLS, T₁, T₂, …, T_L]∈ R^{(L+1)× H}

的词元(Token)嵌入, 其中, CLS表示分类标记, L表示输入文本的词元数量, H表示嵌入维度.对其平均池化以获取句子的语义表示:

x_i=MeanPooling([CLS, T₁, T₂, …, T_L]),

其中MeanPooling(·)表示平均池化.

然后使用一个前馈神经网络层, 将语义表示映射为最终的意图向量:

z_i=ReLU(W_hx_i+b_h),

其中, W_h∈ R^{D× H}表示权重矩阵, b_h∈ R^D表示偏置向量.

接下来, 为了刻画意图类别在特征空间中的多中心结构特征, 针对所有已知类别c∈ Y_known, 在特征空间中进行自适应粒球聚类.该过程以构建初始粒球为起点, 将所有同类样本聚为一个大粒球, 随后依据类别纯度与样本数量划分该粒球:当某粒球的纯度 psc低于预设阈值τ_p, 并且样本数n_s> τ_n时, 从粒球每个类别中各选取一个样本作为伪中心, 将其余样本按最小距离分配给各伪中心, 形成多个新粒球, 直到所有粒球满足约束为止.该策略可确保不同类别样本被有效分离, 避免类间重叠.聚类完成后, 每个已知类别c对应一组粒球集合{g bsc}s=1nc, 其中g bsc表示第c类下的第s个粒球, n_c表示类别c下的粒球总数.每个粒球包含中心 Osc、半径 rsc、主标签 lsc和纯度 psc这4个属性, 具体地, 每个粒球的中心和半径为:

$\boldsymbol{O}_{s}^{c}=\frac{1}{n_{s}} \sum_{z_{i} \in g b_{s}^{c}} \boldsymbol{z}_{i}, r_{s}^{c}=\frac{1}{n_{s}} \sum_{z_{i} \in g b_{s}^{c}}\left\|\boldsymbol{z}_{i}-\boldsymbol{O}_{s}^{c}\right\|_{2}$,

其中, n_s表示粒球g bsc中的样本数量, zi-Osc2表示样本z_i和粒球中心 Osc的欧氏距离.每个粒球的纯度为:

psc= 1nsmaxy∈Yknown|{z_i∈ g bsc|y_i=y}|,

其中, max|· |表示粒球中占比最多类别(主标签 lsc)的样本数.最终保留满足 psc≥ τ_p或n_s≤ τ_n的高质量粒球, 构成已知类别的子类集合, 再使用基于最近子质心归属机制的分类策略, 对于任意样本z_i, 其预测类别由其到所有粒球中心中最近的一个决定:

ŷi=arg minc∈{1, 2, …, K}minsdis(z_i, Osc),

其中, 距离度量dis(· , ·)采用欧氏距离, 用于度量样本与各类中心的相对关系.进一步地, 为了实现可导训练过程, 定义基于粒球距离的类别概率分布:

p(y=c|z_i)= exp(-minsdis(zi, Osc))∑c=1Kexp(-minsdis(zi, Osc)).

在上式中, 分子部分表示样本z_i到类别c粒球中心的距离得分, 分母部分则对所有类别归一化, 形成概率分布.与MOGB^[14]保持一致, 定义分类粒球分类损失函数:

L_gb=- 1N∑i=1Nln p(y_i|z_i),

其中y_i表示样本的真实标签.该损失旨在提升样本对其真实类别中心的亲和度, 从而提升类别判别能力.为了进一步增强类内一致性并拉开类间边界, 本文引入粒球感知对比学习机制.该机制以粒球中心为对比锚点, 对于每个样本z_i, 其正样本定义为所属类别中所有粒球中心, 负样本为所有其它类别的粒球中心.具体地, 给定温度系数τ , 粒球感知对比损失定义如下:

L_contrast=-1N∑i=1Nln(exp(sim(zi, Os* yi)τ)∑c=1K∑s=1ncexp(sim(zi, Osc)τ)),

其中, Os* yi表示标签y_i中与z_i最相似的粒球中心, sim(· , ·)表示余弦相似度.该损失鼓励样本在表示空间中靠近所属类别中心, 同时远离非目标类别中心, 从而优化类别边界结构.

结合上述两种机制, 构建最终的联合训练目标:

L_total=L_gb+λ L_contrast,

其中超参数λ 控制粒球感知对比损失的权重.该联合策略不仅提高表示的判别性, 还增强模型对开放类分布变化的鲁棒性.

粒球的拆分不仅应关注类别纯度, 还应兼顾其在特征空间中的结构合理性.仅依赖纯度判断, 难以处理那些虽由同类样本构成但分布稀疏的粒球.此类粒球可能覆盖过大的空间区域, 从而削弱对未知类的排斥能力.

为此, 本文在纯度拆分的基础上引入结构稀疏性判断机制, 进一步细化纯净但松散的粒球, 提升决策边界的精度与鲁棒性.当粒球纯度 psc≥ τ_p时, 视其为“ 纯净簇” , 并进一步判断其是否满足如下结构稀疏性条件:

maxzi∈gbsc‖ z_i- Osc‖ > δ Ezi∈gbsc‖ z_i- Osc‖ ,

其中, δ 表示结构稀疏系数, Osc表示粒球g bsc的几何中心.该判据用于衡量粒球内部最远样本至粒球中心距离与平均距离之间的比例关系, 若显著偏大, 说明粒球内部存在离散子结构, 即便标签一致, 也可能存在多个潜在簇结构.因此, 以此条件识别结构稀疏粒球, 并触发拆分操作, 防止粒球尺度过大误吸收未知类样本.

在具体拆分过程中, 为了更有效识别粒球边缘结构, 采用基于双中心的再拆分策略.首先选取与几何中心 Osc距离最远的样本z_a作为第一拆分中心:

z_a=arg maxzi∈gbsczi-Osc2.

随后, 以z_a为参照点, 选取粒球内距其最远的样本z_b作为第二拆分中心:

z_b=arg maxzi∈gbsczi-za2.

若z_a≠ z_b, 则以二者作为两个新子簇的初始中心, 依据最小距离原则, 将粒球内其余样本划分至距离更近的中心对应的簇中.随后, 分别对每个子簇重新计算其中心与半径, 从而生成两个新的子粒球.该过程不仅保持类别标签的一致性, 还显著提升粒球的结构紧致性与边界表达能力, 有助于增强模型对未知类的排异能力.为了避免过度划分引发的类别碎片化问题, 拆分操作仅在粒球样本数超过最小阈值(即n_s> τ_n)时才会被执行.

在测试阶段, 模型使用训练阶段得到的子类粒球中心和半径构建每个类别的多粒度决策边界.对每个待测样本z_i, 计算其与所有粒球中心的距离.若对所有粒球中心 Osc, 均有dis(z_i, Osc)> rsc, 则判定为未知类别, 其余的将被分类到对应的已知类别中:

ŷi= unknown, ∀c∈Yknown, dis(zi, Osc)> rscargminc∈Yknown, dis(zi, Osc)≤rscdis(zi, Osc), 其它

基于文献[11]方法, 本文选择在如下5个常用数据集上进行实验.

1)BANKING数据集^[21].涵盖77类意图的银行客服数据, 类别重叠较多, 分类难度较大.

2)OOS数据集^[22].包含150个意图和1 200个未知查询, 适用于开放识别任务.

3)HWU64数据集^[23].跨越21个领域的多意图数据集, 共计64类意图, 场景丰富.

4)SNIPS数据集^[24].由14 484条语句组成, 包含7个不同的意图类别.

5)StackOverflow数据集^[25].包含3 370 528个编程问题标题的数据集, 涵盖20类.

为了全面评估AGPCS-OIC在不同开放性水平下的表现, 设置不同的已知类别比例(25%、50%和75%)以模拟不同程度的开放场景.在表征学习阶段, 采用预训练的BERT作为特征提取器, 仅微调其最后一层参数以增强语义区分能力.训练批次大小设为128, 学习率设为2e-5, 最大训练轮次设为100.粒球拆分和筛选阶段使用的纯度阈值均设为0.9, 最小样本数阈值根据不同的数据集规模进行调整.

此外, 为了增强实验结果的稳定性和可靠性, 所有实验均在3个不同随机种子下独立运行3次, 最终结果取3次实验的平均值.

本文采用整体准确率(Accuracy, ACC)和整体F1分数(F1-A)作为评估方法综合性能的主要指标.此外, 为了更全面分析方法在开放场景下的识别能力, 进一步计算已知类别的F1分数(F1-K)和未知类别的F1分数(F1-U), 分别衡量方法在已知意图识别与未知意图检测方面的性能.

本文选取如下7个具有代表性的开放意图分类方法作为对比方法, 验证AGPCS-OIC的有效性.

1)DOC^[5].通过高斯拟合建立概率阈值, 进行开放意图分类.

2)文献[8]方法.基于softmax最大值作为置信度进行开放意图分类.

3)ADB^[11].基于类内样本自适应构建质心和决策边界.

4)DA-ADB^[12].在ADB基础上学习距离感知的意图表示, 获得适当的决策边界.

5)MOGB^[14].多粒度开放意图分类方法, 能精准建模复杂意图结构, 并提升未知意图的识别能力.

6)OpenMax^[18].训练时学习类别中心, 并利用类间距离进行开放空间建模与重校准.

7)OLT(Open-World Lottery Ticket)^[26].提出开放世界彩票票据假设, 通过剪枝获得可信子网络, 有效提升未知意图检测能力.

在BANKING、OOS、HWU64、SNIPS、Stackoverflow数据集上, 在不同已知类别比例(25%、50%、75%)下, 各方法的指标值对比如表1~表6所示, 表中黑体数字表示最优值.

表1

Table 1

表1(Table 1)

表1 已知类别比例为25%时各方法在5个数据集上的F1分数对比 Table 1 F1 score comparison of different methods at a known class proportion of 25% on 5 datasets % 方法 BANKING OOS HWU64 SNIPS Stackoverflow F1-U F1-K F1-U F1-K F1-U F1-K F1-U F1-K F1-U F1-K 文献[8]方法 41.43 50.55 50.88 47.53 36.47 49.80 0.00 56.48 13.03 42.82 DOC 61.42 57.85 81.98 65.96 0.00 48.14 34.67 65.32 41.25 49.02 OpenMax 51.32 54.28 75.76 61.62 46.82 54.99 61.92 43.56 49.29 52.60 ADB 84.32 70.91 91.18 75.03 78.41 68.41 58.92 69.12 90.88 78.82 DA-ADB 85.85 72.14 93.41 78.10 83.92 69.75 72.80 73.90 91.16 77.82 OLT 86.86 72.18 62.68 81.05 89.98 70.15 80.37 63.33 91.58 73.45 MOGB 88.29 74.50 93.35 61.18 89.64 61.45 71.36 72.63 92.75 75.35 AGPCS-OIC 90.79 75.97 95.47 81.79 90.19 73.47 80.89 78.31 93.24 81.60

表1 已知类别比例为25%时各方法在5个数据集上的F1分数对比 Table 1 F1 score comparison of different methods at a known class proportion of 25% on 5 datasets %

表2

Table 2

表2(Table 2)

表2 已知类别比例为50%时各方法在5个数据集上的F1分数对比 Table 2 F1 score comparison of different methods at a known class proportion of 50% on 5 datasets % 方法 BANKING OOS HWU64 SNIPS Stackoverflow F1-U F1-K F1-U F1-K F1-U F1-K F1-U F1-K F1-U F1-K 文献[8]方法 41.19 71.97 57.62 70.58 35.09 71.04 7.12 77.40 23.99 66.91 DOC 55.14 73.59 79.00 78.25 0.12 67.29 54.89 83.97 25.44 66.58 OpenMax 54.33 74.76 81.89 80.54 55.12 74.04 14.23 78.31 45.00 70.49 ADB 78.96 81.11 86.87 83.02 71.65 77.65 62.17 82.98 87.34 85.68 DA-ADB 79.09 79.68 89.83 83.91 80.66 77.69 66.58 80.05 87.21 85.01 OLT 79.29 75.35 60.02 78.41 79.03 72.88 63.89 75.43 87.09 79.77 MOGB 81.04 81.53 85.04 62.60 78.51 62.83 62.42 83.03 80.84 70.13 AGPCS-OIC 83.27 82.16 91.31 86.22 83.64 80.93 70.16 87.74 90.52 88.75

表2 已知类别比例为50%时各方法在5个数据集上的F1分数对比 Table 2 F1 score comparison of different methods at a known class proportion of 50% on 5 datasets %

表3

Table 3

表3(Table 3)

表3 已知类别比例为75%时各方法在5个数据集上的F1分数对比 Table 3 F1 score comparison of different methods at a known class proportion of 75% on 5 datasets % 方法 BANKING OOS HWU64 SNIPS Stackoverflow F1-U F1-K F1-U F1-K F1-U F1-K F1-U F1-K F1-U F1-K 文献[8]方法 39.23 84.36 59.08 82.59 32.07 82.79 6.52 85.77 33.96 80.88 DOC 50.60 83.91 72.87 83.69 0.00 79.55 51.67 89.40 16.76 78.95 OpenMax 50.85 84.64 76.35 73.13 59.33 80.48 11.03 86.15 44.87 82.11 ADB 63.38 84.72 83.67 87.21 55.64 81.44 73.35 91.66 73.86 86.80 DA-ADB 67.92 84.91 84.67 85.69 64.19 81.74 68.62 87.42 74.06 86.92 OLT 62.70 76.09 60.00 75.97 64.90 75.98 76.97 78.22 72.77 81.92 MOGB 71.27 87.09 71.80 61.29 55.87 60.11 73.62 92.55 57.58 68.86 AGPCS-OIC 70.78 85.54 85.65 88.55 72.18 84.23 77.23 93.05 73.40 87.03

表3 已知类别比例为75%时各方法在5个数据集上的F1分数对比 Table 3 F1 score comparison of different methods at a known class proportion of 75% on 5 datasets %

表4

Table 4

表4(Table 4)

表4 已知类别比例为25%时各方法在5个数据集上的总体性能对比 Table 4 Overall performance comparison of different methods at a known class proportion of 25% on 5 datasets % 方法 BANKING OOS HWU64 SNIPS Stackoverflow F1-A ACC F1-A ACC F1-A ACC F1-A ACC F1-A ACC 文献[8]方法 50.09 43.67 47.62 47.02 49.01 40.18 37.65 28.57 37.85 28.67 DOC 58.03 56.99 66.37 74.97 45.31 24.60 55.10 45.63 47.73 42.74 OpenMax 54.14 49.94 61.99 68.50 54.51 46.44 49.68 59.57 45.98 40.28 ADB 71.58 78.70 75.45 86.38 66.08 71.90 65.72 58.57 80.83 86.72 DA-ADB 72.83 80.36 78.49 89.65 70.58 78.22 73.54 69.57 80.05 87.01 OLT 63.03 80.74 81.16 78.62 66.02 85.04 76.52 75.48 82.96 87.94 MOGB 75.19 83.08 62.00 88.68 63.11 84.11 72.20 68.00 78.25 88.73 AGPCS-OIC 76.71 86.30 82.14 92.65 74.46 85.32 79.17 76.76 83.54 89.85

表4 已知类别比例为25%时各方法在5个数据集上的总体性能对比 Table 4 Overall performance comparison of different methods at a known class proportion of 25% on 5 datasets %

表5

Table 5

表5(Table 5)

表5 已知类别比例为50%时各方法在5个数据集上的总体性能对比 Table 5 Overall performance comparison of different methods at a known class proportion of 50% on 5 datasets % 方法 BANKING OOS HWU64 SNIPS Stackoverflow F1-A ACC F1-A ACC F1-A ACC F1-A ACC F1-A ACC 文献[8]方法 71.18 59.73 70.41 62.96 69.95 56.78 63.34 57.97 63.01 52.42 DOC 73.12 64.81 78.26 77.16 65.25 46.78 78.15 72.50 62.84 52.53 OpenMax 74.24 65.31 80.56 80.11 73.46 64.31 65.50 59.82 68.18 60.35 ADB 81.05 79.20 83.07 84.43 77.47 73.48 78.82 73.57 85.83 86.40 DA-ADB 79.67 78.52 83.99 87.29 77.73 79.00 77.35 73.69 85.21 86.02 OLT 71.96 77.31 78.55 75.98 69.38 77.63 80.58 74.00 84.95 85.97 MOGB 81.52 80.58 62.90 78.82 63.31 73.20 78.91 73.86 71.11 76.71 AGPCS-OIC 82.19 82.31 86.29 89.10 81.01 82.56 84.23 80.52 88.92 89.72

表5 已知类别比例为50%时各方法在5个数据集上的总体性能对比 Table 5 Overall performance comparison of different methods at a known class proportion of 50% on 5 datasets %

表6

Table 6

表6(Table 6)

表6 已知类别比例为75%时各方法在5个数据集上的总体性能对比 Table 6 Overall performance comparison of different methods at a known class proportion of 75% on 5 datasets % 方法 BANKING OOS HWU64 SNIPS Stackoverflow F1-A ACC F1-A ACC F1-A ACC F1-A ACC F1-A ACC 文献[8]方法 83.60 75.89 82.38 74.07 81.76 72.65 72.56 71.49 77.95 72.17 DOC 83.34 76.77 83.59 78.73 77.93 68.12 83.11 79.96 75.06 68.91 OpenMax 84.07 77.45 73.16 76.80 80.05 76.80 73.63 72.20 79.78 74.42 ADB 84.36 79.18 86.37 86.32 80.91 75.62 88.61 86.71 85.99 82.78 DA-ADB 84.71 79.94 85.68 85.41 81.39 77.48 84.29 81.57 86.11 82.89 OLT 75.54 73.68 75.84 74.29 75.18 76.58 89.14 88.00 85.35 82.26 MOGB 86.82 82.69 61.38 67.83 60.02 59.95 89.39 87.71 68.16 64.42 AGPCS-OIC 85.29 81.40 88.52 87.20 83.98 81.57 89.55 87.90 86.17 82.74

表6 已知类别比例为75%时各方法在5个数据集上的总体性能对比 Table 6 Overall performance comparison of different methods at a known class proportion of 75% on 5 datasets %

由表1~表6可见, 在F1-A和ACC指标上, AGPCS-OIC在多个数据集上均表现出显著优势, 尤其是在已知类别占比较低(25%)时.随着已知类别比例的提升, 性能优势依然存在但提升相对减小.这表明, AGPCS-OIC在高开放性场景下具备更强的泛化能力与未知意图检测能力, 同时在封闭程度较高时也能保持稳定的分类性能.

在已知类别比例较低的场景中, 类别间的分布往往更稀疏, 语义边界更模糊.AGPCS-OIC在该场景下表现出更明显的性能提升, 主要得益于AGPCS-OIC在复杂语义分布建模方面的结构优势.具体而言, AGPCS-OIC基于粒球的多中心结构建模, 有效刻画类别内部的分布异质性, 并通过结构稀疏性拆分机制细化边界区域, 从而提升类内紧致性和类间可分性.此外, 引入粒球感知对比学习, 增强样本与类别结构的匹配性, 进一步提高模型在复杂分布下的判别能力与鲁棒性.

已知类别比例为25%时, 在BANKING、OOS、HWU64数据集上对AGPCS-OIC中的两个核心组件进行消融实验.设定如下变体.

1)w/o AGRL(without Adaptive Granular-Ball Re-presentation Learning).去除自适应粒球表征学习模块, 即不进行聚类与粒球感知对比学习, 仅采用交叉熵损失进行表示学习.

2)w/o PCS(without Pure Cluster Splitting).去除纯净簇拆分组件, 仅依赖粒球纯度进行划分.

3)w/o AGRL+PCS.同时移除自适应粒球表征学习模块和纯净簇拆分模块.

各变体在3个数据集上的消融实验结果如表7所示.表中黑体数字表示最优值.由表可看出, AGPCS-OIC在所有指标上均取得最优值, 由此验证各模块的协同贡献.w/o AGRL会导致F1-A指标降幅明显, 如在BANKING数据集上从76.71%降至68.59%, 下降8.12%, 表明自适应粒球结构对于构建有效语义边界至关重要.同时ACC指标降至78.88%, 验证其在提升分类稳健性方面的作用.

表7

Table 7

表7(Table 7)

表7 各变体消融实验结果 Table 7 Results of ablation experiments for each variant % 数据集 方法 F1-A ACC BANKING w/o AGRL 68.59 78.88 w/o PCS 65.27 85.28 w/o AGRL+PCS 71.05 77.82 AGPCS-OIC 76.71 86.30 OOS w/o AGRL 78.63 89.99 w/o PCS 62.25 88.94 w/o AGRL+PCS 74.58 83.86 AGPCS-OIC 82.14 92.65 HWU64 w/o AGRL 70.98 80.27 w/o PCS 64.15 84.82 w/o AGRL+PCS 65.71 67.10 AGPCS-OIC 74.46 85.32

表7 各变体消融实验结果 Table 7 Results of ablation experiments for each variant %

对于w/o PCS而言, 尽管类内结构已被粒球聚类捕捉, 但由于忽略对结构稀疏簇的进一步细化, 仍在多个数据集上出现性能下滑.如在OOS数据集上, F1-A指标从82.14%降至62.25%, 下降近20%, 说明纯净簇拆分能有效规避由松散结构导致的开放类误判, 提升边界判别精度.

更进一步地, 对于w/o AGRL+PCS而言, 整体性能进一步下降, 如在HWU64数据集上F1-A指标从74.46%降至65.71%, ACC指标从85.32%降至67.10%.这一现象表明, 缺乏粒球结构建模与结构敏感拆分机制, 模型将难以刻画类内异质性, 边界表征模糊, 导致在已知类判别和未知类排斥方面均失效.

为了评估关键超参数对方法性能的影响, 选择粒球纯净度阈值τ_p、粒球最小样本数阈值τ_n、粒球感知对比学习权重λ 及结构稀疏性拆分系数δ 进行参数敏感性实验, 所选数据集与设置分别为HWU64数据集(已知类别比例为75%)、HWU64数据集(已知类别比例为50%)、OOS数据集(已知类别比例为25%)、BANKING数据集(已知类别比例为25%).

在HWU64数据集(已知类别比例为75%)上, 设定粒球纯净度阈值τ_p=0.80, 0.85, 0.87, 0.90, 0.95, 0.97, 评估τ_p不同时方法性能的变化, 结果如表8所示.当τ_p=0.87时, AGPCS-OIC在4项指标上均达到最优值.这一结果表明, 适当提高纯净度阈值有助于过滤低质量粒球, 增强类别区分度, 若阈值过高, 则可能导致粒球数量不足、覆盖不足, 进而降低已知类的覆盖率和整体判别能力.

表8

Table 8

表8(Table 8)

表8 不同τp对方法性能的影响 Table 8 Effect of different τp on method performance τp F1-U/% F1-K/% F1-A/% ACC/% 0.80 72.59 85.10 84.85 81.88 0.85 72.56 85.25 84.99 81.97 0.87 72.78 85.37 85.11 82.16 0.90 72.39 85.28 85.01 82.06 0.95 72.33 84.06 83.83 81.78 0.97 72.33 84.06 83.83 81.78

表8 不同τp对方法性能的影响 Table 8 Effect of different τp on method performance

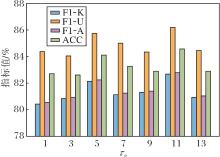
在HWU64数据集(已知类别比例为50%)上, 设定粒球最小样本数阈值τ_n=1, 3, …, 13, 不同τ_n对方法性能的影响如图2所示.由图可见, 当τ_n=11时, AGPCS-OIC在F1-U、F1-K、F1-A、ACC指标上均取得最优值.此外, 当τ_n=5时, AGPCS-OIC也取得相对较优的性能.然而, τ_n过小(如τ_n=1, 3)和τ_n过大均会导致性能下降, 这一结果说明:当τ_n设置过小时, 部分粒球仅由极少数样本构成, 结构稳定性差, 甚至可能由噪声或离群点构成, 若将这些粒球用于表征学习或判别边界构建, 容易导致模型过度拟合训练数据, 降低泛化性能; 当τ_n过大时, 虽可抑制噪声对粒球的影响, 但也可能忽略部分有意义的细粒度结构, 限制模型对复杂分布的适应能力.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 不同τn对方法性能的影响Fig.2 Effect of different τn on method performance

为了评估粒球感知对比学习在表征学习中的作用, 引入权重超参数λ , 用于控制粒球分类损失与对比学习损失在联合优化目标中的相对比例.在OOS数据集(已知类别比例为25%)上进行实验, 设定λ =0.1, 0.3, 0.5, 0.7, 0.9, 1.0, 评估λ 不同对方法性能的影响, 结果如表9所示.由表可见, 当λ =0.3时, AGPCS-OIC在多个指标上达到最优值.说明在该设定下, 分类损失与对比损失的协同优化最充分.粒球感知对比学习通过引入粒球中心作为结构锚点, 在保持类别区分性的同时提升语义表示的局部一致性.合理设置权重λ 能有效协调分类损失与对比损失之间的优化平衡, 进一步提升方法在开放意图分类任务中的表现与泛化性.

表9

Table 9

表9(Table 9)

表9 不同λ 对方法性能的影响 Table 9 Effect of different λ on method performance λ F1-U/% F1-K/% F1-A/% ACC/% 0.1 95.51 82.14 82.49 92.77 0.3 95.58 82.49 82.83 92.88 0.5 95.41 81.84 82.19 92.61 0.7 95.23 81.38 81.74 92.33 0.9 95.48 82.31 82.65 92.72 1.0 95.48 82.26 82.59 92.72

表9 不同λ 对方法性能的影响 Table 9 Effect of different λ on method performance

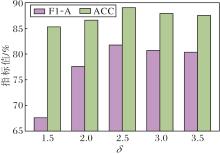
在BANKING数据集(已知类比例为25%)上, 设定结构稀疏性拆分系数δ =1.5, 2.0, …, 3.5, 不同δ 对方法性能的影响如图3所示.δ 表示粒球内最远样本距离与平均距离的比值, 用于度量粒球内部结构的离散程度.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同δ 对方法性能的影响Fig.3 Effect of different δ on method performance

由图3可见, 当δ =2.5时, AGPCS-OIC在F1-A和ACC指标上分别达到81.75%和89.03%, 取得最优值.合适的δ 值在粒球结构判别中具有良好的平衡性, 能有效缓解因“ 过拆分” 带来的粒球碎片化问题, 同时避免因“ 欠拆分” 造成的边界模糊现象, 因此可进一步提升类内一致性建模能力与开放类排斥能力.

为了验证AGPCS-OIC学习的粒球结构在语义空间中的可解释性, 从局部类内聚合性与全局类间可分性这2个角度进行可视化分析.

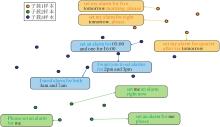
首先, 利用t-SNE将AGPCS-OIC在测试阶段提取的语义表示执行降维可视化.如图4所示, OOS数据集同一类别下的样本在特征空间中呈现出明显的多簇聚集结构, 说明存在内部语义子簇.相比传统的单质心建模策略, 本文引入的自适应粒球机制能更有效地捕捉这类内部异质性, 生成多个不同半径的子粒球, 实现对复杂类内结构的精细建模.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 “alarm” 类的3个子簇在特征空间中的分布Fig.4 Distribution of three subclusters of class “alarm” in feature space

进一步地, 将所有已知类别的粒球中心与样本表示统一投影至二维空间, 不同类别样本使用不同的颜色进行标记.

意图样本的t-SNE(t-Distributed Stochastic Neigh-bor Embedding)可视化结果如图5所示.由图可见, 同类样本在特征空间中大多呈现单簇或多簇结构性聚集, 表明模型能有效捕捉类内多样性结构.同时, 不同类别之间的粒球结构相互分离、边界清晰, 显示出良好的类间可分性.这一结果充分体现AGPCS-OIC在建模类内紧致性与类间判别性方面的性能.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 意图样本t-SNE可视化结果Fig.5 t-SNE visualization result of intent samples

上述结果直观验证粒球结构在特征空间中的有效性和可解释性, 为开放意图分类任务中的判别鲁棒性提供理论支持.