称FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统^[24], 其中, U为非空有限对象集, 称为论域, C为条件属性集, D={d}为决策属性, C∩ D=Ø , f ∶ U× C→ [0, 1], ∀ x∈ U, a∈ C, f(x, a)∈ [0, 1]表示对象x在条件属性a下的取值, g∶ U× D→ V_D, V_D为决策属性d的值域.使用P(U)表示U上经典子集全体, F(U)表示U上模糊集全体^[24].

∀ A⊆C, R_A为由A诱导的模糊关系, ∀ x∈ U, y∈ U, 若R_A满足

R_A(x, x)=1, R_A(x, y)=R_A(y, x),

称R_A为U上的模糊相似关系^[24].∀ x∈ U, y∈ U, 记

[x]_A(y)=R_A(x, y),

称[x]_A为x关于R_A的模糊信息粒.

定义1^[24] 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统,

U/D={D₁, D₂, …, D_r}

为U关于D的划分, R_C为由C诱导的模糊相似关系.∀ x∈ U, D_i∈ U/D, D_i的模糊决策如下所示:

D~i(x)= ∣[x]C⋂Di∣∣[x]C∣.

记

$\widetilde{D}=\left\{\widetilde{D}_{1}, \widetilde{D}_{2}, \cdots, \widetilde{D}_{r}\right\}$

为{D₁, D₂, …, D_r}上关于C的模糊决策粒覆盖.

定义2^[9] 设U为论域, R为U上的模糊相似关系.∀ X∈ F(U), ∀ x∈ U, X关于一系列模糊相似关系R_i(1≤ i≤ m)的乐观多粒度模糊下、上近似分别定义如下:

$\underline{\underset{i=1}{\overset{m}{\mathop{\sum }}}\, R_{i}^{O}}(X)(x)=\vee _{i=1}^{m}{{\wedge }_{y\in U}}((1-{{R}_{i}}(x, y))\vee X(y)) $

$\overline{\underset{i=1}{\overset{m}{\mathop{\sum }}}\, R_{i}^{O}}(X)(x)=\wedge _{i=1}^{m}{{\vee }_{y\in U}}({{R}_{i}}(x, y)\wedge X(y)) $

传统的多粒度模糊粗糙集通常依赖固定阈值定义属性子集上的模糊相似关系.然而, 由于不同属性的取值范围与数据分布存在显著差异, 统一阈值难以适配所有属性, 容易导致相似性度量失真.为此, 本文借鉴文献[20]和文献[23]的思路, 将Hyndman等^[25]提出的基于线性插值计算分位数的方法引入模糊决策信息系统, 设置可调节的位置修正项, 计算任意属性下对象间距离顺序统计量的第k分位数, 并将其作为该属性的自适应阈值.基于此阈值定义任意属性子集下的模糊相似关系及模糊信息粒, 进而构建基于自适应阈值的乐观多粒度模糊决策粗糙集模型.

给定模糊决策信息系统FDS=(U, C∪ D, f, V_D, g), ∀ a∈ C, x_i∈ U, x_j∈ U, 对象x_i、x_j在属性a下的距离定义如下:

${{d}_{a}}({{x}_{i}}, {{x}_{j}})=\left| f({{x}_{i}}, a)-f({{x}_{j}}, a) \right|$.

记|U|=n, 则属性a下对象间的距离构成一个n阶矩阵, 记为

M_a= [da(xi, xj)]n×n.

由于

d_a(x_i, x_i)=0, d_a(x_i, x_j)=d_a(x_j, x_i),

因此, 仅需考虑该距离矩阵M_a不含主对角线元素的上三角部分, 记为 Ma+, 则

Ma+=

0da(x1, x2)…da(x1, xn-1)da(x1, xn)00…da(x2, xn-1)da(x2, xn)︙︙︙︙00…0da(xn-1, xn)00…00n×n.

显然, 矩阵 Ma+中有 12n(n-1)个距离值, 按行展开, 记为d_a(x_i, x_j), i=1, 2, …, n-1, j=i+1, i+2, …, n.

采用统计学中由样本建立顺序统计量的方法, 将上述 12n(n-1)个距离值按照从小到大的顺序排列, 记为 da(1), da(2), …, da(t), 满足

da(1)≤ da(2)≤ …≤ da(t),

da(i)∈ {d_a(x_i, x_j)∶ i=1, 2, …, n-1, j=i+1, i+2, …, n}, t= 12n(n-1).

下面利用分位数引入任意属性的阈值.

定义3 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统, n=|U|, ∀ a∈ C, Ma+为属性a的严格上三角距离矩阵, 按行展开距离数据d_a(x_i, x_j), i=1, 2, …, n-1, j=i+1, i+2, …, n, 按照从小到大的顺序排列为 da(1), da(2), …, da(t), t= 12n(n-1).给定分位数参数k∈ (0, 1), 属性a的阈值 δak定义为该属性下距离值顺序统计量的第k分位数, 即

$\delta _{a}^{k}=d_{a}^{(\left\lfloor tk+m \right\rfloor)}+(tk+m-\left\lfloor tk+m \right\rfloor)(d_{a}^{(\left\lfloor tk+m \right\rfloor +1)}-d_{a}^{(\left\lfloor tk+m \right\rfloor)}) $, (1)

其中, ⌊· 」表示向下取整, m∈ [0, 1]表示位置修正项.记

mδCk={δak∶ a∈ C},

称为条件属性集C在分位数参数k下的自适应阈值集合.

式(1)在文献[25]的基础上将位置修正项m的取值范围由全体实数限制在区间[0, 1]内, 使 δak限制在 da(⌊tk」)、 da(⌊tk+1」)和 da(⌊tk+2」)之间.具体而言, 当

0≤ tk-⌊tk」≤ 1-m

时,

da(⌊tk」)≤ δak≤ da(⌊tk+1」),

当

1-m< tk-⌊tk」< 1

时,

da(⌊tk」+1)< δak< da(⌊tk」+2),

这样既能有效约束分位位置, 又能保证阈值 δak随分位数参数k变化的平滑性.

特别地, 当m=0.5时, 属性a的阈值

δak= da(⌊tk+0.5」)+(tk+0.5-⌊tk+0.5」)(da(⌊tk+0.5」+1)- da(⌊tk+0.5」)).

该式为文献[25]中关于分位数的第5个公式, 满足分位数的所有性质.

分位数是一个位置指标, 针对每个属性下对象间的距离值, 采用线性插值法计算分位数, 以此作为该属性的阈值, 使得至少100k%的对象关于单属性的距离值小于等于 δak.该方法衡量对象在该属性下的距离值顺序统计量中的相对位置, 而不受数据绝对大小和量纲的影响.

定义4 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统, ∀ a∈ C, k∈ (0, 1), δak∈ m δCk, ∀ x∈ U, y∈ U, 属性a的模糊相似关系定义如下:

Rak(x, y)= exp(-da(x, y)22σ2), da(x, y)≤δak0, 其它(2)

其中σ 为高斯核宽度.∀ A⊆C, 定义

RAk= ∩a∈ARak,

则 RAk为属性子集A的模糊相似关系.∀ y∈ U, 模糊信息粒 [x]Ak满足

[x]Ak(y)= RAk(x, y).

∀ D_i∈ U/D, x∈ U, D_i的模糊决策为:

D~i(x)= ∣[x]Ck⋂Di∣∣[x]Ck∣.(3)

性质1 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统, ∀ A⊆C, A₁⊆C, A₂⊆C, k∈ (0, 1), k₁∈ (0, 1), k₂∈ (0, 1), ∀ a∈ C, x∈ U, 下列性质成立:

1)k₁≤ k₂ ⇒ δak1≤ δak2,

2)k₁≤ k₂ ⇒ RAk1⊆ RAk2, [x]Ak1⊆ [x]Ak2,

3)A₁⊆A₂ ⇒ RA2k⊆ RA1k, [x]A2k⊆ [x]A1k.

证明 先证1).∀ a∈ C, k₁∈ (0, 1), k₂∈ (0, 1), k₁≤ k₂, 有

t· k₁+m≤ t· k₂+m

且

⌊t· k₁+m」≤ ⌊t· k₂+m」,

则

t· k₁+m-⌊t· k₁+m」≤ t· k₂+m-⌊t· k₂+m」.

由定义3知

$\begin{array}{l} d_{a}^{\left(\left\lfloor t k_{1}+m\right\rfloor\right)}+ \\ \quad\left(t k_{1}+m-\left\lfloor t k_{1}+m\right\rfloor\right)\left(d_{a}^{\left(\left\lfloor t k_{1}+m\right\rfloor+1\right)}-d_{a}^{\left(\left\lfloor t k_{1}+m\right\rfloor\right)}\right) \leqslant \\ d_{a}^{\left(\left\lfloor t k_{2}+m\right\rfloor\right)}+ \\ \quad\left(t k_{2}+m-\left\lfloor t k_{2}+m\right\rfloor\right)\left(d_{a}^{\left(\left\lfloor t k_{2}+m\right\rfloor+1\right)}-d_{a}^{\left(\left\lfloor t k_{2}+m\right\rfloor\right)}\right) \end{array}$

即 δak1≤ δak2.

再证2).设k₁≤ k₂.∀ a∈ A⊆C, 由1)知 δak1≤ δak2.∀ x∈ U, y∈ U, 由式(2)知, 若

d_a(x, y)≤ δak1,

有

$R_{a}^{{{k}_{1}}}(x, y)=\exp \left( -\frac{{{d}_{a}}{{(x, y)}^{2}}}{2{{\sigma }^{2}}} \right)=R_{a}^{{{k}_{2}}}(x, y) $;

若

δak1< d_a(x, y)≤ δak2,

有

$R_{a}^{{{k}_{1}}}(x, y)=0\le \exp \left( -\frac{{{d}_{a}}{{(x, y)}^{2}}}{2{{\sigma }^{2}}} \right)=R_{a}^{{{k}_{2}}}(x, y) $;

若

δak2< d_a(x, y),

有

Rak1(x, y)=0= Rak2(x, y).

由x、y的任意性得

Rak1⊆ Rak2,

由a的任意性知

RAk1⊆ RAk2.

进一步地, ∀ x∈ U, y∈ U,

[x]Ak1(y)= RAk1(x, y)≤ RAk2(x, y)= [x]Ak2(y),

由x的任意性得

[x]Ak1⊆ [x]Ak2.

最后证3).设A₁⊆A₂, 由定义4知,

$\begin{array}{c} R_{A_{2}}^{k}=\bigcap_{a \in A_{2}} R_{a}^{k}=\left(\bigcap_{a \in A_{1}} R_{a}^{k}\right) \cap\left(\bigcap_{a \in A_{2}-A_{1}} R_{a}^{k}\right)= \\ R_{A_{1}}^{k} \cap R_{A_{2}-A_{1}}^{k} \subseteq R_{A_{1}}^{k} . \end{array}$

∀ x∈ U, y∈ U,

[x]A2k(y)= RA2k(x, y)≤ RA1k(x, y)= [x]A1k(y),

故由x的任意性知

[x]A2k⊆ [x]A1k.

定义5 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统,

$\begin{array}{l} \mathcal{A}=\left\{A_{1}, A_{2}, \cdots, A_{m}\right\} \subseteq \mathscr{P}(C), \\ \widetilde{D}=\left\{\widetilde{D}_{1}, \widetilde{D}_{2}, \cdots, \widetilde{D}_{r}\right\} \end{array}$

为U上的模糊决策粒覆盖, k∈ (0, 1).∀ B⊆A, D~关于条件属性子集族B的乐观多粒度模糊决策下、上近似分别定义如下:

$\begin{array}{l} \underline{R}_{\mathcal{B}}^{O, k}(\widetilde{D})=\left\{\underline{R}_{\mathcal{B}}^{O, k}\left(\widetilde{D}_{1}\right), \underline{R}_{\mathcal{B}}^{O, k}\left(\widetilde{D}_{2}\right), \cdots, \underline{R}_{\mathcal{B}}^{O, k}\left(\widetilde{D}_{r}\right)\right\}, \\ \bar{R}_{\mathcal{B}}^{O, k}(\widetilde{D})=\left\{\bar{R}_{\mathcal{B}}^{O, k}\left(\widetilde{D}_{1}\right), \bar{R}_{\mathcal{B}}^{O, k}\left(\widetilde{D}_{2}\right), \cdots, \bar{R}_{\mathcal{B}}^{O, k}\left(\widetilde{D}_{r}\right)\right\} . \end{array}$

其中, D~j关于条件属性子集族B的乐观多粒度模糊下、上近似分别定义如下:

$\underline{R}_{\mathcal{B}}^{o, k}\left(\widetilde{D}_{j}\right)(x)=\bigvee_{A_{i} \in \mathcal{B}} \bigwedge_{y \in U}\left(\left(1-[x]_{A_{i}}^{k}(y)\right) \vee \widetilde{D}_{j}(y)\right), $(4)

$ \bar{R}_{\mathcal{B}}^{o, k}\left(\widetilde{D}_{j}\right)(x)=\bigwedge_{A_{i} \in \mathcal{B}} \bigvee_{y \in U}\left([x]_{A_{i}}^{k}(y) \wedge \widetilde{D}_{j}(y)\right) . $ (5)

D~关于条件属性子集族B的乐观多粒度模糊正域$ \operatorname{POS}_{\mathcal{B}}^{O, k}(\widetilde{D}) $、边界域$ B N D_{\mathcal {B}}^{O, k}(\widetilde{D}) $分别定义如下:

$ \begin{array}{l} \operatorname{POS}_{\mathcal{B}}^{O, k}(\widetilde{D})=\bigcup_{j=1}^{r} \underline{R}_{\mathcal{B}}^{O, k}\left(\widetilde{D}_{j}\right), \\ \operatorname{BND}_{\mathcal{B}}^{O, k}(\widetilde{D})=\bigcup_{j=1}^{r} \bar{R}_{\mathcal{B}}^{O, k}\left(\widetilde{D}_{j}\right)-\bigcup_{j=1}^{r} \underline{R}_{\mathcal{B}}^{O, k}\left(\widetilde{D}_{j}\right) . \end{array} $

D~关于B的乐观多粒度模糊精度$ \alpha_{\mathcal{B}}^{O, k}(\widetilde{D}) $和乐观多粒度模糊粗糙度$ \rho_{\mathcal{B}}^{o, k}(\widetilde{D}) $分别定义如下:

$ \alpha_{\mathcal{B}}^{O, k}(\widetilde{D})=\frac{\left|\underline{R}_{\mathcal{B}}^{O, k}(\widetilde{D})\right|}{\left|\overline{R_{\mathcal{B}}^{O, k}}(\widetilde{D})\right|}=\frac{\sum_{j=1}^{r} \sum_{x \in U} \underline{R}_{\mathcal{B}}^{O, k}\left(\widetilde{D}_{j}\right)(x)}{\sum_{j=1}^{r} \sum_{x \in U} \bar{R}_{\mathcal{B}}^{O, k}\left(\widetilde{D}_{j}\right)(x)}, $ (6)

$ \rho_{\mathcal{B}}^{O, k}(\widetilde{D})=1-\frac{\left|\underline{R}_{\mathcal{B}}^{O, k}(\widetilde{D})\right|}{\left|\bar{R}_{\mathcal{B}}^{O, k}(\widetilde{D})\right|}=\frac{\sum_{x \in U} B N D_{\mathcal{B}}^{O, k}(\widetilde{D})(x)}{\sum_{j=1}^{r} \sum_{x \in U} \bar{R}_{\mathcal{B}}^{O, k}\left(\widetilde{D}_{j}\right)(x)} . $ (7)

性质2 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统,

A={A₁, A₂, …, A_m}⊆P(C),

k∈ (0, 1), ∀ B⊆A, C⊆A, D~j∈ D~, 下列性质成立:

1) R¯BO, k(D~j)⊆ D~j⊆ R¯BO, k(D~j),

2) R¯BO, k(D~j)= ∨Ai∈BR¯Aik(D~j),

R¯BO, k(D~j)= ∧Ai∈BR¯Aik(D~j),

3)C⊆B⇒ R¯CO, k(D~j)R¯BO, k(D~j),

R¯BO, k(D~j)⊆ R¯CO, k(D~j),

4)A₁⊆A₂⊆…⊆A_m⇒ R¯BO, k(D~j)= R¯AmO, k(D~j),

R¯BO, k(D~j)= R¯AmO, k(D~j),

其中,

$\begin{align} & \underline{R}_{{{A}_{i}}}^{k}({{{\tilde{D}}}_{j}})={{\wedge }_{y\in U}}((1-[x]_{{{A}_{i}}}^{k}(y))\vee {{{\tilde{D}}}_{j}}(y), \ \\ & \overline{R}_{{{A}_{i}}}^{k}({{{\tilde{D}}}_{j}})={{\vee }_{y\in U}}([x]_{{{A}_{i}}}^{k}(y)\wedge {{{\tilde{D}}}_{j}}(y)) \\ \end{align}$

证明 由式(4)和式(5)可证2)成立, 由2)可证3)成立, 由性质1中3)和性质2中2)可证4)成立.下证1)成立.∀ A_i∈ B, x∈ U, y∈ U, 由定义4知

[x]Aik(x)=1,

则有

$\begin{align} & {{\wedge }_{y\in U}}((1-[x]_{{{A}_{i}}}^{k}(y))\vee {{{\tilde{D}}}_{j}}(y))= \\ & \{{{\wedge }_{y\ne x}}((1-[x]_{{{A}_{i}}}^{k}(y))\vee {{{\tilde{D}}}_{j}}(y))\}\wedge {{{\tilde{D}}}_{j}}(x)\le {{{\tilde{D}}}_{j}}(x) \\ \end{align}$

故由A_i的任意性得

$\begin{array}{l} \underline{R}_{\mathcal{B}}^{o, k}\left(\widetilde{D}_{j}\right)(x)= \\ \quad \bigvee_{A_{i} \in \mathcal{B}} \bigwedge_{y \in U}\left(\left(1-[x]_{A_{i}}^{k}(y)\right) \vee \widetilde{D}_{j}(y)\right) \leqslant \\ \quad \widetilde{D}_{j}(x)\end{array}$

由x的任意性即得

R¯BO, k(D~j)⊆ D~j.

类似可证

D~j⊆ R¯BO, k(D~j).

性质3 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统,

A={A₁, A₂, …, A_m}⊆P(C),

k∈ (0, 1), ∀ C⊆A, B⊆A, 下列性质成立:

1)0≤ αBO, k(D~)≤ 1, 0≤ ρBO, k(D~)≤ 1,

2)C⊆B ⇒ αCO, k(D~)≤ αBO, k(D~),

ρBO, k(D~)≤ ρCO, k(D~),

3)A₁⊆A₂⊆…⊆A_m⇒ αAO, k(D~)= αAmO, k(D~),

βAO, k(D~)= βAmO, k(D~).

证明 由性质2可证结论成立.

Wang等^[14]应用决策的下、上近似及边界信息提出基于邻域自信息的属性约简方法.基于此方法, 本节在模糊决策信息系统上, 利用乐观多粒度模糊决策下、上近似及其边界域, 提出模糊自信息(FSI), 并应用其讨论乐观多粒度模糊决策粗糙集上的属性约简方法.

定义6 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统,

A={A₁, A₂, …, A_m}⊆P(C),

k∈ (0, 1), ∀ B⊆A, D~关于B的模糊自信息定义如下:

FSIBO, k(D~)=- ρBO, k(D~)ln αBO, k(D~).(8)

性质4 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统,

A={A₁, A₂, …, A_m}⊆P(C),

k∈ (0, 1), ∀ C⊆A, B⊆A, 下列性质成立:

1)0≤ FSIBO, k(D~)< +$ \infty$, 当 αBO, k(D~)=1时,

FSIBO, k(D~)=0,

当 αBO, k(D~)→ 0时,

FSIBO, k(D~)→ +$\infty$,

2)C⊆B⇒ FSIBO, k(D~)≤ FSICO, k(D~),

3)A₁⊆A₂⊆…⊆A_m⇒

FSIAO, k(D~)= FSIAmO, k(D~).

证明 由性质3中1)与3)可证1)与3)成立.下证2)成立.设C⊆B, 由性质3中3)知

αCO, k(D~)≤ αBO, k(D~),

则

0≤ -ln αBO, k(D~)≤ -ln αCO, k(D~),

0≤ ρBO, k(D~)≤ ρCO, k(D~)≤ 1,

因此

FSIBO, k(D~)≤ FSICO, k(D~).

定义7 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统,

A={A₁, A₂, …, A_m}⊆P(C),

k∈ (0, 1), ∀ ε ≥ 0, A∈ A, 若

FSIA-AO, k(D~)- FSIAO, k(D~)≤ ε ,

称A在A中是ε -不必要的, 否则, 称A在A中是ε -必要的.∀ B⊆A, 若

FSIBO, k(D~)- FSIAO, k(D~)≤ ε ,

且∀ A∈ B,

FSIB-AO, k(D~)- FSIBO, k(D~)> ε ,

称B是A的ε -约简.记{B_i∶ 1≤ i≤ t}为A的所有ε -约简集.若

A∈ ⋂i=1tB_i,

称A为ε -核心属性集, 并记

Core_ε (A)= ⋂i=1tB_i.

定义8 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统,

A={A₁, A₂, …, A_m}⊆P(C),

k∈ (0, 1), ∀ B⊆A, A∈ B, A关于B和 D~的内重要度定义如下:

Sig_inter(A, B, D~)= FSIB-{A}O, k(D~)- FSIBO, k(D~).(9)

∀ A∈ A-B, A关于B和 D~的外重要度定义如下:

Sig_outer(A, B, D~)= FSIBO, k(D~)- FSIB⋃{A}O, k(D~).(10)

定理1 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统,

A={A₁, A₂, …, A_m}⊆P(C),

k∈ (0, 1), ε ≥ 0, 下列结论成立:

1)Core_ε (A)={A∈ A∶ FSIA-AO, k(D~)- FSIAO, k(D~)> ε},

2)A∈ Core_ε (A)⇔ Sig_inter(A, A, D~)> ε .

证明 由1)和式(9)可证2)成立.下证1)成立.记

L={A∈ A∶ FSIA-AO, k(D~)- FSIAO, k(D~)> ε},

∀ A∈ Core_ε (A), 若

FSIA-AO, k(D~)- FSIAO, k(D~)≤ ε ,

则∃B⊆A-{A},

FSIBO, k(D~)- FSIAO, k(D~)≤ ε ,

且∀ B∈ B,

FSIB-BO, k(D~)- FSIAO, k(D~)> ε ,

即存在ε -约简集B且A∉B, 这与A∈ Core_ε (A)矛盾.于是

FSIA-AO, k(D~)- FSIAO, k(D~)> ε ,

即A∈ L.由A的任意性知

Core_ε (A)⊆L .

反之, ∀ A∈ L, 则

FSIA-AO, k(D~)- FSIAO, k(D~)> ε .

若存在ε -约简集B使得A∉B, 则

FSIBO, k(D~)- FSIAO, k(D~)≤ ε .

由

B⊆A-{A}⊆A

及性质3中2)可得

FSIA-AO, k(D~)- FSIAO, k(D~)≤ FSIBO, k(D~)- FSIAO, k(D~)≤ ε ,

这与A∈ L矛盾, 故A∈ Core_ε (A).由A的任意性知

L⊆Core_ε (A).

综上可知,

Core_ε (A)=L .

定理2 设FDS=(U, C∪ D, f, V_D, g)为模糊决策信息系统,

A={A₁, A₂, …, A_m}⊆P(C),

k∈ (0, 1), ε ≥ 0, ∀ A∈ A,

A在A中是ε -不必要的⇔

Sig_outer(A, A-{A}, D~)≤ ε .

证明 由定义7和式(10)可证.

根据定理1和定理2可给出基于模糊自信息的属性约简算法(FSIAR), 具体过程步骤如算法1所示.

算法1 FSIAR

输入 模糊决策信息系统

FDS=(U, C∪ D, f, V_D, g),

A={A₁, A₂, …, A_m},

m∈ [0, 1], k∈ (0, 1), σ > 0, ε ≥ 0

输出 约简集B

step 1 设置初始值B← Ø ;

step 2 ∀ a∈ C, 根据式(1)和式(2)计算属性a的阈值 δak和模糊相似关系 Rak, ∀ A_i∈ A, 计算模糊相似关系 RAik和模糊信息粒 [x]Aik;

step 3 根据式(3)计算模糊决策粒覆盖

D~={D~1, D~2, … D~r};

step 4 ∀ A_i∈ A, D~j∈ D~, 计算单粒度模糊下、上近似 R¯Aik(D~j)和 R¯Aik(D~j), 根据性质2中2)计算 R¯A-AiO, k(D~)和 R¯A-AiO, k(D~), 根据式(6)和式(7)计算乐观多粒度模糊精度 αA-AiO, k(D~)和乐观多粒度模糊粗糙度 ρA-AiO, k(D~), 并根据式(8)计算 FSIA-AiO, k(D~)和 FSIAO, k(D~);

step 5 根据式(9)计算Sig_inter(A_i, A, D~), 若Sig_inter(A_i, A, D~)> ε , 则B← B∪ {A_i};

step 6 根据式(8)计算 FSIBO, k(D~), 若

FSIBO, k(D~)- FSIAO, k(D~)≤ ε ,

执行step 8, 否则执行step 7;

step 7 ∀ A∈ A-B, 根据式(10)计算Sig_outer(A, B, D~), 若

$\begin{array}{l} \operatorname{Sig}_{\text {outer }}(A, \mathcal{B}, \widetilde{D})= \\ \quad \max \left\{\operatorname{Sig}_{\text {outer }}(A, \mathcal{B}, \widetilde{D}): A \in A-B\right\}, \end{array}$

则

B← B∪ {A},

执行step 6;

step 8 输出约简集B.

为了验证FSIAR的有效性, 从UCI数据库上选取10个数据集进行实验, 实例数从70到1 482, 属性数从6到205, 具体信息如表1所示.

表1

Table 1

表1(Table 1)

表1 数据集信息 Table 1 Dataset information 名称 实例数 属性数 类别数 Ionosphere 351 34 2 Divorce Predictors 170 54 2 Wpbc 198 33 2 Lymphography 1482 19 4 Wine 178 13 3 Sonar 208 60 2 SCADI 70 205 7 Dermatology 366 34 6 Wbc 699 9 2 Maternal Health Risk 1013 6 3

表1 数据集信息 Table 1 Dataset information

由于部分数据存在缺失, 实验前对缺失数据运用均值法进行填充, 并应用最大最小归一化方法对数据进行归一化处理^[26], 得到模糊决策信息系统.

为了便于与其它属性约简算法对比, 本文将单属性作为一个属性子集进行实验^[5].实验中对所有数据集采用十折交叉验证, 使用CART(Classification and Regression Trees)和KNN(k-Nearest Neighbor)(K=3)两种经典分类器对属性约简算法的分类性能进行评估^[20].

4.1 参数分析

FSIAR含位置修正项m、分位数参数k、高斯核宽度σ 和约简参数ε , 其不同取值将对实验结果产生一定影响.为了分析各数据集上不同参数对约简结果的影响, 将高斯核宽度σ 设置为1^[27], m以0.1步长在区间[0, 1]内间隔取值, k以0.1步长在[0.1, 0.9]内间隔取值, ε 以0.005步长在[0, 0.05]内间隔取值.首先分析m取不同值时在各数据集上获得的最高分类精度和选取的属性数.

为了直观展示这一现象, 在Ionosphere、Divorce Predictors数据集上, 分别采用CART、KNN分类器, 不同m值对应的最高分类精度及选取的属性数如表2所示, 其余数据集结果类似.

表2

Table 2

表2(Table 2)

表2 m不同时2个数据集上的最高分类精度与选取的属性数 Table 2 Highest classification accuracy and the number of selected attributes under different m on 2 datasets m Ionosphere Divorce Predictors CART分类器 KNN分类器 CART分类器 KNN分类器 分类精度/% 属性数 分类精度/% 属性数 分类精度/% 属性数 分类精度/% 属性数 0 93.74 6 92.57 6 99.41 7 98.82 5 0.1 94.57 7 92.31 7 99.41 7 98.82 5 0.2 94.57 7 92.57 6 99.41 7 98.82 5 0.3 94.57 12 91.75 8 99.41 7 98.82 5 0.4 94.57 7 92.57 6 98.82 8 98.82 5 0.5 94.57 7 92.57 6 99.41 7 98.82 5 0.6 94.57 7 92.57 6 99.41 7 98.82 5 0.7 94.57 7 92.57 6 98.82 8 98.82 5 0.8 94.57 7 91.75 8 99.41 7 98.82 5 0.9 94.57 7 92.57 6 99.41 7 98.82 5 1.0 93.74 6 92.57 6 99.41 7 98.82 5

表2 m不同时2个数据集上的最高分类精度与选取的属性数 Table 2 Highest classification accuracy and the number of selected attributes under different m on 2 datasets

由表2可知, 不同m值下的分类精度差异较小, 表明FSIAR对[0, 1]区间上m的选择具有较强的鲁棒性.当m=0.5时, 式(1)满足分位数的所有性质, 故本文在后续实验中将位置修正项m设为0.5.在此设定下, 进一步分析分位数参数k、约简参数ε 对分类精度的影响, 在不同分位数参数k和约简参数ε 下, 在10个数据集上采用CART分类器得到的分类精度变化趋势如图1所示, 采用KNN分类器得到的曲面图与CART分类器大致相同.

图1

Fig.1

	Figure Option ViewDownloadNew Window
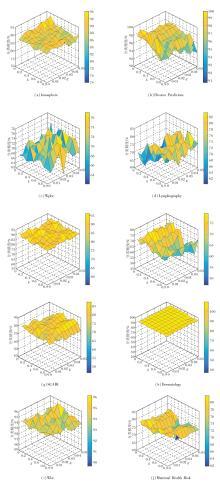	图1 不同k和ε 下CART分类器在10个数据集上的分类精度曲面图Fig.1 CART classification accuracy for 10 datasets under different parameters k and ε

由图1可知, 随着参数的变化, CART分类器分类精度不同.10个数据集上两个分类器分类精度最高时选择的分位数参数和约简参数取值组合如表3所示.

表3

Table 3

表3(Table 3)

表3 针对2个分类器选择的参数取值组合 Table 3 Parameter value combinations selected under two classifiers 数据集 CART KNN k ε k ε Ionosphere 0.1 0.050 0.3 0.040 Divorce Predictors 0.1 0.005 0.1 0.015 Wpbc 0.6 0.020 0.8 0.035 Lymphography 0.7 0.045 0.5 0.000 Wine 0.3 0.020 0.1 0.020 Sonar 0.7 0.010 0.8 0.000 SCADI 0.7 0.040 0.6 0.035 Dermatology 0.6 0.035 0.2 0.030 Wbc 0.3 0.045 0.2 0.000 Maternal Health Risk 0.6 0.000 0.2 0.045

表3 针对2个分类器选择的参数取值组合 Table 3 Parameter value combinations selected under two classifiers

4.2 对比实验

实验选取文献[5]方法、OMGE^[13]、PMGE^[13]、FRUAR^[20]这4种属性约简算法作为对比算法.各算法在10个数据集上约简后选取的属性数如表4所示, 表中黑体数字表示各数据集上基于CART分类器选择的最少属性数, 斜体数字表示各数据集上基于KNN分类器选择的最少属性数.由表可知, 在CART分类器上, FSIAR在5个数据集上选取的属性数最少, 文献[5]方法和FRUAR在3个数据集上选取的属性数最少, PMGE在2个数据集上选取的属性数最少.在KNN分类器上, FSIAR在6个数据集上选取的属性数最少, 文献[5]方法和FRUAR在2个数据集上选取的属性数最少, OMGE和PMGE在1个数据集上选取的属性数最少.综上所述, FSIAR在多个数据集上表现出良好的约简效果.

表4

Table 4

表4(Table 4)

表4 各算法选取的属性数对比 Table 4 Comparison of the number of attributes selected by different algorithms 数据集 原始数据 文献[5]方法 OMGE PMGE FRUAR FSIAR CART KNN CART KNN CART KNN CART KNN CART KNN Ionosphere 34 14 14 22 19 16 13 30 33 7 6 Divorce predictors 54 6 6 52 52 8 9 33 13 7 5 Wpbc 33 14 14 11 12 8 7 2 2 16 12 Lymphography 19 18 18 10 17 9 12 10 12 7 5 Wine 13 7 7 11 12 7 7 2 2 10 8 Sonar 60 20 20 16 7 8 9 25 39 20 21 SCADI 205 8 8 13 13 11 13 15 15 19 22 Dermatology 34 26 26 33 33 13 13 32 33 13 13 Wbc 9 7 7 9 9 9 9 8 8 6 7 Maternal Health Risk 6 5 5 6 6 6 6 5 5 5 4

表4 各算法选取的属性数对比 Table 4 Comparison of the number of attributes selected by different algorithms

原始数据及各算法对表4所得约简结果在CART和KNN分类器下的分类精度如表5和表6所示, 表中黑体数字表示最优值.由表可知, 在CART分类器下, FSIAR在9个数据集上取得最高分类精度, 仅在Wpbc数据集上次于OMGE.在KNN分类器下, FSIAR在10个数据集上均获得最高分类精度.

表5

Table 5

表5(Table 5)

表5 CART分类器下各算法的分类精度对比 Table 5 Comparison of classification accuracy among different algorithms under CART classifier % 数据集 原始数据 文献[5]方法 OMGE PMGE FRUAR FSIAR Ionosphere 86.90 89.76 90.86 90.07 89.47 94.57 Divorce predictors 95.29 96.47 95.88 95.88 98.82 99.41 Wpbc 69.24 73.63 76.89 73.74 76.79 76.45 Lymphography 74.19 75.00 79.00 79.19 81.76 82.43 Wine 87.58 88.24 91.57 93.24 92.75 94.38 Sonar 68.31 70.62 76.40 70.69 75.50 77.88 SCADI 74.29 78.57 82.86 77.14 85.71 85.71 Dermatology 93.15 95.07 93.15 78.44 96.45 96.73 Wbc 93.42 93.70 93.42 93.42 94.28 95.85 Maternal Health Risk 79.19 79.48 79.19 79.19 79.67 81.07

表5 CART分类器下各算法的分类精度对比 Table 5 Comparison of classification accuracy among different algorithms under CART classifier %

表6

Table 6

表6(Table 6)

表6 KNN分类器下各算法的分类精度对比 Table 6 Comparison of classification accuracy among different algorithms under KNN classifier % 数据集 原始数据 文献[5]方法 OMGE PMGE FRUAR FSIAR Ionosphere 84.34 88.04 87.17 87.75 83.76 92.57 Divorce Predictors 97.65 96.47 97.65 97.65 97.65 98.82 Wpbc 71.66 78.32 75.29 79.95 74.22 80.92 Lymphography 79.45 74.29 82.43 80.38 81.05 83.76 Wine 94.93 95.00 96.67 96.60 95.51 98.33 Sonar 82.31 79.33 75.86 72.07 85.07 87.55 SCADI 71.67 82.86 80.00 74.29 72.86 85.71 Dermatology 80.00 96.44 95.61 82.48 88.50 98.65 Wbc 95.86 95.85 95.86 95.86 96.28 96.86 Maternal Health Risk 68.74 71.80 68.74 68.74 69.13 75.55

表6 KNN分类器下各算法的分类精度对比 Table 6 Comparison of classification accuracy among different algorithms under KNN classifier %

本文提出基于自适应阈值的乐观多粒度模糊决策粗糙集, 并探讨基于模糊自信息的属性约简.首先, 针对多粒度模糊粗糙集上基于固定阈值构造模糊关系的问题, 采用分位数定义单属性的阈值, 构造属性子集下基于自适应阈值的模糊相似关系.然后, 在属性子集族上提出基于自适应阈值的乐观多粒度模糊决策粗糙集.利用乐观多粒度模糊决策下、上近似及边界域的信息, 提出模糊自信息(FSI), 给出基于模糊自信息的属性约简算法(FSIAR).实验表明, FSIAR在多个数据集上可有效降低原始属性集维数并提升分类精度.今后将考虑在不完备数据集上多粒度模糊粗糙集的属性约简方法.

本文责任编委 张燕平

Recommended by Associate Editor ZHANG Yanping