引用本文
周新宇, 蒋金峰, 高卫峰, 王晖, 彭虎. 动态精英学习的约束差分进化算法. 模式识别与人工智能, 2025,38(9): 820-836
ZHOU Xinyu, JIANG Jinfeng, GAO Weifeng, WANG Hui, PENG Hu. Constrained Differential Evolution Algorithm with Dynamic Elite Learning. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2025,38(9): 820-836.  
Doi: 10.16451/j.cnki.issn1003-6059.202509005
Permissions
Copyright©2025, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
动态精英学习的约束差分进化算法
周新宇1,2, 蒋金峰1, 高卫峰3, 王晖4, 彭虎5
1.江西师范大学 人工智能学院 南昌 330022
2.江西师范大学 智能信息处理与情感计算江西省重点实验室 南昌 330022
3.西安电子科技大学 数学与统计学院 西安 710071
4.江西水利电力大学 信息工程学院 南昌 330099
5.九江学院 计算机与大数据科学学院 九江 332005
通信作者:

彭 虎,博士,教授,主要研究方向为进化计算及其应用.E-mail:hu_peng@whu.edu.cn.

作者简介:

周新宇,博士,副教授,主要研究方向为智能计算.E-mail:xyzhou@jxnu.edu.cn.

蒋金峰,硕士,主要研究方向为约束进化优化.E-mail:aisie_jiang@163.com.

高卫峰,博士,教授,主要研究方向为智能计算、深度学习等.E-mail:gaoweifeng2004@126.com.

王 晖,博士,教授,主要研究方向为智能计算.E-mail:huiwang@whu.edu.cn.

收稿日期: 2025-08-20 接受日期: 2025-09-21
资助项目: 国家自然科学基金项目(No.62366022,62276202,62166027,62266024)、江西省自然科学基金项目(No.20232BAB202048)、江西省自然科学基金杰出青年基金项目(No.20212ACB212004)资助
摘要

约束差分进化算法是求解约束优化问题的一种有效手段.然而,现有相关工作主要聚焦在约束处理技术方面,对差分进化算法本身关注较少,导致存在勘探和开采能力不均衡、可行解的后代个体存活率较低等问题.为此,文中提出动态精英学习的约束差分进化算法,将种群中个体划分为普通可行解、精英可行解、不可行解,分别为这三类个体采用个性化的变异算子,平衡算法的勘探和开采能力.同时,引入精英可行解,改进经典的变异算子,提高可行解的后代个体存活率.针对不可行解的特点,设计微调的可行性规则,作为约束处理技术,较好地引导种群进入可行域.在CEC2006、CEC2010、CEC2017测试集和3个实际工程优化问题上的大量实验表明文中算法性能较优.

关键词: 约束优化; 差分进化; 可行性规则; 可行解; 不可行解
中图分类号:TP301
Constrained Differential Evolution Algorithm with Dynamic Elite Learning
ZHOU Xinyu1,2, JIANG Jinfeng1, GAO Weifeng3, WANG Hui4, PENG Hu5
1. School of Artificial Intelligence, Jiangxi Normal University, Nanchang 330022
2. Key Laboratory of Intelligent Information Processing and Emotional Computing in Jiangxi Province, Jiangxi Normal University, Nanchang 330022
3. School of Mathematics and Statistics, Xidian University, Xi'an 710071
4. School of Information Engineering, Jiangxi University of Water Resources and Electric Power, Nanchang 330099
5. School of Computer and Big Data Science, Jiujiang University, Jiujiang 332005
Corresponding author:
PENG Hu, Ph.D., professor. His research interests include evolutionary computation and its applications.

About Author:
ZHOU Xinyu, Ph.D., associate profe-ssor. His research interests include intelligent computation.
JIANG Jinfeng, Master. His research interests include constrained evolutionary optimization.
GAO Weifeng, Ph.D., professor. His research interests include intelligent computation and deep learning.
WANG Hui, Ph.D., professor. His research interests include intelligent computation.

Fund:National Natural Science Foundation of China(No.62366022,62276202,62166027,62266024), Natural Science Foundation of Jiangxi Province(No.20232BAB202048), Outstan- ding Youth Foundation of Natural Science Foundation of Jiangxi Province(No.20212ACB212004)
Abstract

Constrained differential evolution(CDE) algorithm is an effective way to solve constrained optimization problems. However, the existing research mainly focuses on constraint handling techniques, while the differential evolution algorithm itself is neglected, resulting in some problems, including unbalanced exploration and exploitation capabilities, and a low survival rate of offspring individuals of feasible solutions. To address these issues, a dynamic elite learning strategy is designed to improve the performance of the CDE algorithm. In this strategy, the individuals in the population are divided into ordinary feasible solutions, elite feasible solutions and infeasible solutions, and individualized mutation operators are adopted for each of these three types of individuals to balance the exploration and exploitation capabilities. Meanwhile, the elite feasible solutions are introduced to improve the classical mutation operators, thereby increasing the survival rate of offspring of feasible solutions. According to the characteristics of infeasible solutions, a fine-tuned feasibility rule is also designed as a constraint handling technique to better guide the population into the feasible region. Experiments on CEC2006, CEC2010 and CEC2017 test sets as well as three real-world engineering optimization problems demonstrate that the proposed algorithm achieves superior performance compared with six state-of-art constrained optimization evolutionary algorithms.

Key words: Constrained Optimization; Differential Evolution; Feasibility Rule; Feasible Solution; Infeasible Solution

在实际生产生活中, 约束优化问题(Constrained Optimization Problem, COP)十分常见, 如机械手移动路径规划问题[1]、三杆桁架设计问题[2]等, 这类问题的求解具有挑战性.

通常, COP可形式化表示为

$\begin{array}{ll} \min & f(\boldsymbol{x}), \boldsymbol{x}=\left(x_{1}, x_{2}, \cdots, x_{D}\right) \in S, L_{i} \leqslant x_{i} \leqslant U_{i}, \\ \text { s. t. } & g_{j}(\boldsymbol{x}) \leqslant 0, j=1, 2, \cdots, l, \\ & h_{j}(\boldsymbol{x})=0, j=l+1, l+2, \cdots, l+m, \end{array}$

其中, f(x) 表示目标函数, x=(x1, x2, …, xD)表示决策向量,

S= ∏i=1D[Li, Ui]

表示搜索空间, D表示优化问题的维度, Ui、Li表示xi的上限和下限, gj(x)表示不等式约束, hj(x)表示等式约束, l表示不等式约束个数, m-l表示等式约束个数.此外, 决策向量x也称为解x, 其在所有约束条件上的总违反程度如下所示:

G(x)= ∑j=1mGj(x),

其中,

Gj(x)= max(0, gj(x)), 1≤j≤lmax(0, hj(x)-δ), l+1≤j≤m

表示解x在第j个约束上的违反程度, δ 表示容忍参数, 值非常小, 一般设为0.000 1.如果解x满足G(x)=0, 则x为可行解; 如果G(x)不为0, 则x为不可行解.通常来说, 求解COP的目标就是找到最优可行解.

近年来, 在求解COP的相关算法中, 进化算法(Evolutionary Algorithm, EA)优势显著, 具有较强的鲁棒性和广泛的适用性.然而, 由于缺乏处理约束条件的能力, EA难以直接用于求解COP, 需结合约束处理技术(Constraint Handling Techniques, CHT)以形成可求解COP的约束优化进化算法(Constrained Optimization Evolutionary Algorithm, COEA), 即

COEA=EA+CHT.

因此, 对于COEA而言, 算法应包含两部分内容:一部分是通过EA搜索解空间生成新种群, 推动种群不断向最优可行解靠拢; 另一部分是采用CHT对比个体之间的优劣程度, 保留较好个体.需注意的是, 此处的“ 较好” 可能是指个体的目标函数值较好, 也可能是个体的约束违反程度较小, 不同的COEA做法不同.

当前, 已有很多不同类型的COEA被相继提出, 相关算法求解效果较优, 但值得注意的是, 这些算法的设计重点主要集中在CHT部分, 而在EA部分存在两方面的不足.1)对所有个体一视同仁, 无差别地选择变异算子, 忽视不同个体对变异算子的需求不同, 使算法的勘探和开采能力不平衡, 导致算法出现早熟或求解精度较低等问题.2)采用的变异算子往往是经典的变异算子, 未考虑个体生成后代在约束条件下的质量.例如:当可行解位于可行域的边界附近时, 通过经典变异算子生成的后代个体很可能是不可行的, 容易导致可行解的后代存活率较低.

基于上述考虑, 本文提出动态精英学习的约束差分进化算法(Constrained Differential Evolution Al-gorithm with Dynamic Elite Learning, DELDE).为EA部分设计动态精英学习策略, 将种群内的个体划分为普通可行解、精英可行解、不可行解, 再为这三部分个体采用不同类型的变异算子, 满足不同个体对于变异算子的个性化需求, 进一步平衡算法的勘探和开采能力.针对普通可行解, 设计融入精英可行解的变异算子, 发挥精英可行解的引导作用, 缓解可行解后代存活率较低的问题.对于精英可行解, 设计的变异算子也融入其它精英可行解, 强化精英可行解之间的信息交互.此外, 在CHT部分还设计微调的可行性规则, 同时考虑个体的约束违反程度和目标函数值, 在推动种群快速进入可行域的同时, 减少种群滞留在不可行域中的情况.在CEC2006、CEC2010、CEC2017测试集及3个实际工程优化问题上, 与6种知名的COEA进行对比(包含CEC2017约束优化竞赛的冠军算法), 结果表明本文算法的整体性能更优.

1 相关工作及存在问题
1.1 相关工作

当前, 从COEA采用的EA范例来看, 大部分相关工作均采用差分进化算法(Differential Evolution, DE), 主要原因是DE的搜索效率较高、结构简单, 因此这类算法也被称为约束DE (Constrained Diffe-rential Evolution, CDE).按DE中变异算子的特点可将约束DE大致分为单策略CDE和多策略CDE.

单策略CDE是指算法中只用到一种变异算子, 通常是一种经典的变异算子或改进的变异算子[3].Cui等[4]根据后代种群中成功更新的个体比例动态调整DE/rand/1的缩放因子和交叉概率.Gao等[5]提出DPDE(Dual-Population Differential Evolution), 设计两个种群, 分别优化目标函数和约束违反程度, 在双种群的基础上改进DE/rand/1, 从其中一个种群中随机选择 xr1t和 xr2t, 再从两个种群中随机选取 xr3t.此方式有力促进两个种群之间的信息交互.Li等[6]提出CO-JADE(Differential Evolution Algorithm Based on Adaptive Differential Evolution), 直接使用Zhang等[7]设计的DE/current-to-pbest算子, 同时还结合基于档案的自适应权衡模型以求解COP.Gong等[8]提出ARMOR(Adaptive Ranking Mutation Opera-tor), 先根据种群中可行解的比例对个体排序, 再将排名前列的个体用于生成后代个体, 提高算法的收敛能力.Hamza等[9]基于约束一致性的方法设计新的变异算子, 目的是在搜索过程中引导种群向可行域靠近.Yu等[10]改进DE/rand/1, 以三个随机选择的个体中的最优个体作为基向量, 提升种群的开采能力.

多策略CDE是指算法利用两种及以上的变异算子, 这些算子具备不同特性, 能进一步增强算法的搜索能力和种群的多样性.Wang等[11]提出FROFI(Feasibility Rule with the Incorporation of Objective Function Information), 以相同的概率使用DE/current-to-rand/1和DE/rand-to-best/1这两种变异算子, 并对缩放因子和交叉概率设置参数候选池, 以随机的方式从候选池中为这两个参数选取参数值.与FROFI不同的是, 在文献[12]中, DE/current-to-rand/1和DE/rand-to-best/1这两种变异算子的使用概率与迭代次数有关, DE/current-to-rand/1在迭代前期的使用概率较高, 而DE/rand-to-best/1在迭代后期的使用概率较高, 这种动态调整的方式能更好地实现勘探和开采之间的平衡.Li等[13]提出CCEF(Competitive and Cooperative Evolutionary Framework), 使用DE/current-to-rand/1和带有档案的DE/rand-to-pbest/1这两种变异算子, 并根据成功更新的个体数量动态调整两种变异算子的选择概率.Wang等[14]提出C2oDE(Constrained Composite Differential Evolu- tion), 在CoDE(Composite Differential Evolution)[15]的基础上结合两种不同的CHT以求解COP.在C2oDE中, 每个个体会先通过三种经典变异算子同时生成三个后代个体, 再采用可行性规则选择最好的后代个体, 最后使用ε 约束方法对比选择的后代个体与父代个体.

1.2 存在问题

近年来, 大部分COEA主要聚焦在CHT部分, 对EA部分关注较少.在单策略CDE相关工作中, 所有个体均采用经典的DE/rand/1或简单改进的DE/rand/1生成后代.在多策略CDE相关工作中, 尽管算法采用多种变异算子, 但对于种群或子种群中的所有个体而言, 使用变异算子的方式是相同的, 并且采用的变异算子仍为经典的变异算子.

虽然上述方式简单有效, 能为算法提供较强的搜索能力, 但不论是单策略CDE, 还是多策略CDE, 在EA部分还存在两点缺陷.

1)算法未考虑不同个体对变异算子的需求不同, 为种群或子种群中的所有个体无差别地选择变异算子, 导致算法的勘探和开采能力不平衡.

2)采用的经典变异算子容易导致可行域边界附近可行解的后代存活率过低, 即当可行解位于可行域边界附近时, 通过这些经典变异算子生成的后代往往是不可行的, 尽管有一些相关工作对经典变异算子进行简单改进, 但其目的并非是为了提高可行解后代的存活率.

针对缺陷1), 从个体的角度上看, 种群内的个体不仅可按其是否满足约束条件划分为不可行解和可行解, 对可行解还可按目标函数值进一步细分为普通可行解和精英可行解.这三部分个体具有不同特点, 对变异算子的需求也不同.不可行解对维持种群的多样性发挥重要作用, 需勘探能力较强的变异算子探索整个解空间.普通可行解的目标函数值相对较差, 仅需开采能力较强的变异算子快速提升自身质量.对精英可行解而言, 既需要勘探能力较强的变异算子以探索更多的可行域, 同时又需要开采能力较强的变异算子提升算法的收敛能力.因此, 若能针对性地为这三部分个体采用不同特性的变异算子, 可充分发挥不同变异算子的作用, 更好地平衡算法的勘探和开采能力.

针对缺陷2), 因经典变异算子对可行域边界附近的可行解容易生成不可行后代, 可在变异算子中利用精英可行解的信息, 引导后代在可行域中生成, 提高可行解后代的存活率.

为了更好地说明这一情况, 图1给出一个具体实例, 图中橙点是位于可行域边界附近的普通可行解xi, 红点为精英可行解xelite, 黑圈表示通过经典变异算子为xi生成的后代所处的可能范围.

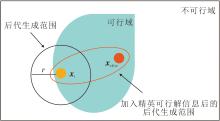图1 利用精英可行解xelite指导后代生成示意图Fig.1 Schematic diagram of offspring generation guided by elite feasible solution xelite

由图1可看出, xi后代所处的可能范围有近一半面积为不可行域, 因此该后代在很大程度上也可能是不可行解, 当与父代xi竞争时往往难以存活.然而, 若能在变异算子中利用xelite, 可在生成该后代的过程中把其拉向xelite, 即后代所处的可能范围会向xelite靠拢, 形成图中的红色椭圆范围, 从而提高后代的存活率.

2 动态精英学习的约束差分进化算法

本文提出动态精英学习的约束差分进化算法(DELDE), 核心包含两部分.

1)动态精英学习策略, 将种群中的个体划分为普通可行解、精英可行解、不可行解三部分, 并为每部分采用个性化变异算子, 平衡算法的勘探与开采能力.

2)微调的可行性规则, 同时考虑约束违反程度与目标函数值, 快速推动种群进入可行域.

2.1 动态精英学习策略

在动态精英学习策略中, 首先将种群内的个体按其是否满足约束条件划分为不可行解和可行解, 再将可行解按目标函数值进一步细分为普通可行解和精英可行解, 从而把种群内的个体划分为三部分, 之后为这三部分个体采用不同特性的变异算子, 满足不同个体对于变异算子的个性化需求.动态精英学习策略的示意图如图2所示.

图2 动态精英学习策略示意图Fig.2 Schematic diagram of dynamic elite learning strategy

下面详细介绍为这三部分个体采用的不同变异算子.

1)不可行解的变异算子.不可行解的主要任务是广泛探索整个解空间, 并维持种群的多样性.因此, 其变异算子的选择原则是优先保证较强的勘探能力, 为此采用变异算子DE/current-to-rand/1, 该算子表达式如下:

vit= xit+rand(0, 1)· (xr1t- xit)+F· (xr2t- xr3t).

其中, xit表示目标个体, rand(0, 1)表示[0, 1]内的随机数, xr1t, xr2t, xr3t表示种群中随机选择的互不相同的个体, F表示缩放因子.

该算子采用多个随机个体, 具有较强的全局探索能力, 但过度使用容易导致算法收敛速度减慢.为此, 不可行解还继续采用具有较强开采能力的变异算子DE/rand-to-best/1, 以期平衡勘探和开采能力.该算子表达式如下:

vit= xr1t+F· (xbestt- xr1t)+F· (xr2t- xr3t),

其中 xbestt表示种群中基于目标函数值的最好个体.这两种变异算子以均等概率选择使用[16, 17].

针对这两种变异算子, 为缩放因子F和交叉概率CR设置参数候选池:

F={0.6, 0.8, 1.0}, CR={0.1, 0.2, 1.0},

从中随机选取参数值.该方式在CDE的相关工作中也被广泛使用[11, 12].需注意的是, DE/rand-to-best/1采用二项式交叉算子, 而DE/current-to-rand/1具备旋转不变性, 无需交叉算子.

2)普通可行解的变异算子.普通可行解的目标函数值要差于精英可行解, 其主要任务是快速提升自身质量, 生成具有更好目标函数值的后代.其变异算子的选择原则是强化局部开采能力, 为此选用DE/current-to-best/1, 该算子表达式如下:

vit= xit+F· (xbestt- xit)+F· (xr1t- xr2t).

事实上, 为不可行解选用的DE/rand-to-best/1也具有一定的开采能力, 然而DE/current-to-best/1仅采用两个随机个体, 少于DE/rand-to-best/1的三个, 因此在一定程度上看, DE/current-to-best/1的开采能力更强, 更适合普通可行解.

此外, 当DE/current-to-best/1中的 xbestt为不可行解时, 普通可行解生成的后代很可能会被拉向不可行域, 导致后代的存活率较低.为此, 可将精英可行解融入DE/current-to-best/1, 将 xbestt替换为精英可行解 xelitet, 通过 xelitet指导普通可行解尽可能在可行域中生成后代, 提升后代的存活率.相应地, DE/ current-to-best/1被修改为DE/current-to-elite/1, 该算子表达式如下:

vit= xit+F· (xelitet- xit)+F· (xr1t- xr2t),

其中, xelitet表示随机选取的一个精英可行解, 并未固定为某一个精英可行解.该方式在一定程度上可提高种群的多样性, 避免过度使用同一精英可行解导致算法过早收敛.

针对DE/current-to-elite/1, 其缩放因子F和交叉概率CR的参数设置与不可行解保持相同, 此处不再赘述.

3)精英可行解的变异算子.精英可行解是当前种群内最好的一类解, 其变异算子的选择原则考虑如下两方面:既需勘探能力较强的变异算子以探索更多的可行域, 帮助种群跳出局部最优, 又需开采能力较强的变异算子加速收敛.因此, 为精英可行解采用DE/current-to-rand/1和DE/rand-to-best/1这两种变异算子, 使用方式和参数设置与不可行解相同.类似地, 当DE/rand-to-best/1中的 xbestt为不可行解时, 同样会导致精英可行解面临后代存活率较低的问题.为此, 可将其它精英可行解也融入DE/rand- to-best/1, 将 xbestt替换为精英可行解 xelitet以形成DE/rand-to-elite/1, 该算子表达式如下:

vit= xr1t+F· (xelitet- xr1t)+F· (xr2t- xr3t),

其中 xelitet表示随机选取的一个精英可行解.该方式既能提升精英可行解后代的存活率, 又可增强精英可行解之间的信息交互.

为普通可行解和精英可行解采用的变异算子均包含精英可行解 xelitet, 并且是以随机选择的方式使用的, 因此, 精英可行解的数量对于变异算子的性能具有重要影响.当精英可行解在所有可行解中比例过小时, 普通可行解的数量多于精英可行解会导致DE/current-to-elite/1被过度使用, 减少种群的多样性, 引起算法过早收敛, 相反, 当比例过大时, 精英可行解的数量会多于普通可行解, DE/current-to- rand/1有更多机会被频繁调用, 导致算法的开采能力不足, 收敛速度变慢.为此, 在动态精英学习策略中对精英可行解的比例采用动态调节方式, 具体精英可行解个数为:

$N e=\text { round }\left(\left(\frac{\text { MaxGen }-t}{\text { MaxGen }-t f}\right) N f\right) .$

其中:round(· )表示四舍五入取整函数, 确保Ne为整数; Nf表示可行解的数量, MaxGen表示算法的最大迭代次数, t表示当前迭代次数, tf表示种群中首次出现可行解时的迭代次数.

当种群中首次出现可行解时, tf与t相同, MaxGen-tf表示剩余的有效迭代次数, 此时所有可行解均为精英可行解.在后续的进化过程中, 随着迭代次数不断增加, 即t不断增大, 精英可行解的比例从1逐渐减至0, 但需注意的是, Ne的最小值被设为1, 以确保精英可行解的数量不少于1.从Ne的变化趋势来看, 在种群中出现可行解后, 较高的精英可行解比例能帮助种群找到更多的可行域, 以便向最优可行解靠拢; 而在迭代后期, 普通可行解的比例会升高, 可在精英可行解附近不断进行精细搜索, 以此找到最优可行解.

2.2 微调的可行性规则

可行性规则[18]是一种约束处理技术, 被广泛应用于COEA中[19, 20, 21].对于任意给定的两个个体x和y, 当满足如下条件中任意一条时, 称x优于y:

1)G(x)=0, G(y)=0, 并且f(x)< f(y),

2)G(x)> 0, G(y)> 0, 并且G(x)< G(y),

3)G(x)=0, G(y)> 0.

然而, 第2条“ 对于2个不可行解, 仅通过约束违反程度判断优劣” , 在优化问题的解空间存在欺骗性地形(即越靠近可行域, 约束违反程度反而越高)的情况下, 该条准则容易导致种群滞留在不可行域中.因此, 为了更全面地评估不可行解之间的优劣, 应综合考虑多方面信息, 而不仅仅局限于约束违反程度.

为此, 本文采用加权和的方式结合约束违反程度与目标函数值以构建适应度值, 使用适应度值作为判定不可行解之间优劣的标准, 具体不可行解 xit的适应度值表示如下:

F(xit)=ω G(xit)+(1-ω )f(xit),

其中, G(xit)、 f(xit)表示不可行解 xit的约束违反程度和目标函数值, ω ∈ [0, 1]表示权重.ω 的取值决定约束违反程度在适应度值中的比重大小:若取值过大, 同样容易导致种群滞留在不可行域中; 若取值过小, 目标函数值在适应度值中的比重较大, 会使算法过度优化目标函数, 而忽视解的可行性, 最终导致无法找到可行解.为此, 对于适应度函数F(· )中的权重ω 设计动态调节方式:

ω =0.5+ r·tMaxGen,

其中, r表示增长率, 用于控制ω 的变化速度.

从ω 的变化趋势上看, 在迭代前期通过考虑约束和目标函数两方面的信息对比两个不可行解, 可缓解种群滞留在不可行域中的情况.同时, 随着迭代次数增加, ω 会逐渐增大, 可持续推动种群向可行域靠拢.

除了上述动态调节方式以外, 为了进一步降低种群滞留在不可行域中的可能性, 本文还采用一种COEA中广泛使用的重启策略[14, 15, 16]:1)种群内所有个体均为不可行解; 2)所有个体约束违反程度的标准差小于1.0e-08.当这两个条件同时成立时, 说明种群很可能已滞留在不可行域中, 失去寻找最优可行解的能力, 此时将触发重启策略, 以随机初始化的方式重新生成种群, 继续求解约束优化问题.

2.3 算法伪代码

DELDE伪代码如算法1所示.

算法1 DELDE

输入 种群规模NP, 增长率r,

预设的最大目标函数评估次数MaxFEs,

参数候选池F={0.6, 0.8, 1.0},

CR={0.1, 0.2, 1.0}

输出 最优可行解

1.随机生成NP个个体以构成初始种群P, 评估P中所有个体的目标函数值和约束违反程度;

2.FEs=NP, t=1; /* t表示当前迭代次数, FEs表示消耗的评估次数* /

3.while FEs ≤ MaxFEs do

4. 统计种群内可行解的数量Nf;

5. if Nf> 0 then

6. 计算Ne, 将可行解划分为普通可行解和精英可行解;

7. end if

8. for i=1∶ NP do

9. 从参数候选池中为F和CR随机选取参数值;

10 if xit为不可行解then

11. 以均等概率选用DE/current-to-rand/1和DE/rand-to-best/1生成后代个体 vit;

12. else if xit为普通可行解then

13. 使用DE/current-to-elite/1生成后代个体 vit;

14. else if xit为精英可行解then

15. 以均等概率选用DE/current-to-rand/1和DE/rand-to-elite/1生成后代个体 vit;

16. end if

17. end for

18. 评估所有后代个体的目标函数值和约束违反程度;

19. FEs=FEs+NP;

20. for i=1∶ NP do

21. if xit与 vit均为不可行解then

22. 计算F(xit)和F(vit), 选择更优个体进入下一代种群;

23. else

24. 根据可行性规则对比 xit和 vit, 选择更优个体进入下一代种群;

25. end if

26. end for

27. 执行重启策略, t=t+1;

28.end while

与经典CDE相比, DELDE主要有如下4点不同.

1)第5~7行将种群内的可行解细分为普通可行解和精英可行解.

2)第10~16行为不可行解、普通可行解及精英可行解分别采用不同的变异算子.

3)第13行和第15行将精英可行解融入两种经典变异算子.

4)第21~25行对可行性规则进行微调, 当父代个体和子代个体均为不可行解时, 根据适应度值选择更优个体进入下一代种群.

3 实验及结果分析
3.1 实验设置

为了验证DELDE性能, 在CEC2006[22]、CEC-2010[23]、CEC2017[24]这3个广泛使用的测试集上进行大量实验.CEC2006测试集包含24个测试问题, 维度从2维至24维不等.CEC2010测试集包含18个测试问题, 维度为10维和30维.CEC2017测试集包含28个测试问题, 维度为50维和100维.这些测试问题均为最小化问题, 具有不同特性, 能综合评估算法性能, 如非线性、多模态性、搜索空间狭窄和旋转性等.

表1给出各测试集上目标函数的最大评估次数MaxFEs和种群规模NP的参数设置.对于所有测试问题, 等式约束的容忍参数δ 设为0.000 1.需说明的是, MaxFEs和δ 是按测试集的相应原文献进行设置.

表1 各测试集上具体参数设置 Table 1 Parameter settings on different datasets

实验环境包括Intel(R)Core(TM)i5-8300H CPU@2.30 GHz、16 GB DDR4 RAM、R2021a版本Matlab.

3.2 对比实验

3.2.1 对比算法

为了综合评估DELDE性能, 选取如下6种知名COEA进行对比.

1)FROFI[11].以均等概率选用两种变异算子, 并结合融入目标函数信息的可行性规则求解COP.

2)DeCODE[12].将COP转化为双目标优化问题, 再使用基于分解的多目标优化方法求解转化后的问题.

3)CCEF[13].采用基于竞争与合作的进化框架, 使用4种CHT技术和2种变异算子.

4)C2oDE[14].EA部分使用无约束算法CoDE, CHT部分结合可行性规则和ε 约束方法.

5)DeDP[16].CHT部分采用惩罚函数方式, 使用一个分解框架将COP转化为多个无约束优化子问题, 并为每个子问题分配一个惩罚系数, 平衡约束和目标函数.

6)LSHADE44[25].通过一种竞争机制使用两种变异算子和交叉算子, 该方法是CEC2017约束优化竞赛的冠军算法.

实验中所有对比算法的参数设置与原文献保持一致, 每种算法均在所有测试问题上独立运行25次, 记录实验结果的均值和标准差.

3.2.2 在CEC2006测试集上的实验

本节在CEC2006测试集上进行对比实验, 对比算法包括FROFI、C2oDE、DeCODE、DeDP、CCEF.因DeDP原文献中未涉及CEC2006测试集上的相关实验, 所以实验中将DeDP的种群规模设置与DELDE相同.

此外, CEC2006测试集提供每个测试问题的最优值, 若算法在一次运行中求得的实际最优值与该最优值之间的差值小于0.000 1, 可认定算法此次运行成功.

各算法的实验结果如表2所示, 表中符号* 表示算法在相应测试问题上每次都能运行成功.由于所有算法在测试问题g20、g22上均无法找到可行解, 因此实验中未记录这两个测试问题的结果.

表2 各算法在CEC2006测试集上的实验结果 Table 2 Experimental results of different algorithms on CEC2006 test set

由表2可看出, C2oDE、DeCODE和DELDE在20个测试问题上每次都能运行成功.相比之下, FROFI、DeDP和CCEF分别在19个、17个和16个测试问题上每次都能运行成功.特别地, 对于测试问题g02, 仅有DELDE每次都能运行成功, 主要原因是该测试问题具有多个局部最优区域, 在种群陷入局部最优区域之后, 融入精英可行解的变异算子能帮助种群跳出该区域.

对于测试问题g17, 所有算法均未做到每次都能运行成功, 可能原因是该测试问题的约束条件均为非线性等式约束, 并且目标函数也有非线性特征, 使得问题的解空间异常复杂.从整体上看, DELDE平均在1.6个问题上结果更优, 整体性能略优于对比算法.

3.2.3 在CEC2010测试集上的实验

本节进一步将DELDE在CEC2010测试集上进行实验, 对比算法包括FROFI、C2oDE、DeCODE、DeDP、CCEF.

为了在统计意义上对比算法之间性能是否存在显著性差异, 采用非参数的Wilcoxon秩和检验对比结果, 显著性水平设为0.05, 符号+、-和=分别表示DELDE在相应测试问题上显著优于、差于和相似于对比算法.

维度为10时各算法的实验结果如表3所示, 表中黑体数字表示最优值.由表可看出, DELDE在14个测试问题上取得最优值, 其次是DeCODE, 在10个测试问题上取得最优值.

表3 各算法在CEC2010测试集上维度为10时的实验结果 Table 3 Experimental results of different algorithms on CEC2010 test set at a dimensionality of 10

具体而言, DELDE分别在12个、6个、6个、7个和14个测试问题上优于FROFI、C2oDE、DeCODE、DeDP和CCEF, 而FROFI、C2oDE、DeCODE、DeDP和CCEF仅分别在2个、2个、3个、2个、1个测试问题上优于DELDE.

维度为30时各算法的实验结果如表4所示, 表中黑体数字表示最优值.由表可看出, DELDE在11个测试问题上取得最优值, 其次是C2oDE, 在7个测试问题上取得最优值.由此可见, 测试问题维度升高时, DELDE依然能在多数测试问题上取得最优值, 具有较好的鲁棒性.

表4 各算法在CEC2010测试集上维度为30时的实验结果 Table 4 Experimental results of different algorithms on CEC2010 test set at a dimensionality of 30

具体地, DELDE分别在11个、7个、6个、10个和10个测试问题上优于FROFI、C2oDE、De-CODE、DeDP和CCEF, 而FROFI、C2oDE、DeCODE、DeDP和CCEF分别在4个、4个、4个、2个、5个测试问题上优于DELDE.

在测试问题c01上, DELDE在10维和30维时均取得最优值, 主要原因是该测试问题的可行域占比较大, 种群能快速进入可行域, 融入精英可行解的变异算子为算法提供较强的收敛能力.

对于测试问题c03, 其可行域占比非常小, 但DELDE在10维和30维时仍能取得最优值, 这说明DELDE具有很强的寻找可行域的能力.

从表3和表4的Wilcoxon秩和检验结果上看, 相比对比算法, DELDE平均在9个测试问题上结果更优.

为了进一步分析实验结果, 还采用Friedman检验评估所有算法在测试集上的整体性能差异.检验结果如下:DELDE排名值为2.6528, 位居第一, CCEF排名值为3.1667, 排在第二位, C2oDE和DeCODE并列第三, FROFI排名第四, DeDP排名第五.综上所述, DELDE在CEC2010测试集上的性能优于对比算法.

3.2.4 在CEC2017测试集上的实验

本节在CEC2017测试集上进行对比实验, 对比算法包括LSHADE44、DeCODE、DeDP、CCEF.实验依旧采用Wilcoxon秩和检验对比结果, 显著性水平设为0.05.

由于所有算法在测试问题c17、c18、c19、c26、c27、c28上时无法找到可行解, 因此实验中未记录这6个测试问题的检验结果.

维度为50时各算法的实验结果如表5所示, 表中黑体数字表示最优值, ▽表示算法在相应问题上运行25次均无法找到可行解.由表可看出, DELDE分别在13个、18个、10个和12个测试问题上优于LSHADE44、DeCODE、DeDP和CCEF.相比之下, LSHADE44、DeCODE、DeDP和CCEF分别在7个、2个、6个和5个测试问题上优于DELDE.在测试问题c06上, LSHADE44在25次运行中均无法找到可行解, 可能原因是该测试问题的解空间存在欺骗性地形, 算法采用的可行性规则导致种群滞留在不可行域中.

表5 各算法在CEC2017测试集上维度为50时的实验结果 Table 5 Experimental results of different algorithms on CEC2017 test set at a dimensionality of 50

维度为100时各算法的实验结果如表6所示, 表中黑体数字表示最优值.由表可看出, LSHADE44和DELDE均在7个测试问题上取得最优值, 而DeCODE、DeDP和CCEF分别在1个、1个和6个测试问题上取得最优值.具体地, DELDE分别在13个、12个、12个和12个测试问题上优于LSHADE44、DeCODE、DeDP和CCEF, 而LSHADE44、DeCODE、DeDP和CCEF分别在9个、7个、5个和8个测试问题上优于DELDE.

表6 各算法在CEC2017测试集上维度为100时的实验结果 Table 6 Experimental results of different algorithms on CEC2017 test set at a dimensionality of 100

对于测试问题c03, DELDE能取得最优值, 而DeCODE和DeDP的结果略差于DELDE, 这说明DELDE在测试问题c03上的收敛精度优于De- CODE和DeDP.

对于测试问题c21、c23, 它们的目标函数和约束条件均有旋转性, 而DELDE在这两个测试问题上都能取得最优值, 说明DELDE在求解具有旋转特征问题时也有较优表现.

从表5和表6的Wilcoxon秩和检验结果上看, 相比对比算法, DELDE平均在13个测试问题上结果更优.

所有算法的Friedman检验结果如下:DELDE排名值为2.7159, 位于第一名; CCEF排名第二, DeCODE、DeDP、LSHADE44为后三名.综上所述, 在CEC2017测试集上, DELDE的性能优于对比算法.

3.3 实际工程优化问题实验

为了进一步验证DELDE性能, 求解如下3个实际工程优化问题:焊接梁设计问题[26]、拉伸/压缩弹簧设计问题[2]、三杆桁架设计问题[2].

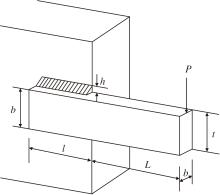
焊接梁常见于机械制造领域, 科学合理地设计焊接梁, 不仅可显著增强机械结构的稳定性, 还能有效降低制造成本.焊接梁设计问题的示意图如图3所示, 目的是在切应力τ 、弯曲应力σ 、弯曲载荷PC、末端偏差δ 的限制下, 找到一个最优向量X=(h, l, t, b), 使焊接梁的成本f(X)最小.该问题可形式化表示如下:

f(X)=1.10471h2l+0.04811tb(14+l),

g1(X)=τ (X)-13600,

g2(X)=σ (X)-30000,

g3(X)=h-b,

g4(X)=δ (X)-0.25,

g5(X)=6000-PC(X),

g6(X)=0.1047h2-0.04811tb(14+l)-5,

g7(X)=0.125-h,

其中,

$\begin{array}{l} \tau(\boldsymbol{X})=\sqrt{\left(\tau^{\prime}\right)^{2}+\frac{2 \tau^{\prime} \tau^{\prime \prime} l}{2 R}+\left(\tau^{\prime \prime}\right)^{2}}, \\ \tau^{\prime}=\frac{P}{\sqrt{2} h l}, \tau^{\prime \prime}=\frac{M R}{J}, \\ J=2\left\{\sqrt{2} h l\left[\frac{l^{2}}{12}+\left(\frac{h+t}{2}\right)^{2}\right]\right\}, \\ M=P\left(L+\frac{l}{2}\right), \\ R=\sqrt{\frac{l^{2}}{4}+\left(\frac{h+t}{2}\right)^{2}}, \\ P_{C}(\boldsymbol{X})=\frac{4.013 E \sqrt{\frac{t^{2} b^{6}}{36}}}{L^{2}}\left(1-\frac{t}{2 L} \sqrt{\frac{E}{4 G}}\right), \end{array}$

σ (X)= 6PLbt2, δ (X)= 4PL3Ebt3,

L=14, E=30× 106 psi, G=12× 106 psi,

0.1≤ h≤ 2, 0.1≤ b≤ 2,

0.1≤ l≤ 10, 0.1≤ t≤ 10.

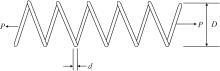
图3 焊接梁设计问题示意图Fig.3 Schematic diagram of welded beam design problem

弹簧是各类机械设备中的一种常见部件[2], 其设计对于设备的整体性能具有重要影响.拉伸/压缩弹簧设计问题的示意图如图4所示, 目的是在最小挠度g1、剪应力g2、冲击频率g3、外径g4的限制下, 找到一个最优向量X=(d, D, P), 使弹簧的重量f(X)最小.该问题可形式化表示如下:

$\begin{array}{l} f(\boldsymbol{X})=(P+2) D d^{2} \\ g_{1}(\boldsymbol{X})=1-\frac{D^{3} P}{71785 d^{4}} \\ g_{2}(\boldsymbol{X})=\frac{4 D^{2}-d D}{12566\left(D d^{3}-d^{4}\right)}+\frac{1}{5108 d^{2}}-1 \\ g_{3}(\boldsymbol{X})=1-\frac{140.45 d}{D^{2} P} \\ g_{4}(\boldsymbol{X})=\frac{d+D}{1.5}-1 \end{array}$

其中,

0.05≤ d≤ 2, 0.25≤ D≤ 1.3, 2≤ P≤ 15.

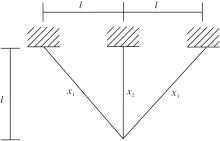
图4 拉伸/压缩弹簧设计问题示意图Fig.4 Schematic diagram of tension/compression spring design problem

三杆桁架是机械设备中常见的一种承重构件[2], 其设计在提高构件性能和降低制造成本等方面具有重要意义.三杆桁架设计问题的示意图如图5所示, 目的是在3种应力g1、g2、g3的限制下找到一个最优向量X=(x1, x2), 使桁架的体积f(X)最小.该问题的表达式如下:

$\begin{array}{l} f(\boldsymbol{X})=\left(2 \sqrt{2} x_{1}+x_{2}\right) l, \\ g_{1}(\boldsymbol{X})=\left(\frac{\sqrt{2} x_{1}+x_{2}}{\sqrt{2} x_{1}^{2}+2 x_{1} x_{2}}\right) P-\sigma, \\ g_{2}(\boldsymbol{X})=\left(\frac{x_{2}}{\sqrt{2} x_{1}^{2}+2 x_{1} x_{2}}\right) P-\sigma, \\ g_{3}(\boldsymbol{X})=\left(\frac{1}{\sqrt{2} x_{2}+x_{1}}\right) P-\sigma, \end{array}$

图5 三杆桁架设计问题示意图Fig.5 Schematic diagram of the three-bar truss design problem

其中,

0≤ x1≤ 1, 0≤ x2≤ 1,

l=100 cm, P=2 kN/cm2, σ =2 kN/cm2.

焊接梁设计问题、拉伸/压缩弹簧设计问题、三杆桁架设计问题的最大目标函数评估次数分别为1.5e+04、1.5e+04、6.0e+03.对比算法包括FROFI、C2oDE、DeCODE、DeDP、CCEF.除了种群规模以外, 对比算法的所有参数设置与原文献保持相同.对于种群规模, 因大部分对比算法的原文献未涉及上述3个实际工程优化问题的求解, 所以实验中将种群规模设为原文献中CEC2010测试集上维度为10时的大小.每种算法在所有问题上独立运行25次, 记录实验结果的均值和标准差.

各算法在3个实际工程优化问题上的实验结果如表7所示, 表中黑体数字表示最优值.由表可见, DELDE在全部问题上均取得最优值, 表明DELDE的性能最优.因此, 在这3个实际工程优化问题上, 相比FROFI、C2oDE、DeCODE、DeDP和CCEF, DEL-DE具有更优秀、更稳定的性能表现.

表7 各算法在3个实际工程优化问题上的实验结果 Table 7 Experimental results of different algorithms on three real-world engineering optimization problems
3.4 有效性验证

3.4.1 动态精英学习策略

动态精英学习策略包含3部分内容:1)将种群中的所有个体划分为不可行解、普通可行解、精英可行解, 并为这3类个体采用不同的变异算子, 满足不同个体对于变异算子的个性化需求; 2)采用精英可行解改进经典的变异算子, 提高可行解后代的存活率; 3)对于精英可行解的比例采用动态调节方式, 更好地平衡算法的探勘和开采能力.

为了验证动态精英学习策略的有效性, 设计3组对比实验:1)不区分种群中的个体, 为所有个体无差别地选择变异算子, 验证不同个体采用不同变异算子的有效性; 2)对比经典变异算子和采用精英可行解改进的变异算子, 验证改进变异算子的有效性; 3)将精英可行解的比例设为固定值, 验证动态调节方式的有效性.

所有实验均在CEC2010测试集上进行, 每种算法在所有测试问题上独立运行25次, 记录实验结果的均值.采用Wilcoxon秩和检验对比结果, 显著性水平设为0.05.

为了验证不同变异算子的有效性, 在DELDE基础上设计如下3种对比算法.

1)DELDE-ctr.所有个体仅使用DE/current-to-rand/1.

2)DELDE-rtb.所有个体仅使用DE/rand-to-best/1.

3)DELDE-cr.所有个体以均等概率选用DE/current-to-rand/1和DE/rand-to-best/1.

上述3种对比算法均为所有个体无差别地选择变异算子, 其余方面与DELDE保持相同, 因此可验证为不同个体采用不同变异算子的有效性.

所有算法的Wilcoxon秩和检验结果如表8所示.由表可看出DELDE的性能最优.具体而言, 相比单策略的DELDE-ctr和DELDE-rtb, DELDE分别在23个和21个测试问题上显著更优, 而仅分别在1个和4个测试问题上差于DELDE-ctr和DELDE-rtb.相比多策略的DELDE-cr, DELDE也具有较大优势, 在14个测试问题上显著更优, 而仅在1个测试问题上差于DELDE-cr.综上所述, 为不同个体采用不同变异算子要比为所有个体无差别地选择变异算子更有效.

表8 不同变异算子的Wilcoxon秩和检验结果 Table 8 Wilcoxon rank-sum test results of different mutation operators

为了验证改进变异算子的有效性, 在DELDE的基础上设计如下3种对比算法.

1)DELDE-np.所有个体采用经典变异算子.

2)DELDE-ap.所有个体采用改进的变异算子.

3)DELDE-ex.可行解采用经典变异算子, 不可行解继续采用改进的变异算子.

在上述3种对比算法中, 所有个体或部分个体采用经典变异算子或改进的变异算子, 其余方面与DELDE保持相同, 因此可验证采用精英可行解能提

升变异算子的有效性.所有算法的Wilcoxon秩和检验结果如表9所示, 由表可看出DELDE的性能最优.具体而言, DELDE在13个测试问题上优于DELDE-np, 而仅在1个测试问题上差于DELDE-np.相比DELDE-ap, DELDE在17个测试问题上显著更优, 未在任一测试问题上差于DELDE-ap.相比DELDE-ex, DELDE在17个测试问题上显著更优, 而仅在1个测试问题上差于DELDE-ex.综上所述, 采用精英可行解改进的变异算子优于经典变异算子.

表9 经典变异算子和改进变异算子的Wilcoxon秩和检验结果 Table 9 Wilcoxon rank-sum test results of classical mutation operators and improved mutation operators

为了验证精英可行解比例的有效性, 在DELDE的基础上, 固定精英可行解比例Er=0, 0.25, 0.50, 0.75, 1.00.需注意的是, 当Er=0时, 精英可行解的数量固定为1.

Er不同时的Wilcoxon秩和检验结果如表10所示, 由表可看出, DELDE的动态调节方式性能最优.具体而言, DELDE分别在16个、10个、11个、9个和10个测试问题上优于Er=0、Er=0.25、Er=0.50、Er=0.75和Er=1.00, 而Er=0和Er=0.75分别在2个和1个测试问题上优于DELDE.Er=0.25、Er=0.50和Er=1.00无法在任一测试问题上优于DELDE.

表10 不同精英可行解比例的Wilcoxon秩和检验结果 Table 10 Wilcoxon rank-sum test results of different elite feasible solution ratios

当精英可行解的比例较小时, 会导致大量的普通可行解过度使用DE/current-elite/1, 从而减少种群的多样性; 当精英可行解的比例较大时, DE/current-to-rand/1有更多机会被频繁调用, 导致算法的开采能力不足.综上所述, 动态调节的精英可行解比例优于固定比例.

3.4.2 微调的可行性规则

微调的可行性规则包含3部分内容:1)在经典可行性规则的基础上, 针对不可行解构建一种同时考虑约束违反程度和目标函数值的适应度函数, 使不可行解之间的对比不再仅由约束违反程度决定, 还会受到个体目标函数值的影响; 2)在适应度函数中, 对约束违反程度的权重ω 设计动态调节方式, 帮助种群更快进入可行域; 3)为了控制权重ω 的增长速度, 引入增长率r, r对算法性能具有重要影响.

为了验证微调的可行性规则的有效性, 相应设计3组对比实验:1)对比经典可行性规则, 验证微调的可行性规则的有效性; 2)将权重ω 设为固定值, 验证动态调节方式的有效性; 3)对增长率r进行敏感性分析, 确定最优值.

所有实验均在CEC2010测试集上进行, 每种算法在所有测试问题上独立运行25次, 记录实验结果的均值.采用Wilcoxon秩和检验对比结果, 显著性水平设为0.05.

为了验证微调的可行性规则的有效性, 在DELDE基础上设计如下两种对比算法.

1)DELDE-fit.CHT部分中所有个体仅采用适应度函数.

2)DELDE-fr.CHT部分中所有个体仅采用经典的可行性规则.

在DELDE的CHT部分, 适应度函数仅用于不可行解.与之不同的是, DELDE-fit的CHT部分中所有个体都可采用适应度函数.DELDE-fr的CHT部分中所有个体都采用经典的可行性规则.

各算法的Wilcoxon秩和检验结果如表11所示.由表可看出DELDE的性能最优.具体而言, DELDE共在29个测试问题上优于DELDE-fit, 而仅在1个测试问题上差于DELDE-fit.DELDE共在25个测试问题上显著优于DELDE-fr, 未在任一测试问题上差于DELDE-fr.综上所述, 微调的可行性规则优于经典可行性规则.

表11 不同可行性规则的Wilcoxon秩和检验结果 Table 11 Wilcoxon rank-sum test results of different feasibility rules

为了验证动态调节权重ω 的有效性, 在DELDE基础上, 固定ω =0, 0.25, 0.50, 0.75, 1.00, 不同取值时的Wilcoxon秩和检验结果如表12所示.由表可看出, DELDE的动态调节方式性能最优.

表12 不同ω 的Wilcoxon秩和检验结果 Table 12 Wilcoxon rank-sum test results with different ω

具体地, DELDE分别在22个、14个、12个、15个和25个测试问题上优于ω =0、ω =0.25、ω =0.50、ω =0.75和ω =1.00, 而ω =0、ω =0.25、ω =0.50仅分别在3个、6个和5个测试问题上优于DELDE, ω =0.75和ω =1.00无法在任一测试问题上优于DELDE.当权重ω 较小时, 算法过度优化目标函数, 忽视解的可行性, 最终导致无法找到可行解; 当ω 较大时, 在优化问题的解空间存在欺骗性地形, 容易导致种群滞留在不可行域中.因此, 动态调节的权重ω 优于固定权重ω .

增长率r控制权重ω 的增长速度, 对算法性能的影响具有重要作用.当增长率r较小时, 权重ω 增长较慢, 容易使算法过度优化目标函数, 最终导致无法找到可行解; 当r较大时, 快速增长的ω 会使算法过度优化约束条件, 容易导致种群滞留在不可行域中.

为了确定r的最优取值, 定义r=1.00, 1.25, 1.50, 1.75, 2.00, 相应的Wilcoxon秩和检验结果如表13所示.由表可看出, r=1.50时值最优.具体而言, r=1.50分别在10个、8个、12个和9个测试问题上优于r=1.00、r=1.25、r=1.75和r=2.00, 而r=1.00、r=1.25、r=1.75和r=2.00仅分别在2个、2个、1个和1个测试问题上优于r=1.50.因此建议r=1.50.

表13 不同r的Wilcoxon秩和检验结果 Table 13 Wilcoxon rank-sum test results with different r
4 结束语

对于COEA而言, 算法包含CHT和EA两部分, 这两部分对算法性能均有重要影响.然而, 现有COEA主要聚焦在CHT部分, 对EA部分关注较少, 导致算法面临两方面的不足.1)为所有个体无差别地选择变异算子, 容易使算法的勘探和开采能力不平衡; 2)采用的变异算子通常是经典的变异算子, 容易导致算法出现可行解后代存活率较低的问题.为此, 本文提出动态精英学习的约束差分进化算法(DELDE).设计动态精英学习策略, 将种群内的个体划分为普通可行解、精英可行解、不可行解, 并为这三部分个体采用不同类型的变异算子.采用精英可行解改进经典变异算子, 缓解可行解后代存活率较低的问题.对可行性规则进行微调, 针对不可行解构建一种同时考虑约束违反程度和目标函数值的适应度函数, 使用适应度值可更全面评估不可行解之间的优劣.

在CEC2006、CEC2010、CEC2017测试集及3个实际工程优化问题上进行大量实验, 得到如下结论:1)不论在测试集还是在实际工程优化问题上, DELDE性能都有很强的竞争力.2)为不同个体选用不同的变异算子要比为所有个体无差别地选择变异算子更有效.3)采用精英可行解改进的变异算子要比经典变异算子更有效.4)微调的可行性规则优于经典的可行性规则.5)对于精英可行解的比例和适应度函数中的权重ω 而言, 动态调节方式要优于固定值方式.

今后将尝试结合强化学习, 为个体选择不同变异算子, 同时还可尝试把DELDE用于求解更多的实际工程优化问题, 如类人机器人的步态优化问题、化工领域中连续流制造的调度优化问题等.

本文责任编委 何 清

Recommended by Associate Editor HE Qing

参考文献
[1] MA Y H, SHEN B, PAN A Q. Constrained Evolutionary Optimization Based on Dynamic Knowledge Transfer. Expert Systems with Applications, 2024, 240. DOI: 10.1016/j.eswa.2023.122450. [本文引用:1]
[2] LIU H, CAI Z X, WANG Y. Hybridizing Particle Swarm Optimization with Differential Evolution for Constrained Numerical and Engi-neering Optimization. Applied Soft Computing, 2010, 10(2): 629-640. [本文引用:5]
[3] QIAO K J, LIANG J, YU K J, et al. Self-Adaptive Resources Allocation-Based Differential Evolution for Constrained Evolutionary Optimization. Knowledge-Based Systems, 2022, 235. DOI: 10.1016/j.knosys.2021.107653. [本文引用:1]
[4] CUI C G, YANG X F, GAO T Y. A Self-Adaptive Interior Penalty Based Differential Evolution Algorithm for Constrained Optimization// Proc of the 5th International Conference on Advances in Swarm Intelligence. Berlin, Germany: Springer, 2014: 309-318. [本文引用:1]
[5] GAO W F, YEN G G, LIU S Y. A Dual-Population Differential Evolution with Coevolution for Constrained Optimization. IEEE Transactions on Cybernetics, 2015, 45(5): 1108-1121. [本文引用:1]
[6] LI K S, ZUO L, LI W, et al. A Novel Differential Evolution Algorithm Based on JADE for Constrained Optimization// Proc of the 7th International Symposium on Computational Intelligence and Intelligent Systems. Berlin, Germany: Springer, 2016: 84-94. [本文引用:1]
[7] ZHANG J Q, SANDERSON A C. JADE: Adaptive Differential Evolution with Optional External Archive. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945-958. [本文引用:1]
[8] GONG W Y, CAI Z H, LIANG D W. Adaptive Ranking Mutation Operator Based Differential Evolution for Constrained Optimization. IEEE Transactions on Cybernetics, 2015, 45(4): 716-727. [本文引用:1]
[9] HAMZA N M, ESSAM D L, SARKER R A. Constraint Consensus Mutation-Based Differential Evolution for Constrained Optimization. IEEE Transactions on Evolutionary Computation, 2016, 20(3): 447-459. [本文引用:1]
[10] YU X B, LI C L, ZHOU J F. A Constrained Differential Evolution Algorithm to Solve UAV Path Planning in Disaster Scenarios. Knowledge-Based Systems, 2020, 204. DOI: 10.1016/j.knosys.2020.106209. [本文引用:1]
[11] WANG Y, WANG B C, LI H X, et al. Incorporating Objective Function Information into the Feasibility Rule for Constrained Evolutionary Optimization. IEEE Transactions on Cybernetics, 2016, 46(12): 2938-2952. [本文引用:3]
[12] WANG B C, LI H X, ZHANG Q F, et al. Decomposition-Based Multiobjective Optimization for Constrained Evolutionary Optimization. IEEE Transactions on Systems, Man, and Cybernetics(Systems), 2021, 51(1): 574-587. [本文引用:3]
[13] LI Y C, GONG W Y, HU Z Z, et al. A Competitive and Cooperative Evolutionary Framework for Ensemble of Constraint Hand ling Techniques. IEEE Transactions on Systems, Man, and Cybernetics(Systems), 2024, 54(4): 2440-2451. [本文引用:2]
[14] WANG B C, LI H X, LI J P, et al. Composite Differential Evolution for Constrained Evolutionary Optimization. IEEE Transactions on Systems, Man, and Cybernetics(Systems), 2019, 49(7): 1482-1495. [本文引用:3]
[15] WANG Y, CAI Z X, ZHANG Q F. Differential Evolution with Composite Trial Vector Generation Strategies and Control Parame-ters. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 55-66. [本文引用:2]
[16] DANG Q L. Multiple Dynamic Penalties Based on Decomposition for Constrained Optimization. Expert Systems with Applications, 2022, 206. DOI: 10.1016/j.eswa.2022.117820. [本文引用:3]
[17] YUAN Y F, GAO W F, HUANG L L, et al. A Two-Phase Constraint-Hand ling Technique for Constrained Optimization. IEEE Transactions on Systems, Man, and Cybernetics(Systems), 2023, 53(10): 6194-6203. [本文引用:1]
[18] HUANG H, XU Y T, XIANG Y, et al. Correlation-Based Dyna-mic Allocation Scheme of Fitness Evaluations for Constrained Evolutionary Optimization. IEEE Transactions on Evolutionary Computation, 2024, 28(5): 1250-1264. [本文引用:1]
[19] LI J Q, LI G H, WANG Z K, et al. Differential Evolution with an Adaptive Penalty Coefficient Mechanism and a Search History Exploitation Mechanism. Expert Systems with Applications, 2023, 230. DOI: 10.1016/j.eswa.2023.120530. [本文引用:1]
[20] HU Z Z, GONG W Y, PEDRYCZ W, et al. Deep Reinforcement Learning Assisted Co-evolutionary Differential Evolution for Con-strained Optimization. Swarm and Evolutionary Computation, 2023, 83. DOI: 10.1016/j.swevo.2023.101387. [本文引用:1]
[21] WANG B C, FENG Y, LI H X. Individual-Dependent Feasibility Rule for Constrained Differential Evolution. Information Sciences, 2020, 506: 174-195 [本文引用:1]
[22] LIANG J, RUNARSSON T P, MEZURA-MONTES E, et al. Pro-blem Definitions and Evaluation Criteria for the CEC 2006 Special Session on Constrained Real-Parameter Optimization. Technical Report. Singapore, Singapore: Nanyang Technological University, 2006. [本文引用:1]
[23] MALLIPEDDI R, SUGANTHAN P N. Problem Definitions and Eva-luation Criteria for the CEC 2010 Competition on Constrained Real-Parameter Optimization. Technical Report. Singapore, CEC 2010 Competition on Constrained Real-Parameter Optimization. Technical Report. Singapore, Singapore: Nanyang Technological University, 2010. [本文引用:1]
[24] WU G H, MALLIPEDDI R, SUGANTHAN P N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization. Technical Report. Changsha, China: National University of Defense Technology, 2017. [本文引用:1]
[25] POLAKOVA R. L-SHADE with Competing Strategies Applied to Con-strained Optimization// Proc of the IEEE Congress on Evolutionary Computation. Washington, USA: IEEE, 2017: 1683-1689 [本文引用:1]
[26] HUANG F Z, WANG L, HE Q. An Effective Co-evolutionary Di-fferential Evolution for Constrained Optimization. Applied Mathematics and Computation, 2007, 186(1): 340-356 [本文引用:1]