假设所有设备的通信带宽与计算能力相对稳定.为了确保问题建模的严谨性, 定义如下概念和符号.

1)模型结构O={1, 2, …, o}, 表示DNN中所有算子的集合, i∈ O表示模型中第i层算子.

2)设备集合D={1, 2, …, d}, 表示所有可用设备的集合, j∈ D表示设备集合中的第j个设备.

3)设备属性(f, r)_j, 表示设备j的计算存储和通信能力, f_j表示第j个设备的计算能力, r_j表示设备的存储空间(如4 GB的LPDDR4X内存), 此外, 使用b表示设备的通信带宽.

4)算子配置 (cin, cout, wk, hk, s, p)i, 表示算子i的参数配置.对于卷积算子, cini表示输入通道数, couti表示输出通道数, wik表示卷积核宽度, hik表示卷积核高度, s表示滑动窗口步长, p表示特征图填充大小.由于全连接算子可等效为输入特征图尺寸为1× 1× cⁱⁿ、输出特征图尺寸为1× 1× c^out、卷积核大小为1的一种特殊卷积算子^[21], 因此, 可分别使用w^k、h^k表示全连接矩阵的输入维度和输出维度.

5)划分维度η _i= (ηic, ηoc)i, 其中, η _ic∈ {0, 1}, η _oc∈ {0, 1}, 表示算子i的划分维度.η _ic=1表示选择算子i的输入通道作为划分维度, η _oc=1表示选择算子i的输出通道作为划分维度, η _ic=0且η _oc=0表示不划分该算子.

6)(cini, j, couti, j), 表示将算子i沿通道维度划分后分配给设备j的通道数量, cini, j表示该部分输入通道数, couti, j表示该部分输出通道数, ω _{i, j}表示该部分算子权重的内存占用, a_{i, j}表示该部分输出激活值占用的内存大小.

基于模型结构和算子的配置信息, 可计算DNN中执行各算子所需的计算量.在执行DNN推理时, 部署于设备j上第i层算子的理论计算量如下所示:

c_{i, j}= cini, jcouti, jwikhikwoutihouti,

其中, cini, j、 couti, j表示部署在设备j上第i层卷积算子的输入通道数和输出通道数, wik、 hik表示第i层卷积算子的卷积核宽度和高度, wouti、 houti表示第i层卷积算子输出特征图的高度和宽度.

可根据算子配置的信息计算得到卷积算子输出特征图的宽度 wouti和高度 houti, 即

wouti= wini-wik+2psi+1, houti= hiin-hik+2psi+1,

其中, wini、 hini表示第i层算子输入特征图的高度和宽度, p表示填充大小, s_i表示步长大小.

由于全连接算子可等效为卷积核大小为1、输入特征图尺寸为1× 1× cⁱⁿ、输出特征图尺寸为1× 1× c^out的卷积算子, 因此, 其执行推理时所需计算量为:

c_{i, j}= cini, jcouti, j,

其中, cini, j、 couti, j表示全连接算子权重矩阵的输入维度和输出维度.

算子划分会导致设备之间产生通信开销, 并且该通信开销取决于算子的划分维度.算子划分引起的通信开销可归纳为如下三部分:

g_{i, j}=e+g cini, j+g couti, j,

其中, e表示设备间建立通信连接所需时间, g cini, j、g ci, jout表示沿输出通道维度和输入通道维度划分引入的通信开销.

对于卷积算子i, 如果相邻算子之间存在激活函数(如ReLU), 则沿输入通道维度划分所得的各部分输出必须在传递给后级算子之前进行拼接.因此, 对于算子i, 各设备计算生成的输出激活必须广播到其它设备, 该过程引起的通信量g cini, j= couti, jwouti, jhouti, j.

当设备j上算子i的输出通道数与其相邻下一级算子i+1的输入通道数相等, 即 couti, j= cini+1, j时, 无需进行输出激活的拼接操作, 因此不会产生额外的通信开销, 此时g couti, j=0.

对于全连接算子, 因其可视为一种特殊的卷积算子, 故其沿输入维度和输出维度划分引起的通信开销g cini, j=e+ couti, j.

在执行协同推理时, 如果DNN在推理时的峰值内存占用超过设备自身的存储能力, 会因为内存溢出(Out of Memory, OOM)而导致推理过程无法继续进行.因此, 定义约束条件如下:

s.t. ∑i∈Oω _{i, j}+max a_{i, j}≤ r_j, j∈ D.(1)

约束(1)表示部署在每个设备上的算子权重的内存占用与其最大输出激活的内存占用之和应小于该设备的可用存储空间.

在此基础上, 对算子的划分维度及算子划分前后的通道数量进行如下约束:

s.t. ∑n∈{0, 1}η _i(n)∈ {0, 1}, ∀ i∈ O.(2)

约束(2)表示模型中每个算子只能在输入通道和输出通道中选择一个维度进行划分.

划分后沿输入通道维度和输出通道维度拼接的各部分通道数之和应等于对应维度被划分前的通道数, 具体约束如下:

$\begin{array}{ll} \text { s. t. } & \sum_{j \in D} \eta_{i}(0) c_{i, j}^{\text {in }}=\eta_{i}(0) c_{i}^{\text {in }}, \\ & i \in O, c_{i, j}^{\text {in }} \geqslant 0, c_{i, j}^{\text {in }} \in \mathbf{Z} ; \end{array}$ (3)

$\begin{array}{ll} \text { s. t. } & \sum_{j \in D} \eta_{i}(1) c_{i, j}^{\text {out }}=\eta_{i}(1) c_{i}^{\text {out }} \\ & i \in O, c_{i, j}^{\text {out }} \geqslant 0, c_{i, j}^{\text {out }} \in \mathbf{Z} . \end{array}$ (4)

基于上述分析, 可得目标函数:

P1: min ∑ηi, i∈Omaxj∈D(Ti, jc+ Ti, jg),

函数约束条件如式(1)~式(4)所示.

模型的推理时间包括计算延迟和通信延迟. Ti, jc、 Ti, jg表示第i层算子在第 j个设备上的计算延迟和通信延迟, 具体公式如下:

$\begin{array}{l} T_{i, j}^{c}=\frac{c_{i, j}}{f_{j}}, i \in O, j \in D, \\ T_{i, j}^{g}=\frac{g_{i, j}}{b}, i \in O, j \in D, \end{array} $

其中, c_{i, j}表示计算量, g_{i, j}表示通信量, 这取决于采用的算子划分方式, f_j和b则由设备的计算能力和通信带宽等属性决定.

将基于IOP策略的协同推理描述为一个整数规划问题P1, 其目标在于寻求一种最小化协同推理时间的模型划分方式, 主要分为两步.

1)将模型划分为Γ ={γ ₁, γ ₂, …, γ _k}, 其中, γ _i表示一个模型分段, 可以是单个算子, 也可以是一对算子的组合, 即前后级通道数匹配的算子对.

2)对于每个算子对, 采用IOP策略, 通过匹配前后级算子通道数量, 避免输出激活的拼接过程, 减少设备间的通信开销.将两个算子作为构成算子对的最小组合, 是因为考虑到多个算子组合的方案会增加计算复杂度, 该约定是为平衡算法性能和推理延迟所做的一种折衷.

为了确定模型中采用IOP策略进行划分的算子, 设计算子配对算法, 示意图如图1所示.由图可见, 从CNN中的第1个算子开始, 逐算子搜索符合IOP条件的算子对.具体而言, 对于算子i及其后级算子i+1, 分别计算IOP策略和OCP策略下的推理延迟时间.若IOP策略下的推理延迟时间更短, 则将这两个算子配对, 即IOP策略下算子i和算子i+1构成交错式划分, 否则对算子i使用OCP策略.由于算子配对算法针对模型中的卷积算子和全连接算子, 因此, 为了突出重点, 在图1中省略模型中的ReLU和Softmax等激活函数.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 算子配对示意图Fig.1 Schematic diagram of operator pairing

算子配对算法具体步骤如下所示.

算法1 算子对配对算法

输入 算子集合O={1, 2, …, o},

设备集合D={1, 2, …, d},

算子配置 (cin, cout, wk, hk, s, p)i,

划分维度η _i, 设备属性(f, r)_j, b

输出 模型划分方案Γ ={γ ₁, γ ₂, …, γ _k}

初始化变量k=1, i=1 //初始化索引

for i in range(1, N): //遍历模型中的算子

γ _k=(i, i+1) //构造候选算子对

T_ocp=Evaluate_ocp(γ _k) //评估OCP策略下γ _k的推理延迟时间

T_iop=Evaluate_iop(γ _k) //评估IOP策略下γ _k的推理延迟时间

if T_iop< T_ocp: //如果IOP策略下γ _k的推理延迟时间更短

Γ ← γ _k //配对成功

k+1, i+2 //更新索引

else:

γ _k=(i) //单个算子作为分段

Γ ← γ _k //加入模型划分方案

i+1 // 更新索引

return Γ //返回模型划分方案

为了进一步评估算子配对算法的计算效率, 对其复杂度进行理论分析.设模型中共有N个算子, 则算法的时间复杂度和空间复杂度如下所述.

算法主体为一个从前向后遍历算子集合的循环结构.每轮迭代尝试构建当前算子与其后级算子的候选配对, 并在OCP策略与IOP策略下分别评估对应的推理延迟时间.评估函数Evaluate(γ _k)可基于算法输入的算子配置和设备属性参数, 在常数时间内完成计算.因此, 每轮迭代的时间复杂度为O(1).由于在匹配成功时索引i会递增两位, 否则递增一位, 因此, 整个循环最多执行N-1次.故算法的时间复杂度为O(N)× O(1)=O(N).

算法需存储生成的算子对集合Γ ={γ ₁, γ ₂, …, γ _k}, 该集合中的算子对数量最多不超过模型中全部算子数量的一半, 即N/2.算法中使用的索引变量及中间结果T_ocp和T_iop均为常量空间开销.因此, 算法的空间复杂度为O(N).

综上所述, 算子配对算法具有线性时间和空间复杂度, 适用于搜索大规模CNN的IOP部署方案.

本文实验平台包括i9-10980XE处理器、4张NVIDIA RTX 3090、1张NVIDIA RTX 4090、1张NVIDIA RTX 2080 Ti、1张NVIDIA GTX 1080 Ti、国产化设备寒武纪4芯MLU 220.运用torch.cuda.memory_allocated等函数限定设备可用的内存容量.同时, 引入冗余通信数据的方式调整设备间的传输带宽.

使用图像分类网络LeNet、AlexNet、VGG11、VGG13、VGG16、VGG19、ResNet-18、MobileNetv1和经典的目标检测网络YOLO-Fastest, 评估IOP策略下的推理延迟时间、异构设备环境的普适性、能耗及链路波动环境下的鲁棒性^{[32, 33]}.

输入模型的数据来自MNIST^[34]、CIFAR-10^[35]、ImageNet^[36]、CelebA^[37]、ISIC2018^[38]、Food-101^[39]、COCO^[40]、Oxford-IIIT^[41]数据集, 详细信息见表1.

表1

Table 1

表1(Table 1)

表1 实验评估使用的模型和数据集 Table 1 Models and datasets utilized in experimental evaluation 模型 卷积层数 全连接层数 数据集 LeNet 2 3 MNIST AlexNet 5 3 CIFAR-10 VGG11 8 3 ImageNet VGG13 10 3 CelebA VGG16 13 3 ISIC2018 VGG19 16 3 Food-101 ResNet-18 17 1 ImageNet YOLO-Fastest 19 1 COCO MobileNetv1 28 1 Oxford-IIIT

表1 实验评估使用的模型和数据集 Table 1 Models and datasets utilized in experimental evaluation

为了全面评估IOP策略的性能, 选择如下两种代表性的协同推理策略进行对比实验.

1)OCP策略.最早在经典的AlexNet实验原型中采用沿输出通道维度的划分方式, 可实现多个设备的并行计算, 有效降低单个设备在模型推理过程中的内存占用及计算量.在后续的工作如CoDL和FlexFlow等, 都在划分卷积算子时采用输出通道作为划分维度.

2)CoEdge策略.在MoDNN的基础上进行改进和优化, 沿输入图像高的维度进行划分, 从数据划分层面实现推理, 降低CNN的推理时间开销.但是, 由于卷积算子滑动窗口的计算特性, 为了确保模型推理的准确性, 仍需逐算子共享输出激活的边界数据, 导致通信开销较大.

首先, 使用4张NVIDIA RTX 3090设备, 在同构场景下评估LeNet、AlexNet、VGG11在3种策略下的协同推理任务.

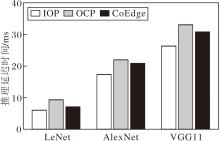
相同实验条件下3种策略对应的网络推理延迟时间测试结果如图2所示.由图可见, 对于LeNet, IOP策略分别比OCP策略和CoEdge策略节省35.34%和14.99%的推理延迟时间, 说明对于轻量级模型, IOP策略可有效减少激活值拼接带来的通信开销.对于AlexNet, IOP策略分别比OCP策略和CoEdge策略节省21.08%和16.83%的推理延迟时间.对于VGG11, IOP策略分别比OCP策略和CoEdge策略节省20.34%和14.52%的推理延迟时间.由此表明IOP策略在中等复杂度模型的协同推理任务中性能依然较优.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 3种策略下3种网络的推理延迟时间Fig.2 Inference latency of 3 networks with 3 strategies

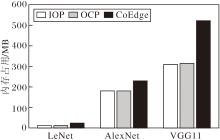
接下来, 分别评估在IOP、OCP和CoEdge策略下3种网络的峰值内存占用, 结果如图3所示.由图可见, 当整体加载划分后的模型参数并执行推理时, 对于LeNet, OCP策略与IOP策略的内存占用几乎一致, 而CoEdge策略的内存占用为24.43 MB, 几乎是OCP策略和IOP策略的两倍.对于AlexNet, 随着权重参数的增加, 3种策略的内存占用均显著上升, 其中, OCP策略和IOP策略的内存占用依然非常接近, CoEdge策略比OCP策略增加约27%的内存占用.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 3种策略下3种网络的峰值内存占用Fig.3 Peak memory usage of 3 networks with 3 strategies

由于VGG11具有更多的权重参数, 因此, 3种方案的内存开销均大幅提升, 但IOP策略的内存占用略低于OCP策略, 比CoEdge策略减少40.79%.这是由于OCP策略和IOP策略通过算子划分方式降低设备在协同推理过程中的计算开销和存储开销, 而CoEdge针对图像进行划分, 在执行推理任务的设备上部署完整的模型副本, 随着模型权重参数的增加, 会导致更大的设备内存占用.

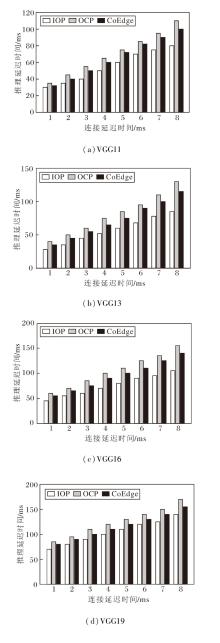
在上述实验分析中可发现, 随着模型结构的加深, 设备间的通信连接时间对协同推理的性能表现具有显著影响.为了进一步揭示该问题, 使用VGG11、VGG13、VGG16、VGG19这4种具有更深层次的VGG进行对比实验.在不同通信连接延迟场景下, 4种VGG网络在OCP、IOP、CoEdge策略下的推理延迟时间如图4所示.如图所示, 在相同的连接延迟条件下, IOP策略的推理延迟时间始终最低.对于VGG11, 当设备间连接延迟时间从1 ms增至8 ms时, IOP策略比OCP策略和CoEdge策略减少14.51%~26.74%的推理延迟时间.对于VGG13, IOP策略比OCP策略减少12.99%~24.99%推理延迟时间.这表明即使网络层次的深度略有提升, IOP策略仍能保持良好的扩展性与通信效率优势.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 3种策略下4种VGG网络的推理延迟时间Fig.4 Inference latency of 4 VGG networks with 3 strategies

对于VGG16, 虽然IOP策略在连接延迟时间较低时的优势不明显, 但在高连接延迟场景下具有明显优势, IOP策略比OCP策略降低3.34%~31.01%的推理延迟时间.对于VGG19, IOP策略比OCP策略降低15.01%~34.87%的推理延迟时间, 提升幅度最大.由此表明随着网络规模和设备间通信连接延迟时间的增加, IOP策略的优势愈加明显.

为了验证IOP策略在异构环境下的性能表现.由i9-10980XE、RTX 4090和RTX 2080Ti组成异构设备集群, 设备间连接延迟时间从1 ms增至8 ms时, 3种策略下VGG16的协同推理延迟时间如图5所示.如图所示, IOP策略比OCP策略节省约39.47%~48.28%的推理延迟时间, 表现出显著的推理性能优势.IOP策略比CoEdge策略节省约24.34%~31.82%的推理延迟时间, 说明IOP策略在异构设备条件下仍具有显著优势.

图5

Fig.5

	Figure Option ViewDownloadNew Window
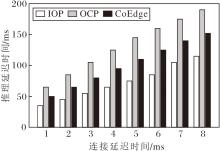	图5 4090和2080Ti组成异构场景时3种策略的推理延迟时间Fig.5 Inference latency of 3 strategies in heterogeneous environment with 4090 and 2080Ti

为了进一步验证IOP策略在异构环境下的普适性, 将NVIDIA RTX 2080Ti更换为NVIDIA GTX 1080Ti并进行评估, 结果如图6所示.如图所示, 尽管推理延迟时间有所增加, 但IOP策略依然表现出良好的扩展性.IOP策略比OCP策略减少14.29%~30.43%的推理延迟时间, 比CoEdge策略减少4.26%~20.12%的推理延迟时间.由此说明对于异构协同推理场景, IOP策略仍具有良好的适应性.随着设备集群异构性的增加, IOP策略的加速优势略有下降, 但仍显著优于OCP、CoEdge策略.

图6

Fig.6

	Figure Option ViewDownloadNew Window
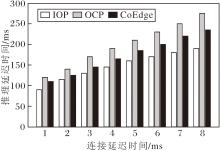	图6 4090和1080Ti组成异构场景时3种策略的推理延迟时间Fig.6 Inference latency of 3 strategies in heterogeneous environment with 4090 and 1080Ti

此外, 实验还评估链路波动环境下的容错能力.对于VGG16, OCP策略和IOP策略在链路波动状态下的推理延迟时间曲线如图7所示.

图7

Fig.7

	Figure Option ViewDownloadNew Window
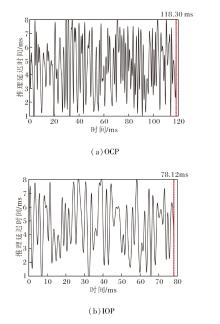	图7 链路波动状态下应用2种策略时VGG16的推理延迟时间Fig.7 Inference latency of VGG16 with 2 strategies under link fluctuation

为了更好地测试IOP在突发链路波动时的容错能力, 在持续发生链路波动时进行评估.相比OCP策略的118.30 ms, IOP策略在78.12 ms内完成推理任务, 节省33.96%的推理延迟时间.这说明IOP策略可在突发持续的链路波动状态下依然保持较好的鲁棒性和容错能力.

为了验证IOP在端侧设备上执行协同推理的效率以及模型适用的广泛性, 使用国产化平台寒武纪4芯MLU 220全国产化实验平台(如图8所示), 评估图像分类模型MobileNetv1、ResNet-18和目标检测模型YOLO-Fastest在IOP策略和OCP策略下的推理延迟时间, 结果如图9所示.

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 寒武纪4芯MLU 220全国产化平台Fig.8 Cambricon 4-chip MLU 220 fully domestic platform

图9

Fig.9

	Figure Option ViewDownloadNew Window
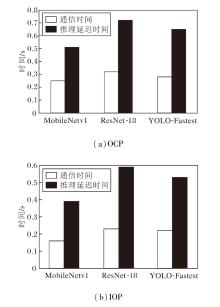	图9 寒武纪4芯MLU 220平台上2种策略的通信时间和推理延迟时间Fig.9 Communication time and inference latency of 2 strategies on Cambricon 4-chip MLU 220 platform

由图9可见, 在寒武纪4芯MLU 220平台上, 使用OCP策略时MobileNetv1的推理延迟时间为0.51 s, 其中, 推理过程中的通信时间为0.25 s, 占总推理时间的49.02%.ResNet-18的推理延迟时间为0.72 s, 其中, 推理过程中的通信时间为0.32 s, 占总推理时间的44.44%.YOLO-Fastest的推理延迟时间为0.65 s, 其中, 推理过程中通信时间为0.28 s, 占总推理时间的43.08%.在使用IOP策略时, Mobile-Netv1的推理延迟时间为0.39 s, 其中通信时间为0.16 s.ResNet-18的推理延迟时间为0.59 s, 其中通信时间为0.23 s, YOLO-Fastest的推理延迟时间为0.53 s, 其中通信时间为0.22 s.IOP策略比OCP策略节省18.06%~23.53%的推理延迟时间, 同时节省21.43%~36.00%的通信时间.由此说明IOP策略可通过减少推理过程中设备间的通信频次, 降低通信开销, 实现模型的推理加速.

由于能耗是边缘计算场景的重要性能指标之一, 因此, 基于寒武纪4芯MLU 220国产化平台, 评估Mobile-Netv1、ResNet-18、YOLO-Fastest使用IOP策略和OCP策略执行单次推理时的能耗.使用IOP策略执行推理时, Mobile-Netv1、ResNet-18和YOLO-Fastest的能耗为分别为0.28 J、0.42 J和0.38 J, 而OCP策略对应的能耗分别为0.39 J、0.55 J和0.51 J.相比OCP策略, IOP策略可节省23.64%~28.21%的能耗.由此说明IOP通过减少协同推理过程中设备间的通信频次, 在节约通信时间和推理延迟时间的同时也能有效节约系统能耗.