基于路径积分强化学习方法的蛇形机器人目标导向运动

引用本文

方勇纯, 朱威, 郭宪. 基于路径积分强化学习方法的蛇形机器人目标导向运动. 模式识别与人工智能, 2019,32(1): 1-9
FANG Yongchun, ZHU Wei, GUO Xian. Target-Directed Locomotion of a Snake-Like Robot Based on Path Integral Reinforcement Learning. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2019,32(1): 1-9. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.201901001
Permissions

《模式识别与人工智能》编辑部所有

基于路径积分强化学习方法的蛇形机器人目标导向运动

方勇纯¹, 朱威¹, 郭宪¹

1.南开大学人工智能学院机器人与信息自动化研究所天津 300350

通讯作者:方勇纯,E-mail:fangyc@nankai.edu.cn.

作者简介:

方勇纯,博士,教授,主要研究方向为机器人视觉控制、无人机、欠驱动吊车系统、微纳米操作.E-mail:fangyc@nankai.edu.cn.

朱威,硕士研究生,主要研究方向为蛇形机器人、深度强化学习.E-mail:zhuwei@mail.nankai.edu.cn.

郭宪,博士,讲师,主要研究方向为蛇形机器人、深度强化学习.E-mail:guoxian@nankai.edu.cn.

收稿日期: 2018-09-10 接受日期: 2018-12-30

资助项目: 国家自然科学基金项目(No.61603200,U1613210)资助

摘要

路径积分方法源于随机最优控制,是一种数值迭代方法,可求解连续非线性系统的最优控制问题,不依赖于系统模型,快速收敛.文中将基于路径积分强化学习的策略改善方法用于蛇形机器人的目标导向运动.使用路径积分强化学习方法学习蛇形机器人步态方程的参数,不仅可以在仿真环境下使蛇形机器人规避障碍到达目标点,利用仿真环境的先验知识也能在实际环境下快速完成相同的任务.实验结果验证方法的正确性.

关键词: 路径积分; 强化学习; 随机最优控制; 蛇形机器人; 目标导向

中图分类号:TP 242.6

Target-Directed Locomotion of a Snake-Like Robot Based on Path Integral Reinforcement Learning

FANG Yongchun¹, ZHU Wei¹, GUO Xian¹

1.Institute of Robotics and Automatic Information System, College of Artificial Intelligence, Nankai University, Tianjin 300350

Corresponding author:FANG Yongchun, Ph.D., professor. His research interests include visual control of robots, quadrotor, underactuated crane system and micro/nano manipulation.

About the Author: ZHU Wei, master student. His research interests include snake-like robot and deep reinforcement learning.

GUO Xian, Ph.D., lecturer. His research interests include snake-like robot and deep reinforcement learning.

Fund:Supported by National Natural Science Foundation of China(No.61603200,U1613210)

Abstract

Path integral is derived from stochastic optimal control. It is a numerical iteration method and solves the problem of the optimal control about continuous nonlinear systems at a high convergence speed without system model. A policy improvement algorithm based on path integral reinforcement learning is proposed for the target-directed locomotion of a snake-like robot in this paper. The path integral reinforcement learning approach is employed to learn the parameters of the snake-like robot serpentine equation, and the robot is controlled to arrive at the target position fast without contacting obstacles in simulation environment. Moreover, the robot with the priori knowledge from the simulation in real environment can complete the task well. Experimental result verifies the validity of the propose algorithm.

Key words: Key Words Path Integral; Reinforcement Learning; Stochastic Optimal Control; Snake-Like Robot; Target-Directed

文章图片

蛇形机器人的研究开始于20世纪70年代, 1972年Hirose^[1]研制第一台蛇形机器人.蛇形机器人是一种多自由度冗余机构, 因其高度的运动灵活性而适用于各种复杂环境, 如水陆两栖蛇形机器人^[2]、废墟搜救蛇形机器人^[3]、管道蛇形机器人^[4]、爬台阶蛇形机器人^[5].

由于蛇形机器人自由度较高, 因此控制非常复杂, 主要方法有:1)基于蛇形机器人步态方程控制^{[6, 7]}, 不依赖于动力学或运动学模型, 模拟生物蛇的运动(“ S曲线” 蜿蜒运动, “ 响尾蛇” 侧向运动); 2)中枢模式发生器(Central Pattern Generator, CPG)^{[8, 9]}, 同样不依赖于模型的方法, 利用中枢模式发生器的生物学概念; 3)基于运动学或动力学模型设计控制率^{[10, 11, 12]}.方法1)和2)虽然不需要模型, 但是内部参数和蛇形机器人的运动状态之间的对应关系停留在定性分析, 即参数的调整需要人为参与, 或需要经验知识, 无法精准控制, 方法3)虽然可以完全自主稳定控制, 但是目前的研究都停留在仿真环境, 难以用于实际蛇形机器人的控制.

近几年, 人工智能发展迅速, 强化学习方法广泛应用于机器人的自动控制^{[13, 14, 15]}.实验平台主要是移动机器人、机械臂等控制相对较易的机器人, 基于Q函数的强化学习方法训练规模较大, 特别引入深度信息后, 训练效率更低.基于主成分分析机器学习方法^[16]可以有效用于蛇形机器人的控制, 但是样本数据也较大.

路径积分强化学习方法基于随机最优控制理论^[17], 既不需要矩阵求逆, 也不需要梯度更新, 因此学习效率较高, 数值求解方法较稳定.路径积分强化学习方法还可用于连续非线性系统的控制^{[18, 19, 20]}.Chatterjee等^[21]利用路径积分强化学习方法, 实现带有螺旋传动单元的蛇形机器人的自动控制, 通过对参数的迭代学习, 最终完成蛇形机器人从起始点到达目标点这样一个简单任务.

本文基于路径积分强化学习方法, 学习蛇形机器人步态方程的参数, 最终实现蛇形机器人的完全自主精准控制.实验表明, 本文方法不仅能在仿真环境下控制蛇形机器人规避障碍到达目标点, 在实际实验环境中也能完成, 而且可以在很少的迭代次数内使损失函数收敛.

1 随机最优控制和路径积分

随机最优控制用于控制随机动态系统, 使性能指标函数最小.下面基于贝尔曼最优性准则(Bellman Principle of Optimality)及HJB方程分析随机最优控制和路径积分之间的关系.

性能指标函数为损失函数, 根据轨迹τ _i定义:

J(τ _i)=ϕ [x(t_N), t_N]+ $\int_{t_{i}}^{t_{N}}$ L[x(t), u(t), t]dt,

其中, t_i为初始时刻, t_N为终止时刻, x(t)为t时刻状态, u(t)为t时刻控制量, ϕ [· ]为在终止时刻t_N处损失函数, L[· ]为立即损失函数.随机最优控制目的是找到控制量u(t)并使评估函数最小:

$V_{t_{i}}$ = $\min_{u_{t_{i} ∶ t_{N}}}$ $E_{τ_{i}}$ [J(τ _i)],

其中 $E_{τ_{i}}$ [· ]为所有初始状态为 $x_{t_{i}}$ 的轨迹损失函数的期望.随机动态系统定义如下:

${\overset{\cdot}{x}}_{t}$ =f(x_t, t)+G(x_t)(u_t+ε _t),

其中, x_t∈ Rⁿ^{× 1}为系统状态量, G_t=G(x_t)∈ Rⁿ^×^p为控制矩阵, f_t=f(x_t, t)∈ Rⁿ^{× 1}为模型方程, u_t∈ R^p^{× 1}为控制向量, ε _t∈ R^p^{× 1}为协方差矩阵为Σ _ε的高斯噪声.即时回报定义如下:

L_t=L[x(t), u(t), t]=q_t+ $\frac{1}{2} {u^{T}}_{t}$ Ru_t, (1)

其中, q_t=q(x_t, t)为任意依赖于状态的损失函数, R为半正定权值矩阵.随机最优控制的HJB方程为

-∂ _tV_t=min(L_t+ $(Δ_{x} V_{t})^{T}$ F_t+ $\frac{1}{2}$ r(Δ x_xVt₎Gt_Σε ${G^{T}}_{t}$ , (2)

其中

F_t=f(x_t, t)+G(x_t)u_t.

式(1)代入式(2), 得到最优控制量:

u(x_t)=u_t=-R^-1 ${G^{T}}_{t}$ ( $Δ_{x_{t}}$ V_t), (3)

式(3)代入式(2), 得到非线性二阶偏微分方程:

-∂ _tV_t=q_t+ $(Δ_{x} V_{t})^{T}$ f_t- $\frac{1}{2} (Δ_{x} V_{t})^{T}$ G_tR^-1 ${G^{T}}_{t}$ (Δ _xV_t)+ $\frac{1}{2}$ tr((Δ _xxV_t)G_tΣ _ε ${G^{T}}_{t}$ ),

其中, Δ _x为雅克比(Jacobian)矩阵, Δ _xx为黑森(Hessian)矩阵.直接求解HJB方程很复杂, 可把HJB方程转化为线性偏微分方程, 令V_t=-λ lgΨ _t, 根据文献[17]有

-∂ _tΨ _t=- $\frac{1}{λ}$ q_tΨ _t+f ${^{T}}_{t}$ (Δ _xΨ _t)+ $\frac{1}{2} t$ r((Δ x_x_Ψt₎Gt_Σε ${G^{T}}_{t}$ , (4)

根据边界条件有

$Ψ_{t_{N}}$ =exp(- $\frac{1}{λ} ϕ_{t_{N}}$ ),

方程式(4)的解析解为

$Ψ_{t_{i}}$ = $E_{τ_{i}} (Ψ_{t_{N}}$ exp(- $\int_{t_{i}}^{t_{N}} \frac{1}{λ}$ q_tdt))= $E_{τ_{i}}$ (exp(- $\frac{1}{λ} ϕ_{t_{N}}$ 􁀄 $\frac{1}{λ} \int_{t_{i}}^{t_{N}} q_{t}$ _dt (5)

这样就把随机最优控制的问题转化为近似路径积分问题, 式(5)可转化为

$Ψ_{t_{i}}$ = $\lim_{d t \to 0}$ ∫ p(τ _i|x_i)exp[- $\frac{1}{λ}$ ( $ϕ_{t_{N}}$ + $\overset{N - 1}{\sum_{j = i}} q_{t_{j}}$ dt)]dτ _i,

其中, τ _i=( , , …, )为样本路径上的采样状态点, p(τ _i|x_i)为初始状态为x_i的样本路径τ _i的概率, 根据文献[17]有

p(τ _i|x_i)= $\frac{\exp (- \frac{1}{λ} \dot{S} (τ_{i}))}{\int \exp (- \frac{1}{λ} \dot{S} (τ_{i})) d τ_{i}}$ , (6)

其中( ${(A)}_{B}^{2}$ =A^TBA):

$\dot{S}$ (τ _i)=S(τ _i)+ $\frac{λ}{2} \overset{N - 1}{\sum_{j = i}}$ lg| $H_{t_{j}}$ |,

S(τ _i)= $ϕ_{t_{N}}$ + $\overset{N - 1}{\sum_{j = i}} q_{t_{j}}$ dt+ $\frac{1}{2} \overset{N - 1}{\sum_{j = i}} {(\frac{x_{t_{j + 1}} - x_{t_{j}}}{d t} - f_{t_{j}})}_{H_{t_{j}}^{- 1}}^{2}$ dt,

$H_{t_{j}}$ = $G_{t_{j}}$ R^-1 ${G^{T}}_{t_{j}}$ .

最优控制量: $u_{t_{i}}$ =∫ p(τ _i|x_i)u_L(τ _i)dτ _i.

式(6)概率的求解是解析解, 依赖于系统模型f_t, 可以利用路径积分方法进行数值求解, 路径积分方法不要求已知模型.在初始状态 $x_{t_{i}}$ 随机产生K条路径(τ _i_{, 1}, τ _i_{, 2}, …, τ _i_,_K), 路径τ _i_,_k的概率为

P(τ _i_,_k)= $\frac{\exp (- \frac{1}{λ} S (τ_{i, k}))}{\overset{K}{\sum_{j = 1}} \exp (- \frac{1}{λ} S (τ_{i, j}))}$ ,

其中

S(τ _i_,_k)= $ϕ_{t_{N, k}}$ + $\overset{N - 1}{\sum_{j = i}} q_{t_{j, k}}$ + $\frac{1}{2} \overset{N - 1}{\sum_{j = i}}$ (u+ $M_{t_{j, k}} ε_{t_{j, k}}$ )^TR(u+ $M_{t_{j, k}} ε_{t_{j, k}}$ ), $M_{t_{j, k}}$ = $\frac{R^{- 1} G_{t_{j, k}} {G^{T}}_{t_{j, k}}}{{G^{T}}_{t_{j, k}} R^{- 1} G_{t_{j, k}}}$ .

更新控制量:

u← u+ $\overset{K}{\sum_{k = 1}}$ P(τ _i_,_k)M $_{t_{i, k}} ε_{t_{i, k}}$ .

通过数值迭代, 最终使指标函数即损失函数收敛.

2 基于路径积分强化学习方法的蛇形机器人目标导向运动

本节使用路径积分强化学习方法优化蛇形机器人步态方程的参数.蛇形机器人步态方程的参数与其运动状态之间的模型较复杂, 理论模型在实际实验中也会存在误差, 而基于路径积分的强化学习方法可以不依赖模型, 通过端到端的训练优化参数.

2.1 蛇形机器人步态方程

Hirose^[¹^]提出蛇形机器人步态方程:

φ _i(t)=Asin(ω t+(i-1)β )+γ , (7)

其中, φ _i(t)表示t时刻第i个关节的角度.参数组

U=[ $\begin{array}{l} A & ω & β & γ \end{array}$ ]

分别表示幅值、角频率、相位和中心调整因子.A用于控制蛇形曲线的幅值角, ω 用于控制运动速度, β 用于控制蛇形曲线波的数目, γ 用于控制转弯半径.

参数组U与蛇形机器人的运动状态存在复杂的耦合关系, 理论计算的定量关系在实验过程中也会存在误差, 本文利用路径积分强化学习方法, 回避这两个问题.

2.2 路径积分强化学习

路径τ _i由控制量u_i产生, 对应的损失函数为R(τ _i), 目标是寻找控制量u, 使值函数最小:

V= $\min_{u}$ Eτ _i[R(τ _i)]= $\min_{u}$ ∫ R(τ _i)P(τ _i)dτ _i,

其中, P(τ _i)为路径τ _i对应的概率:

P(τ _i)= $\frac{S (τ_{i})}{\overset{K}{\sum_{j = 1}} S (τ_{j})}$ , (8)

其中, K表示路径总数,

S(τ _i)=exp(- $\frac{R (τ_{i}) - \min (R)}{\max (R) - \min (R)}$ )(9)

为通过R(τ _i)计算的指数损失函数,

R=[ $\begin{array}{l} R (τ_{1}) & R (τ_{2}) & \dots & R (τ_{K}) \end{array}$ ],

λ 为常数.

P(τ _i)为路径τ _i对应的概率, 同时也是产生该路径的控制量u_i占有的权重, 优化后的控制量u^*:

u^*= $\overset{K}{\sum_{i = 1}}$ P(τ _i)u_i. (10)

2.3 蛇形机器人目标导向运动

蛇形机器人目标导向运动是指控制蛇形机器人的运动, 使其到达指定位置, 文献[2]和文献[22]研究蛇形机器人的运动步态, 实现蛇形机器人的运动, 但还不能跟踪给定路径或到达给定目标点.本文使用路径积分强化学习方法, 可使蛇形机器人规避障碍到达目标点.

(x_T, y_T)为目标点位置, (x, y)为蛇形机器人头部位置, 头部初始位置为(0, 0), 使用欧氏距离表示损失函数:

R(τ _i)= $\sqrt[]{(x - x_{T})^{2} + (y - y_{T})^{2}}$ .

2.4 参数更新

路径积分强化学习方法通过迭代训练, 优化步态方程参数, 使蛇形机器人最终能从初始位置到达目标位置.步态方程参数初始值

U₀=[ $\begin{array}{l} A_{0} & ω_{0} & β_{0} & γ_{0} \end{array}$ ],

第ξ 次迭代后的参数

U_ξ=[ $\begin{array}{l} A_{ξ} & ω_{ξ} & β_{ξ} & γ_{ξ} \end{array}$ ],

每次迭代训练会随机产生K条路径, 第i条路径的随机控制量

u_i=[ $\begin{array}{l} ε_{A_{i}} & ε_{ω_{i}} & ε_{β_{i}} & ε_{γ_{i}} \end{array}$ ],

其中, ε 服从均值为0的正态分布.第ξ +1次训练第i条路径的参数:

$U_{ξ + 1}^{i}$ =U_ξ+u_i=[ $\begin{array}{l} A_{ξ} + ε_{A_{i}} & ω_{ξ} + ε_{ω_{i}} & β_{ξ} + ε_{β_{i}} & γ_{ξ} + ε_{γ_{i}} \end{array}$ ],

其中, 第i条路径对应的损失函数为R(τ _i), 第ξ +1次迭代后的参数更新为

U_ξ₊₁=U_ξ+u^*, (11)

u^*根据式(8)~式(10)计算.

ε 的方差与损失函数是相关的, 利用第ξ 次迭代后的参数U_ξ产生一条路径, 损失函数为r, 在第ξ +1次训练中ε 的标准差为

σ =f(r), (12)

其中

σ =[ $\begin{array}{l} σ_{A} & σ_{ω} & σ_{β} & σ_{γ} \end{array}$ ], f(r)=[ $\begin{array}{l} f_{A} (r) & f_{ω} (r) & f_{β} (r) & f_{γ} (r) \end{array}$ ].

2.5 算法步骤

基于路径积分强化学习方法的蛇形机器人目标导向运动算法步骤如下所示.

算法1 基于路径积分强化学习方法的蛇形机器人目标导向运动算法

初始化U₀, σ ²

for ξ =1, 2, …, M:

for i=1, 2, …, K:

根据σ ²随机产生u_i

$U_{ξ + 1}^{i}$ =U_ξ+u_i

根据式(7)产生轨迹τ _i, 对应损失函数为R(τ _i)

根据式(8)~式(11)更新参数U_ξ₊₁

利用U_ξ₊₁产生路径, 对应损失函数r, 根据式(12)更新方差

算法1给出无障碍环境下的算法, 对于有障碍环境, 需利用无障碍环境下最终训练得到的参数作为先验知识.

3 实验及结果分析

实验目的是让蛇形机器人从起始位置到达目标位置, 同时规避障碍.实验包括仿真实验和实际实验, 仿真实验包括无障碍和有障碍两种环境, 仿真物理引擎为V-REP.图1(a)为无障碍仿真环境, 图1(b)为有障碍环境, 无障碍仿真环境的训练结果为有障碍环境的训练提供先验知识.实际实验包含障碍, 如图1(c)所示, 有障碍仿真环境的训练结果为实际实验的训练提供先验知识, 在很大程度上减少实际实验训练迭代的次数.图1中3种环境的起始点和目标点位置相同, (b)和(c)中障碍物位置相同.实际蛇形机器人机构利用3D打印技术完成, 拥有8个驱动偏航关节.

	Figure Option View Download New Window
	图1 仿真和实际实验环境Fig.1 Simulated and real experiment environment

3.1 无障碍仿真实验

图1(a)为无障碍仿真环境, 蛇形机器人头部初始位置为(0, 0), 绿色目标位置

(x_T, y_T)=(1.5, 1.5),

单位为m.蛇形机器人步态方程参数初始值为

U₀=[ $\begin{array}{l} A_{0} & ω_{0} & β_{0} & γ_{0} \end{array}$ ]=[ $\begin{array}{l} \frac{2 π}{9} & 4 π & \frac{3 π}{8} & 0 \end{array}$ ],

正态分布标准差初始值为

σ ₀=[ $\begin{array}{l} σ_{A} & σ_{ω} & σ_{β} & σ_{γ} \end{array}$ ]= [ $\begin{array}{l} 0.025 & 0.5 & 0.1 & 0.02 \end{array}$ ]

迭代次数M=20, 每次迭代路径数K=30, 常数λ =30.标准差与损失函数之间的关系如下:

σ =f(r)= $\{\begin{array}{l} σ_{0}, & r \geq 0.5 \\ \frac{r σ_{0}}{2}, & 0.2 \leq r < 0.5 \\ \frac{r σ_{0}}{4}, & 0.05 \leq r < 0.2 \\ \frac{r σ_{0}}{8}, & r < 0.05 \end{array}$

仿真结果如图2所示, (a)~(d)分别对应步态方程的4个参数随着迭代次数增加的变化曲线, (e)为损失函数, (f)为第17次训练后的仿真视频.第17次训练后的参数为

U₁₇=[ $\begin{array}{l} 0.592 & 6.361 & 1.046 & - 0.064 \end{array}$ ],

损失函数r=0.135 m.

	Figure Option View Download New Window
	图2 无障碍仿真结果Fig.2 Simulation result without obstacle

3.2 有障碍仿真实验

文献[21]利用路径积分强化学习方法实现蛇形机器人在无障碍环境下到达目标位置, 在此基础上, 本文实现有障碍环境下让蛇形机器人规避障碍到达目标位置, 迭代次数相对更少.

蛇形机器人步态方程中ω 控制速度, γ 控制转弯半径, A、β 控制蛇形曲线构型.对于图1(b)的有障碍仿真环境, 可以把运动分成两段, 让蛇形机器人从两个障碍物之间穿过.初始时刻到中间时刻T_m为第一段, 步态方程参数

U⁽¹⁾=[ $\begin{array}{l} A^{(1)} & ω^{(1)} & β^{(1)} & γ^{(1)} \end{array}$ ],

中间时刻T_m到终止时刻T为第二段, 步态方程参数

U⁽²⁾=[ $\begin{array}{l} A^{(2)} & ω^{(2)} & β^{(2)} & γ^{(2)} \end{array}$ ].

这样每次迭代训练需要8个参数, 需要增加迭代次数M及路径数K, 而且无法收敛可能损失函数, 所以利用无障碍仿真实验中先验知识, 令A⁽¹⁾、β ⁽¹⁾、A⁽²⁾、β ⁽²⁾为常数, 取值为无障碍仿真实验第17次训练后对应的参数:

A⁽¹⁾=A⁽²⁾=U₁₇[1]=0.592, β (¹⁾⁼β (²⁾⁼U1_7[3]=1.046,

这样训练参数减少到4个.定义新的训练参数

$\bar{U}$ =[ $\begin{array}{l} ω^{(1)} & γ^{(1)} & ω^{(2)} & γ^{(2)} \end{array}$ ],

ω 初始值由U₁₇给定,

ω ⁽¹⁾=ω ⁽²⁾=U₁₇[2]=6.361, β ⁽¹⁾=β ⁽²⁾=0,

初始参数

${\bar{U}}_{0}$ =[ $\begin{array}{l} 6.361 & 0 & 6.361 & 0 \end{array}$ ].

新的标准差定义为

$\overset{̅}{σ}$ = [ $\begin{array}{l} {\overset{̅}{σ}}_{ω^{(1)}} & {\overset{̅}{σ}}_{ω^{(2)}} & {\overset{̅}{σ}}_{γ^{(1)}} & {\overset{̅}{σ}}_{γ^{(2)}} \end{array}$ ]

初始值

${\overset{̅}{σ}}_{0}$ =[ $\begin{array}{l} 0.5 & 0.02 & 0.5 & 0.02 \end{array}$ ],

障碍物位置

O₁=(0.25, 0.7), O₂=(0.95, 0.4),

迭代次数M=30, 路径数K=30, 中间时刻T_m=6 s, 终止时刻T=12 s, 常数λ =30.标准差和损失函数关系如下:

$\overset{̅}{σ}$ = $\bar{f}$ (r)= $\{\begin{array}{l} {\overset{̅}{σ}}_{0}, & r \geq 0.5 \\ r {\overset{̅}{σ}}_{0}, & 0.1 \leq r < 0.5 \\ \frac{r {\overset{̅}{σ}}_{0}}{2}, & r < 0.1 \end{array}$

仿真结果如图3所示, (a)~(d)分别对应步态方程的4个参数随着迭代次数增加的变化曲线, (e)为损失函数, (f)是第30次训练后的仿真视频.第30次训练后的参数

${\bar{U}}_{30}$ =[ $\begin{array}{l} 3.968 & - 0.103 & 6.510 & - 0 \end{array}$ .016],

损失函数r=0.107 m.

	Figure Option View Download New Window
	图3 有障碍仿真结果Fig.3 Simulation result with obstacles

3.3 有障碍实际实验

为了减少实际实验中迭代次数M及路径数K, 需要利用有障碍仿真实验的先验知识.实际实验训练参数

$\dot{U}$ =[ $\begin{array}{l} ω^{(1)} & γ^{(1)} & ω^{(2)} & γ^{(2)} \end{array}$ ],

初始值根据有障碍仿真实验第30次训练后的参数

${\bar{U}}_{30}$ =[ $\begin{array}{l} 3.968 & - 0.103 & 6.510 & - 0 \end{array}$ .016]

给出,

${\dot{U}}_{30}$ =[ $\begin{array}{l} 3.968 & - \frac{0.103}{3} & 6.510 & - \frac{0.016}{3} \end{array}$ ]

标准差

$\dot{σ}$ =[ $\begin{array}{l} {\overset{̅}{σ}}_{ω^{(1)}} & {\overset{̅}{σ}}_{ω^{(2)}} & {\overset{̅}{σ}}_{γ^{(1)}} & {\overset{̅}{σ}}_{γ^{(2)}} \end{array}$ ]

初始值

${\dot{σ}}_{0}$ =[ $\begin{array}{l} 0.3 & 0.008 & 0.6 & 0.008 \end{array}$ ],

障碍物位置

O₁=(0.25, 0.7), O₂=(0.95, 0.4),

迭代次数M=3, 路径数K=10, 中间时刻T_m=3 s, 终止时刻T=5.5 s, 常数λ =30.第2次迭代训练的标准差

${\dot{σ}}_{1}$ =[ $\begin{array}{l} \frac{0.3}{4} & \frac{0.008}{2} & \frac{0.6}{4} & \frac{0.008}{2} \end{array}$ ],

第3次迭代训练的标准差

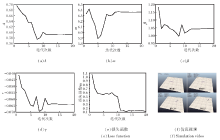
${\dot{σ}}_{2}$ =[ $\begin{array}{l} \frac{0.3}{8} & \frac{0.008}{3} & \frac{0.6}{8} & \frac{0.008}{3} \end{array}$ ],

实际实验结果如图4所示, (a)~(d)表示训练过程中每条路径随机产生的参数, (e)~(g)分别表示训练过程中第一次、第二次、第三次迭代中每条路径对应的损失函数.

在图4(e)中, 损失函数达到峰值4.243 m, 这是因为训练过程碰到障碍物.每次迭代后的参数和损失函数如表1所示, 第三次迭代后的损失函数r=0.027 m.实验结果表明, 仅需3次迭代就能使损失函数收敛.

	Figure Option View Download New Window
	图4 有障碍实际实验结果Fig.4 Experimental results with obstacles

表1 每次迭代后的参数和损失函数 Table 1 Parameters and loss function of each iteration

迭代次数	参数	损失函数r/m
$\begin{array}{l} 1 & {\dot{U}}_{1} = [4.022 - 0.042 6.968 - 0.003] & 0.048 \\ 2 & {\dot{U}}_{2} = [3.982 - 0.041 7.100 - 0.004] & 0.034 \\ 3 & {\dot{U}}_{3} = [3.966 - 0.041 7.189 - 0.004] & 0.027 \end{array}$

表1 每次迭代后的参数和损失函数 Table 1 Parameters and loss function of each iteration

3.4 结果分析

实验分成3组进行, 第1组无障碍仿真实验用到的先验知识很少, 训练参数的初始值选择随机性较强, 因此所需的迭代次数M和路径数K较大, 才能保证训练参数和损失函数的收敛.第2组有障碍仿真实验利用第1组实验训练得到的参数作为先验知识, 同时为了减少训练参数量, 选取直接影响蛇形机器人运动的2个参数ω 和γ 作为待训练的参数.因为还需要规避障碍物, 因此M和K仍然较大, 才能保证训练参数和损失函数收敛.第3组实际实验利用第2组实验训练得到的参数作为先验知识, 仅需3次迭代就能使损失函数收敛, 说明基于路径积分的强化学习方法可以较快达到收敛.

4 结束语

本文提出基于路径积分强化学习方法, 实现蛇形机器人的目标导向运动.路径积分方法源于随机最优控制, 基于贝尔曼最优性准则及HJB方程求解最优解.实验包括仿真实验和实际实验, 仿真实验分为两个部分.无障碍仿真实验的训练结果作为有障碍仿真实验的先验知识, 同时削减非直接相关的步态方程参数, 保证损失函数以较快的速度收敛.有障碍仿真的训练结果作为实际实验的先验知识, 仅需3次迭代就能使损失函数收敛到误差范围内, 这也证明路径积分强化学习方法可以不依赖机器人的运动学或动力学模型, 可以实现损失函数的收敛, 而且收敛速度较快.

参考文献

文献选项

[1]	HIROSE B S. Biologically Inspired Robots: Snake-Like Locomotors and Manipulators. Oxford, UK: Oxford University Press, 1993. [本文引用:1]
[2]	KELASIDI E, LILJEBACK P, PETTERSEN K Y, et al. Innovation in Underwater Robots: Biologically Inspired Swimming Snake Robots. IEEE Robotics and Automation Magazine, 2016, 23(1): 44-62. [本文引用:1]
[3]	BORENSTEIN J, HANSEN M, BORRELL A. The OmniTread OT-4 Serpentine Robot-Design and Performance. Journal of Field Robo-tics, 2007, 24(7): 601-621. [本文引用:1]
[4]	ROLLINSON D, CHOSET H. Pipe Network Locomotion with a Snake Robot. Journal of Field Robotics, 2014, 33(3): 322-336. [本文引用:1]
[5]	TANAKA M, NAKAJIMA M, SUZUKI Y, et al. Development and Control of Articulated Mobile Robot for Climbing Steep Stairs. IEEE/ASME Transactions on Mechatronics, 2018, 23(2): 531-541. [本文引用:1]
[6]	SATO M, FUKAYA M, IWASAKI T. Serpentine Locomotion with Robotic Snakes. IEEE Control Systems Magazine, 2002, 22(1): 64-81. [本文引用:1]
[7]	ROLLINSON D, CHOSET H. Gait-Based Compliant Control for Snake Robots // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2013: 5123-5128. [本文引用:1]
[8]	WU X D, MA S G. Adaptive Creeping Locomotion of a CPG-Controlled Snake-Like Robot to Environment Change. Autonomous Robots, 2010, 28(3): 283-294. [本文引用:1]
[9]	CRESPI A, IJSPEERT A J. Online Optimization of Swimming and Crawling in an Amphibious Snake Robot. IEEE Transactions on Robotics, 2008, 24(1): 75-87. [本文引用:1]
[10]	MATSUNO F, MOGI K. Redundancy Controllable System and Control of Snake Robots Based on Kinematic Model // Proc of the IEEE Conference on Decision and Control. Washington, USA: IEEE, 2000, V: 4791-4796. [本文引用:1]
[11]	MOHAMMADI A, REZAPOUR E, MAGGIORE M, et al. Maneuvering Control of Planar Snake Robots Using Virtual Holonomic Constraints. IEEE Transactions on Control Systems Technology, 2015, 24(3): 884-899. [本文引用:1]
[12]	ARIIZUMI R, MATSUNO F. Dynamic Analysis of Three Snake Robot Gaits. IEEE Transactions on Robotics, 2017, 33(5): 1075-1087. [本文引用:1]
[13]	OKAL B, ARRAS K O. Learning Socially Normative Robot Navigation Behaviors with Bayesian Inverse Reinforcement Learning // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2016: 2889-2895. [本文引用:1]
[14]	KRETZSCHMAR H, SPIES M, SPRUNK C, et al. Socially Compliant Mobile Robot Navigation via Inverse Reinforcement Lear-ning. International Journal of Robotics Research, 2016, 35(11): 1289-1307. [本文引用:1]
[15]	ZHU Y K, MOTTAGHI R, KOLVE E, et al. Target-Driven Visual Navigation in Indoor Scenes Using Deep Reinforcement Learning // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2017: 3357-3364. [本文引用:1]
[16]	GONG C H, TRAVERS M J, ASTLEY H C, et al. Kinematic Gait Synthesis for Snake Robots. International Journal of Robotics Research, 2016, 35(1/2/3): 100-113. [本文引用:1]
[17]	THEODOROU E, BUCHLI J, SCHAAL S. A Generalized Path Integral Control Approach to Reinforcement Learning. Journal of Machine Learning Research, 2010, 11: 3137-3181. [本文引用:2]
[18]	WILLIAMS G, DREWS P, GOLDFAIN B, et al. Aggressive Dri-ving with Model Predictive Path Integral Control // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2016: 1433-1440. [本文引用:1]
[19]	CHEBOTAR Y, KALAKRISHNAN M, YAHYA A, et al. Path Integral Guided Policy Search[J/OL]. [2018-08-23]. https://arxiv.org/pdf/1610.00529.pdf. [本文引用:1]
[20]	OKADA M, RIGAZIO L, AOSHIMA T. Path Integral Networks: End-to-End Differentiable Optimal Control[J/OL]. [2018-08-23]. https://arxiv.org/pdf/1706.09597.pdf. [本文引用:1]
[21]	CHATTERJEE S, NACHSTEDT T, WORGOTTER F, et al. Reinforcement Learning Approach to Generate Goal-Directed Locomotion of a Snake-Like Robot with Screw-Drive Units // Proc of the 23rd International Conference on Robotics in Alpe-Adria-Danube Region. Washington, USA: IEEE, 2014. DOI: DOI:10.1109/RAAD.2014.7002234. [本文引用:1]
[22]	POREZ M, IJSPEERT A J. Improved Lighthill Fish Swimming Mo-del for Bio-inspired Robots: Modeling, Computational Aspects and Experimental Comparisons. The International Journal of Robotics Research, 2014, 33(10): 1322-1341. [本文引用:1]

1993

0.0

... 蛇形机器人的研究开始于20世纪70年代,1972年Hirose^[1]研制第一台蛇形机器人 ...

2016

0.0

... 蛇形机器人是一种多自由度冗余机构,因其高度的运动灵活性而适用于各种复杂环境,如水陆两栖蛇形机器人^[2]、废墟搜救蛇形机器人^[3]、管道蛇形机器人^[4]、爬台阶蛇形机器人^[5] ...

2007

0.0

2014

0.0

2018

0.0

2002

0.0

... 由于蛇形机器人自由度较高,因此控制非常复杂,主要方法有:1)基于蛇形机器人步态方程控制^[6,7],不依赖于动力学或运动学模型,模拟生物蛇的运动(#cod#x0201c ...

2013

0.0

2010

0.0

... 2)中枢模式发生器(Central Pattern Generator, CPG)^[8,9],同样不依赖于模型的方法,利用中枢模式发生器的生物学概念 ...

2008

0.0

... 2)中枢模式发生器(Central Pattern Generator, CPG)^[8,9],同样不依赖于模型的方法,利用中枢模式发生器的生物学概念 ...

2000

0.0

... 3)基于运动学或动力学模型设计控制率^[10,11,12] ...

2015

0.0

... 3)基于运动学或动力学模型设计控制率^[10,11,12] ...

2017

0.0

... 3)基于运动学或动力学模型设计控制率^[10,11,12] ...

2016

0.0

... 近几年,人工智能发展迅速,强化学习方法广泛应用于机器人的自动控制^[13,14,15] ...

2016

0.0

... 近几年,人工智能发展迅速,强化学习方法广泛应用于机器人的自动控制^[13,14,15] ...

2017

0.0

... 近几年,人工智能发展迅速,强化学习方法广泛应用于机器人的自动控制^[13,14,15] ...

2016

0.0

... 基于主成分分析机器学习方法^[16]可以有效用于蛇形机器人的控制,但是样本数据也较大 ...

2010

0.0

... 路径积分强化学习方法基于随机最优控制理论^[17],既不需要矩阵求逆,也不需要梯度更新,因此学习效率较高,数值求解方法较稳定 ...

... _t,根据文献[17]有 ...

2016

0.0

... 路径积分强化学习方法还可用于连续非线性系统的控制^[18,19,20] ...

0.0

... 路径积分强化学习方法还可用于连续非线性系统的控制^[18,19,20] ...

0.0

... 路径积分强化学习方法还可用于连续非线性系统的控制^[18,19,20] ...

2014

0.0

... Chatterjee等^[21]利用路径积分强化学习方法,实现带有螺旋传动单元的蛇形机器人的自动控制,通过对参数的迭代学习,最终完成蛇形机器人从起始点到达目标点这样一个简单任务 ...

2014

0.0