基于最优投影平面的立体视觉空间圆位姿高精度测量方法

引用本文

李政源, 马昕, 李贻斌. 基于最优投影平面的立体视觉空间圆位姿高精度测量方法. 模式识别与人工智能, 2019,32(1): 58-66
LI Zhengyuan, MA Xin, LI Yibin. An Optimal Projection Plane-Based Spatial Circle Measurement Method Using Stereo Vision System. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2019,32(1): 58-66. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.201901008
Permissions

《模式识别与人工智能》编辑部所有

基于最优投影平面的立体视觉空间圆位姿高精度测量方法

李政源¹, 马昕¹, 李贻斌¹

1.山东大学控制科学与工程学院机器人研究中心济南250061

通讯作者:

马昕,博士,教授,主要研究方向为人工智能、机器视觉、移动机器人.E-mail:maxin@sdu.edu.cn.

作者简介：

李政源,硕士研究生,主要研究方向为视觉感知.E-mail:lizhengyuan@mail.sdu.edu.cn.

李贻斌,博士,教授,主要研究方向为机器人学、智能控制理论.E-mail:liyb@sdu.edu.cn.

收稿日期: 2018-12-15 接受日期: 2019-01-04

资助项目: 国家自然科学基金和山东省人民政府联合基金项目(No.U1706228)、国家自然科学基金项目(No.61673245)、山东省重点研发计划(重大关键技术)项目(No.2016ZDJS02A07)资助

摘要

现有基于双目立体视觉的测量方法的测量精度依赖于标定精度,在受遮挡时测量精度不高.文中首先分析并证明在双目立体视觉系统外部参数误差存在时,投影曲线上点的立体匹配误差对点的重建精度的影响.然后基于此误差分析结论,设计立体视觉空间圆位姿测量方法,通过轮廓点筛选算法筛选投影曲线上的点,得到匹配误差较小的点并进行重建.利用重建点在深度方向上对非线性优化得到最优投影平面的投影,对空间圆进行拟合,得到空间圆的位置姿态.文中方法有效减小三维点重建误差对空间圆拟合精度的影响,提高圆形特征在受遮挡情况下的测量精度.最后通过实验验证方法的有效性.

关键词: 立体视觉; 空间圆; 位姿; 非线性优化

中图分类号:TP 391.4

An Optimal Projection Plane-Based Spatial Circle Measurement Method Using Stereo Vision System

LI Zhengyuan¹, MA Xin¹, LI Yibin¹

1. Center for Robotics, School of Control Science and Engineering, Shandong University, Ji'nan 250061

Corresponding author:MA Xin, Ph.D., professor. Her research interests include artificial intelligence, machine vision and mobile robots.

About the Author:LI Zhengyuan, master student. His research interests include visual perception.

LI Yibin, Ph.D., professor. His research interests include robotics and intelligent control theories.

Fund:Supported by the Joint Fund of National Natural Science Foundation of China and Shandong Province(No. U1706228), National Natural Science Foundation of China(No.61673245), Key Research Plan of Shandong Province (No.2016ZDJS02A07)

Abstract

The accuracy of the existing measurement method based on binocular stereo vision depends on the accuracy of calibration, and the accuracy of measurement decreases when the spatial circle is occluded. Firstly, the reconstruction accuracy of point affected by the stereo matching error of points on projection curves is analyzed in the presence of external parameter error of the binocular stereo vision system. Then, based on the conclusion of error analysis, a new method for measuring the position and orientation of spatial circle is designed. Using the edge points selecting algorithm, the points of projection curves are selected. The circle is then reconstructed using the points with small stereo matching error. The projection of the reconstructive points on the optimal projection plane based on nonlinear optimization in the direction depth is utilized for fitting spatial circle to obtain the position and orientation. Experimental results prove the effectiveness of the proposed algorithm.

Key words: Key Words Stereo Vision; Spatial Circle; Position and Orientation; Nonlinear Optimization

文章图片

空间中的圆在工业生产环境中大量存在^{[1, 2, 3]}, 如工件上的圆形安装孔、螺栓孔等.在工业现场, 机器人需要完成大量的装配工作, 如安装螺栓、汽车轮胎的自动夹装.除上述工业环境中的应用, 关于空间圆形特征的视觉定位算法在无人系统的导航和定位中也有大量的应用^[4].空间圆的位置和姿态的测量是机器视觉方向的一个重要问题^[5].

一般来说, 空间圆位姿的测量方法可分为两类:1)基于结构光传感器的主动测量方法, 通过结构光传感器和相机组建立体视觉系统^{[6, 7, 8]}; 2)基于双目立体视觉系统的被动测量方法, 利用两个相机组建立体视觉系^{[9, 10, 11, 12, 13, 14, 15, 16, 17, 18]}.相比主动测量方法^[9], 被动测量方法的测量速度更快^[10].相比结构光传感器, 相机的体积更小, 重量更轻, 造价更低.在工业现场中, 工业机器人的承载能力有限, 双目视觉系统的优势更突出.

目前, 基于双目立体视觉系统的空间圆位姿测量方法可分为3种.

1)基于代数射影几何的方法, 通过投影与曲面之间的几何约束, 得到空间圆位姿的闭式解.Safaee-Rad等^[11]利用二次曲面的射影性质, 给出二次曲线的全局匹配和重建算法, 通过求解高阶多项式方程得到空间圆的位姿.Quan^[12]基于空间圆是两视图中的二次曲线确定的二次曲面的交线的性质, 给出更简单的位姿计算方法, 可以判断两个视角中二次曲线的对应关系.Xu等^[13]也通过类似的方法实现空间圆位姿的测量.此类方法具有非常严谨的数学推理, 在理想的状态下测量精度较高.但是在实际应用中, 不可避免产生图像噪声、边缘提取误差、相机标定误差, 计算方法复杂, 矩阵之间的运算导致误差进一步扩大.上述原因可能会导致测量值不精确, 甚至得不到有效解.

2)基于计算机辅助设计(Computer Aided Design, CAD)模型的先验信息和双目立体视觉系统相结合的方法, 可以准确提取孔边缘, 减少边缘提取误差, 得到更精确的测量结果^[14].Malassiotis 等^[15]设计基于CAD模型的汽车零件自动检测算法, 依靠双目立体视觉传感器和先验知识, 解决空间中几何孔边缘提取问题和高精度测量问题, 对光线干扰具有较强的鲁棒性.但是, 此类方法十分依赖孔的CAD模型, 在几何孔被遮挡时, 很难检测到部分孔被遮挡的情况.

3)利用双目立体视觉系统求出空间圆边缘点的三维空间坐标, 并利用三维坐标信息拟合空间圆, 求取空间圆的位姿.文献[16] 、文献[17] 设计空间圆最优拟合方法, 将拟合误差分为两部分:重建点到空间圆平面的距离, 以及重建点到拟合圆心的距离与拟合半径的差为拟合误差, 两者之和最小时得到空间圆的最优拟合结果.Chen等^[18] 设计利用新的非切线约束的方法, 提高椭圆上点的立体匹配精度和空间圆位姿的测量精度.相比代数射影几何方法及基于CAD模型的先验信息和双目立体视觉系统结合的方法, 此类方法不需要过多的先验信息, 计算过程简单, 测量精度较高.但是, 当空间圆部分轮廓受遮挡时, 由于相机外参标定误差的必然存在, 重建得到的边缘点在深度方向上的误差会随匹配误差的增大而迅速增大, 大幅影响算法的测量精度.

针对上述问题, 本文分析椭圆边缘的立体匹配误差的变化规律和此误差对边缘重建精度的影响, 设计基于最优投影平面的空间圆位姿测量算法.首先设计可以反映最优投影平面位置的误差函数, 利用重建得到的空间圆边缘三维点在深度方向上对最优投影平面的投影, 减小双目立体视觉系统外部参数误差的影响.然后设计轮廓点筛选方法, 通过对轮廓点所在曲线的斜率筛选轮廓点, 可筛除重建误差较大的无参考意义的边缘点, 利用筛选后的边缘点对空间圆进行拟合, 有效提高测量精度.最后通过实验证明本文算法在空间圆受遮挡时仍具有较高的位姿测量精度.

1 数学模型

1.1 双目立体视觉系统模型

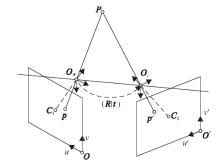
2个相机组成的双目立体视觉系统的模型和相应的空间三维点投影关系如图1所示^[¹⁹^].设世界坐标系为O_WX_WY_WZ_W, 与左相机坐标系重合.左图像坐标系为Ouv, 焦距为f₁.右相机坐标系为O_rX_rY_rZ_r, 图像坐标系为O'u'v', 焦距为f₂.通过对双目立体视觉系统的标定, 可得到两相机内部参数矩阵:

A₁= $[\begin{array}{l} \frac{f_{1}}{d X_{1}} & 0 & u_{0} \\ 0 & \frac{f_{1}}{d Y_{1}} & v_{0} \\ 0 & 0 & 1 \end{array}]$ , A2₌ $[\begin{array}{l} \frac{f_{2}}{d X_{2}} & 0 & u'_{0} \\ 0 & \frac{f_{2}}{d Y_{2}} & v'_{0} \\ 0 & 0 & 1 \end{array}]$

其中, dX₁、dY₁为左相机像元的物理尺寸, dX₂、dY₂为右相机像元的物理尺寸, (u₀, v₀)、(u'₀, v'₀)分别为左右相机图像平面上的主点坐标.

同时得到外部参数矩阵:旋转矩阵R和平移向量t.

	Figure Option View Download New Window
	图1 双目视觉系统示意图Fig.1 The schematic diagram of binocular vision system

如图1所示, 设空间中视野内有一点

P= ${[\begin{array}{l} X & Y & Z \end{array}]}^{T}$ ,

在左、右两相机图像平面上的投影分别为

p= ${[\begin{array}{l} u & v \end{array}]}^{T}$ , p'= ${[\begin{array}{l} u' & v' \end{array}]}^{T}$ ,

两者的关系可表示为

λ ₁ $[\begin{array}{l} u \\ v \\ 1 \end{array}]$ =A₁ $[\begin{array}{l} X \\ Y \\ Z \\ 1 \end{array}]$ , (1)

λ ₂ $[\begin{array}{l} u' \\ v' \\ 1 \end{array}]$ =A₂(R|t) $[\begin{array}{l} X \\ Y \\ Z \\ 1 \end{array}]$ , (2)

其中λ ₁、λ ₂为尺度因子.

在已知双目立体视觉系统内外参数和空间点在左右图像中对应的图像坐标的条件下, 通过式(1)和式(2)可以解得该点空间坐标.

1.2 立体匹配

通过左右图像中点的投影恢复空间中点的实际位置, 必须对左右视图上的图像点进行立体匹配.一般来说, 立体重构算法分为密集型重构算法和特征型重构算法^[²⁰^].密集型重构算法对两幅图像中的所有匹配点进行重构, 一般使用基于区域的匹配方法, 在参考图像中某像素点的周围给定一个特定大小的区域, 依据一定的相似性判断准则, 在待匹配图像中寻找与参考区域最相似的子区域.该子区域对应的像素点即为对应的匹配点, 但算法对低纹理区域和重复纹理区域的匹配效果并不理想.特征型重构算法只重构某些特征的空间位置, 通过边缘检测算法对图像中的椭圆边缘进行提取和筛选, 仅对筛选的边缘进行立体匹配和重构, 可满足空间圆位姿测量的实际需要.

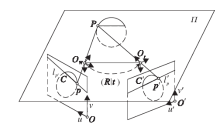
具体匹配方法如图2所示, 空间中有一圆形, 投影到左、右两图像上, 通过轮廓提取算法提取和筛选图像上的椭圆轮廓, 得到两图像上的椭圆轮廓C和C'.假设左图椭圆轮廓上存在一个像点p, 通过已知的相机内外参数可以得到极平面Π 的位置, 极平面Π 与右图像平面交于极线l'_p, 极线l'_p与右图椭圆轮廓相交, 根据顺序一致性约束可以得到像点p在右图上的匹配点p'.通过极线约束的特征型重构算法对左、右图像椭圆轮廓上的像点进行立体匹配, 重构空间圆边缘点的空间位置P.立体匹配算法降低匹配算法的复杂性, 提高匹配速度.相比密集型重构算法, 大幅减少匹配点的数量, 提高算法效率.

	Figure Option View Download New Window
	图2 对极几何Fig.2 Epipolar geometry

2 误差分析

在实际应用中, 由于双目立体视觉系统外部参数误差的存在, 导致使用极线约束对椭圆轮廓进行立体匹配时, 产生立体匹配误差, 影响空间圆边缘点的重建精度, 从而影响空间圆的拟合精度.为了进一步提高空间圆位姿测量的精度, 在双目立体视觉系统外部参数误差存在时, 分析空间圆边缘重建产生的影响.

2.1 外部参数误差对曲线上点的立体匹配误差的影响

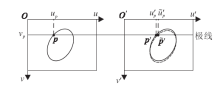
双目视觉系统经过标定之后, 为了方便进行立体匹配, 通常进行图像校正^[²¹^].经过图像校正, 可以将一般的双目模型转化到一个理想的模型, 即像平面在同一平面, 且光轴与像平面垂直, 两视图的极线相互平行.并且当空间中的一点投影到两像平面时, 两点像素在同一行, 一般称此时的两相机共面行对准.如图3所示, 在理想状态下, 空间圆在图像平面上的投影为两实线椭圆, 两视图椭圆上的点一一对应, 通过计算匹配点的视差可以得到该点的深度信息.但由于外部参数误差, 经过图像校正后, 空间中一点在两图像平面上的投影并不一定在同一行, 这使曲线上的点通过极限约束进行立体匹配时, 会产生立体匹配误差.

	Figure Option View Download New Window
	图3 椭圆边缘的立体匹配误差Fig.3 Stereo matching error of elliptical edge

为了方便误差的分析, 假设两相机内部参数均不存在误差, 并且外部参数误差只对左图中曲线的位置产生影响, 如图3所示, 图中实线椭圆为理想条件下的空间圆投影, 通常在双目立体视觉系统外部参数误差存在时, 校正后的图像会产生某个方向的偏移和轻微变形, 这里将变形忽略.如图4所示.

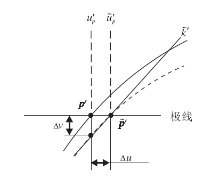
	Figure Option View Download New Window
	图4 立体匹配误差与曲线斜率的关系Fig.4 Relationship between stereo matching error and the slope of curve

设图像发生某个方向上的偏移, 将偏移分解为横纵两个方向, 纵向偏移量为Δ v, 方向向下, 图中实曲线为理想外参数据下校正得到的边缘曲线投影, 虚曲线为实际校正后得到的边缘曲线投影, 极线与理想边缘曲线和实际边缘曲线分别交于点p'(v'_p, u'_p)和点 $\dot{p}$ '( $\dot{v}$ '_p, $\dot{u}$ '_p), 则匹配点的横坐标误差为Δ u.

定理1 在双目立体视觉系统中, 通过极线约束对曲线上的点进行立体匹配时, 随着图像上曲线的斜率 $\dot{k}$ '变小, 得到的匹配点的横坐标误差Δ u会变大.

证明由图3所示, 点p的实际视差 ${\dot{d}}_{p}$ 为点 $\dot{p}$ '与点p的横坐标的差:

${\dot{d}}_{p}$ = $\dot{u}$ '_p-u=d_p+Δ u,

视差的误差为Δ u.

由图4可知, 将斜率 $\dot{k}$ '近似看作点 $\dot{p}$ '处的曲线斜率, 可知

$\dot{k}$ '≈ $\frac{Δv}{Δu}$ ,

其中Δ v为定值.则由上式可知, Δ u与 $\dot{k}$ '为负相关, 即随着图像上曲线的斜率变小, 所得匹配点 $\dot{p}$ '的横坐标误差Δ u会变大.

2.2 立体匹配误差对三维点重建精度的影响

如图5所示, 两相机为共面行对准, 焦距为f, 坐标系位置与前文所述一致.设空间中有一点

P= ${[\begin{array}{l} X & Y & Z \end{array}]}^{T}$ ,

在左右摄像机图像平面上的投影分别为点p(u_p, v_p)、 p'(v'_p, u'_p).

	Figure Option View Download New Window
	图5 立体匹配误差对点重建精度的影响Fig.5 Influence of stereo matching error on accuracy of point reconstruction

定理2 点的立体匹配误差越大, 重建的三维点坐标误差就会越大, 并且该点Z坐标的误差大于X和Y坐标的误差.

证明假设左右相机经过标定, 焦距f、基线长度b已知, 且不存在误差, 则由三角形的相似性可得到P点的坐标为

Z=h= $\frac{b}{u'_{p} - u_{p}}$ f= $\frac{b}{d_{p}}$ f, (3)

X= $\frac{h}{f}$ v_p₌ $\frac{b}{d_{p}}$ p_, Y= $\frac{h}{f}$ =v_p $\frac{b}{d_{p}}$ , (4)

其中, d_p=u'_p-u_p为视差.

由2.1节可知, 在双目立体视觉系统外参误差存在时, 通过极线约束对图像上曲线进行立体匹配, 容易产生视差的误差Δ u, 即易匹配到点.如图5所示, 此时点P的Z坐标误差为

Δ Z=Z- $\dot{Z}$ =bf/d_p-bf/ ${\dot{d}}_{p}$ =bf（ ${\dot{d}}_{p}$ -d_p）/d_p ${\dot{d}}_{p}$ , (5)

其中

${\dot{d}}_{p}$ = $\dot{u}$ '_p-u_p, Δ ${\dot{d}}_{p}$ dp_-dp₌ $\dot{u}$ p_-up_-u'p₊up₌Δ u.(6)

根据式(3)、式(5)、式(6)可得,

Δ Z=Z- $\dot{Z}$ =（dp ${\dot{d}}_{p}$ ）^-¹bf bf $\frac{Δu}{bf} = \frac{\overset{⌢}{ZZ}}{bf}$ Δ u≈ $\frac{Z^{2}}{bf}$ Δ u.(7)

由式(7)可知, 点P的Z坐标误差Δ Z与点P的深度的平方成正比, 空间点的距离越远, 空间点的深度误差越大.类似地, 基线长度和相机焦距越大, 空间点的深度误差越小.

根据几何知识和式(4)、式(7), 点P的X坐标误差为

Δ X= $\frac{ΔZ}{f}$ u_p≈ $\frac{Z^{2}}{bf} \frac{u_{p}}{f}$ Δ u= $\frac{Z}{bf} \frac{Z u_{p}}{f}$ Δ u= $\frac{ZX}{bf}$ Δ u , (8)

不失一般性, 在实际场景中, X总是小于Z, 故由式(7)、式(8)可知, Δ X小于Δ Z.

类似地, 点P的Y坐标误差为

Δ Y= $\frac{ΔZ}{f}$ v_p≈ $\frac{Z^{2}}{bf} \frac{v_{p}}{f}$ Δ u= $\frac{Z}{bf} \frac{Z v_{p}}{f}$ Δ u= $\frac{ZY}{bf}$ Δ u .(9)

同理, 在实际场景中, Y总是小于Z, 故由式(7)、式(9)可知, Δ Y小于Δ Z.

由式(7)~式(9)可知, 图像上点的立体匹配误差越大, 重建得到的三维点坐标误差就会越大, 并且该点Z坐标的误差要大于X、Y坐标的误差.

通过上述证明, 可知在常见的双目测量方法中, 通过极线约束对图像上曲线上的点进行立体匹配时, 点所在的曲线的斜率越小, 立体匹配的误差越大, 所得三维点坐标重建精度越低, 特别是Z坐标的重建精度, 低于X、Y坐标.

3 空间圆位姿高精度测量算法

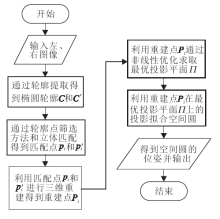
在双目立体视觉系统的外参误差必然存在的情况下, 重建得到的边缘点的Z坐标误差是影响空间圆拟合精度的关键.为了减小Z坐标误差对拟合精度的影响, 本文提出基于最优投影平面的空间圆位姿测量算法.图6为本文算法的流程图.

	Figure Option View Download New Window
	图6 本文算法流程图Fig.6 Flow chart of the proposed method

3.1 边缘检测和轮廓提取

使用Canny边缘提取算法^[²²^]对左、右视图中的圆形特征进行边缘检测, 利用轮廓曲率和长度等性质筛选视图中的轮廓, 筛除不是椭圆形的边缘, 通过文献[12]中的椭圆轮廓匹配算法, 可以得到两视图中来自于同一空间圆映射的两椭圆轮廓C和C'.

3.2 立体匹配和三维重建

通过本文设计的轮廓点筛选方法, 筛选提取的图像中的椭圆轮廓.筛选后的椭圆轮廓通过极线约束建立左右图像轮廓上点的对应匹配关系, 根据三角法计算每个点的三维坐标.

由第2节分析可知, 随着曲线C在轮廓点p_i处的斜率降低, 重建得到的边缘点P_i在Z方向的坐标误差Δ Z大幅增加, 与之同时, 边缘点P_i在X、Y方向的坐标误差Δ X和Δ Y也随之增加.通过筛选轮廓点可以避免重建误差较大的边缘点参与空间圆的拟合, 在提高测量精度的同时, 也减少点的重建数量, 提高计算效率.

本文提出立体轮廓点的筛选方法, 以左视图提取得到的曲线C'在轮廓点p'_i处的斜率大小k'_p'作为筛选条件, 可以筛除重建误差较大的无参考意义的边缘点, 留下重建精度较高的边缘点.首先对曲线C'进行求导, 得到曲线上各点的斜率k'_p, 然后设定阈值K, 只有当|k'_p|> K时才允许右图上的点与该点进行立体匹配.本文方法可以将边缘点的重建误差限制在某一范围内, 经过大量实验, 当阈值K=3时, 既能保证边缘点的数量不至于太少, 又能保证边缘点的重建误差不至于太大.

设通过轮廓点筛选方法得到的左图像上的点为p'_j, 基于1.2节方法, 利用极线约束进行立体匹配, 可以得到右图像上与p'_j相对应的匹配点p_j.之后利用三角法^[²³^]对立体匹配得到的匹配点进行三维重建, 得到空间圆上的部分点P_j的三维坐标.

3.3 最优投影平面计算

设空间圆的圆心坐标为O_C= ${[\begin{array}{l} x_{C} & y_{C} & z_{C} \end{array}]}^{T}$ , 半径为r, 则空间圆所在平面Π 的方程可表示为

n· (ξ -O_C)=0, (10)

其中, n为平面Π 的单位法向量, ξ = ${[\begin{array}{l} x & y & z \end{array}]}^{T}$ 为平面Π 上的任意点.

对于空间圆上任意一点X_i=(x_i, y_i, z_i), 满足如下条件:

$|X_{i} - O_{C}|$ =r,

且满足式(10).令重建后得到的边缘点为P_i(i=1, 2, …, n), 由2.2节分析可知, 当图像中曲线斜率变小时, P_i在Z方向的坐标误差显著增大.假设P_i在Z方向的误差Δ Z远大于其在X、Y方向的误差Δ X、Δ Y, 那么, 可将Δ X、Δ Y忽略, 即

Δ X≈ 0, Δ Y≈ 0, Δ Z≫0.

由于Δ Z≫0, 导致本应在平面Π 上的点P_i脱离平面Π .通过点P_i在Z方向上对平面Π 进行投影, 得到投影点P'_i.P'_i的X、Y坐标近似于真实值, P'_i在平面Π 上, 即此时投影点P'_i的Z方向的误差Δ Z'最小.

设点P'_i在平面Π 上的圆形拟合误差表示为

ε = $\overset{n}{\sum_{i = 1}} {(|P_{i} - O_{C}| - r)}^{2}$ .

由上述可知, 点P'_i在平面Π 上的圆形拟合误差约等于0.

综上所述, 当边缘点P_i的X、Y方向的误差可以忽略时, 点P_i在深度方向对平面Π 的投影P'_i的圆形拟合误差最小.将平面Π 称为最优投影平面, 根据这一特性, 本文设计求取最优投影平面的计算方法, 具体过程如下.

1)选择一个初始平面Π ⁰, 该平面的法向量为n⁰.

2)将得到的三维点P_i= $(x_{i}, y_{i}, z_{i})^{T}$ 在Z方向向平面Π ⁰投影, 得到三维点

P'_i= $(x'_{i}, y'_{i}, z'_{i})^{T}$ , i=1, 2, …, n.

3)通过三维点P'_i在平面Π ⁰上拟合平面圆C⁰, 得到C⁰的圆心O⁰=( $x_{C}^{0}$ , $y_{C}^{0}$ , $z_{C}^{0}$ ), 半径为r⁰.

4)计算误差函数

ε ⁰= $\overset{n}{\sum_{i = 1}} (\sqrt[]{(x'_{i} - x_{C}^{0})^{2} + (y'_{i} - y_{C}^{0})^{2}} - r^{0})^{2}$ .

5)通过L-M非线性优化方法, 求得最优投影平面Π .

算法的关键在于初值选取, 本文利用筛选得到空间圆重建点, 使用最小二乘法拟合空间平面的法向量作为初值平面Π ⁰的法向量, 并计算右图曲线上斜率最大的轮廓点.利用该点的三维重建精度最高的特点, 使Π ⁰始终通过该像点重建得到的边缘点.实验验证表明, 这种初值选择方法是合理的, 可以迅速收敛到最优值.

3.4 空间圆的拟合

通过3.3节中分析可知, 将空间点P_i在Z方向上对平面Π 进行投影, 得到投影点P'_i.P'_i的X、Y坐标近似于真实值, 且点P'_i的Z方向的误差Δ Z'最小.所以此时通过投影P'_i对空间圆进行拟合, 得到空间圆的几何参数的误差也最小.将三维点P'_i转化成平面Π 上的二维点, 利用最小二乘法对圆形进行拟合, 得到空间圆的半径和圆心, 将二维平面上的圆心转化为三维空间中的点, 即可得到空间圆圆心的三维位置, 圆面的法向量为最优投影平面Π 的法向量.

4 实验及结果分析

为了验证双目立体视觉系统外参误差对空间圆边缘重建精度产生的影响和算法的有效性, 下面开展一系列的仿真实验和真实实验.

4.1 仿真实验

利用计算机生成一个共面行对准的双目立体视觉系统和空间圆, 其中, 世界坐标系与左相机坐标系重合, 右相机的光心在世界坐标系中的坐标为(0.5, 0, 0), 两相机内部参数相同, 内参矩阵为

A= $[\begin{array}{l} \frac{f}{dX} & 0 & u_{0} \\ 0 & \frac{f}{dY} & v_{0} \\ 0 & 0 & 1 \end{array}]$ = $[\begin{array}{l} \frac{8}{4 \times 10^{- 6}} & 0 & 1000 \\ 0 & \frac{8}{4 \times 10^{- 6}} & 750 \\ 0 & 0 & 1 \end{array}]$ ,

外部参数为

R= $[\begin{array}{l} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}]$ , t= $[\begin{array}{l} 0.5 \\ 0 \\ 0 \end{array}]$ .

首先通过此模型验证本文误差分析的正确性.设有一空间圆半径r=0.3 m, 圆心位于O_C= , 投影到两相机的成像平面, 并对投影中加入高斯噪声, 模拟实际实验中的图像噪声, 对外部参数矩阵(R|t)加入旋转和平移误差, 模拟双目立体视觉系统标定产生的误差.通过本文方法, 利用生成投影和双目立体视觉系统的内外参数, 重建空间圆, 得到的空间圆重建边缘点和空间圆真实边缘点在三维空间中的位置, 如图7所示.利用重建边缘点P_i与真实边缘点的坐标相减得到各方向的坐标误差Δ X、Δ Y和Δ Z, 以及重建点P_i的各方向坐标误差Δ X、Δ Y和Δ Z与图像上曲线在对应点p'的倾角的关系.

	Figure Option View Download New Window
	图7 空间圆重建边缘点和真实边缘点的位置Fig.7 The reconstructed edge points and real edge points of spatial circle

图8为重建边缘点P_i的误差与图像上曲线在对应点p'_i 的倾角的关系.由图可以发现, 在匹配点所在位置曲线的倾角接近90° (即曲线的斜率变大)时, 重建边缘点的各方向坐标误差Δ X、Δ Y和Δ Z逐渐趋近于0.在匹配点所在位置曲线的倾角接近0° 或180° (即曲线斜率变小)时, Δ X、Δ Y和Δ Z迅速变大, 且误差Δ Z大于Δ X、Δ Y.此次实验结果不失一般性, 多次实验结果均与第2节所分析的重建误差变化规律结论基本一致.

	Figure Option View Download New Window
	图8 重建边缘点P_i的误差与图像上曲线在对应点p’_i 的倾角的关系Fig.8 The relationship between the error of point P_i and the angle of inclination

为了验证算法的有效性, 通过空间圆位姿测量的仿真实验检验算法的有效性.在同样的环境配置下, 将空间圆位姿测量实验分为受遮挡时和不受遮挡时两组.通过最小二乘法拟合空间圆、文献[13]算法与本文算法进行对比, 对比测量值与真实值, 得到空间圆的圆心位置误差、半径误差和圆面法向量角度误差.每组进行20次实验, 计算误差的均值.

表1和表2分别给出空间圆不受遮挡和受遮挡时的实验结果.从表1可以看出, 本文算法在空间圆不受遮挡时, 虽然法向量精度提升效果不明显, 但圆形位置测量精度和半径测量精度明显优于其它对比算法.当空间圆受遮挡时, 3种算法的测量精度均有所下降, 而本文算法仍能得到较高的测量精度.

表1 仿真环境下不受遮挡时空间圆的实验结果 Table 1 Experimental results of the spatial circle without occlusion in simulation environment

表2 受遮挡时空间圆的实验结果 Table 2 Experimental results of the spatial circle with occlusion

4.2 真实实验

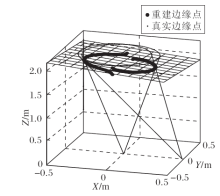
为了验证本文算法的有效性, 采用两台型号为MER-200-14GC的CCD相机和两个焦距为16 mm的镜头组成一个双目立体视觉系统, 对距离为2 m左右、直径为80 cm的汽车轮胎轮毂进行测量.图9为实验场景.

	Figure Option View Download New Window
	图9 真实实验环境Fig.9 The real experiment environment

在同样的实验环境下, 分为轮毂受遮挡时和不受着遮挡时两组实验.通过最小二乘法拟合空间圆、文献[13]算法与本文算法进行对比.对轮毂的中心在图像中的像点进行三维重建, 得到的坐标为轮毂圆心的真实值, 与轮毂面重合的标定板的法向量为轮毂法向量的真实值, 通过与真实值对比得到轮毂的圆心位置相对误差、半径误差和圆面法向量角度误差.每组20次实验, 计算误差的均值.表3和表4列出实验结果.

表3 真实环境下轮毂不受遮挡时的实验结果 Table 3 Experimental results of the hub without occlusion in real environment

表4 真实环境下轮毂受遮挡时的实验结果 Table 4 Experimental results of the hub with occlusion in real environment

实验表明, 在真实实验中, 由于相机内部参数的标定(如焦距和畸变系数等)误差的存在, 以及轮毂边缘的提取存在偏差, 相比仿真实验, 本文算法的精度略有下降.在轮毂不受遮挡时, 本文算法的精度明显高于最小二乘法和文献[13]算法.在轮毂受到遮挡时, 其它两种方法的精度均产生下降, 而本文算法仍能得到较高的测量精度.

5 结束语

本文提出基于最优投影平面的立体视觉空间圆位姿测量算法, 通过对提取的椭圆轮廓点进行筛选, 获得立体匹配精度较高的匹配点, 经过三维重建后使用三维点在最优投影平面上的投影对空间圆进行拟合.相比其它测量方法, 本文方法考虑双目立体系统外部参数标定误差对轮廓点重建精度的影响, 在空间圆受遮挡或不受遮挡时, 测量精度更优.未来将看重于本文算法应用到实际工厂环境中, 并进一步检验算法有效性.

参考文献

文献选项

[1]	LUHMANN T. Close Range Photogrammetry for Industrial Applications. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(6): 558-569. [本文引用:1]
[2]	DENIZ C, CAKIR M. In-Line Stereo-Camera Assisted Robotic Spot Welding Quality Control System. Industrial Robot: An International Journal, 2018, 45(1): 54-63. [本文引用:1]
[3]	LEE Y, LEE S. Object Recognition and Pose Estimation Based on 3D Planar Closed Loop Boundaries // Proc of the IEEE International Conference on Automation Science and Engineering. Washington, USA: IEEE, 2016: 245-250. [本文引用:1]
[4]	EBERLI D, SCARAMUZZA D, WEISS S, et al. Vision Based Position Control for MAVs Using One Single Circular Land mark. Journal of Intelligent and Robotic Systems, 2011, 61(1/2/3/4): 495-512. [本文引用:1]
[5]	PERKINS W A. INSPECTOR: A Computer Vision System that Learns to Inspect Parts. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1983, 5(6): 584-592. [本文引用:1]
[6]	WU B, XUE T, YE S H. A Two-Step Method for Spatial Circle Orientation with a Structured Light Vision Sensor and Error Analysis. Measurement Science and Technology, 2010, 21(7). DOI: DOI:10.1088/0957-0233/21/7/075105. [本文引用:1]
[7]	GAO Y, SHAO S Y, FENG Q B. A New Method for Dynamically Measuring Diameters of Train Wheels Using Line Structured Light Visual Sensor // Proc of the Symposium on Photonics and Optoelectronics. Washington, USA: IEEE, 2012. DOI: DOI:10.1109/SOPO.2012.6270922. [本文引用:1]
[8]	GONG Z, SUN J H, ZHANG G J. Dynamic Structured-Light Measurement for Wheel Diameter Based on the Cycloid Constraint. Applied Optics, 2016, 55(1): 198-207. [本文引用:1]
[9]	MA X, FENG J B, LI Y B, et al. Active 6-D Position-Pose Estimation of a Spatial Circle Using Monocular Eye-in-Hand System. International Journal of Advanced Robotic Systems, 2018, 15(1). DOI: DOI:10.1177/1729881417753692. [本文引用:2]
[10]	HU Y Q, MA Y, XU M, et al. Measurement Algorithm of Mounting Holes Based on Binocular Stereo Vision // Proc of the IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems. Washington, USA: IEEE, 2016: 489-492. [本文引用:2]
[11]	SAFAEE-RAD R, TCHOUKANOV I, SMITH K C, et al. Three-Dimensional Location Estimation of Circular Features for Machine Vision. IEEE Transactions on Robotics and Automation, 1992, 8(5): 624-640. [本文引用:2]
[12]	QUAN L. Conic Reconstruction and Correspondence from Two Views. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(2): 151-160. [本文引用:2]
[13]	XU W F, XUE Q, LIU H D, et al. A Pose Measurement Method of a Non-cooperative GEO Spacecraft Based on Stereo Vision // Proc of the 12th International Conference on Control Automation Robotics and Vision. Washington, USA: IEEE, 2012: 966-971. [本文引用:3]
[14]	LOWE D G. Fitting Parameterized Three-Dimensional Models to Images. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(5): 441-450. [本文引用:2]
[15]	MALASSIOTIS S, STRINTZIS M G. Stereo Vision System for Precision Dimensional Inspection of 3D Holes. Machine Vision and Applications, 2003, 15(2): 101-113. [本文引用:2]
[16]	周富强, 张广军, 江洁. 空间圆几何参数的非接触高精度测量方法. 仪器仪表学报, 2004, 25(5): 604-607. (ZHOU F Q, ZHANG G J, JIANG J. High Accurate Non-contact Method for Measuring Geometric Parameters of Spatial Circle. Chinese Journal of Scientific Instrument, 2004, 25(5): 604-607. [本文引用:2]
[17]	ZHOU F Q, WANG Y X, PENG B, et al. A Novel Way of Understand ing for Calibrating Stereo Vision Sensor Constructed by a Single Camera and Mirrors. Measurement, 2013, 46(3): 1147-1160. [本文引用:2]
[18]	CHEN X, LIN G Y. Wheel Center Detection Based on Stereo Vi-sion. Journal of Southeast University(English Edition), 2013, 29(2): 175-181. [本文引用:2]
[19]	ZHANG Z Y. Determining the Epipolar Geometry and Its Uncertainty: A Review. International Journal of Computer Vision, 1998, 27(2): 161-195. [本文引用:1]
[20]	SCHARSTEIN D, SZELISKI R. A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms. International Journal of Computer Vision, 2002, 47(1/2/3): 7-42. [本文引用:1]
[21]	STEGER C, ULRICH M, WIEDEMANN C. Machine Vision Algorithms and Applications. New York, USA: Wiley, 2008. [本文引用:1]
[22]	CANNY J. A Computational Approach to Edge Detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986 8(6): 679-698. [本文引用:1]
[23]	HARTLEY R I, STURM P. Triangulation. Computer Vision and Image Understand ing, 1997, 68(2): 146-157. [本文引用:1]

2010

0.0

... 空间中的圆在工业生产环境中大量存在^[1,2,3],如工件上的圆形安装孔、螺栓孔等 ...

2018

0.0

... 空间中的圆在工业生产环境中大量存在^[1,2,3],如工件上的圆形安装孔、螺栓孔等 ...

2016

0.0

... 空间中的圆在工业生产环境中大量存在^[1,2,3],如工件上的圆形安装孔、螺栓孔等 ...

2011

0.0

... 除上述工业环境中的应用,关于空间圆形特征的视觉定位算法在无人系统的导航和定位中也有大量的应用^[4] ...

1983

0.0

... 空间圆的位置和姿态的测量是机器视觉方向的一个重要问题^[5] ...

2010

0.0

... 一般来说,空间圆位姿的测量方法可分为两类:1)基于结构光传感器的主动测量方法,通过结构光传感器和相机组建立体视觉系统^[6,7,8] ...

2012

0.0

... 一般来说,空间圆位姿的测量方法可分为两类:1)基于结构光传感器的主动测量方法,通过结构光传感器和相机组建立体视觉系统^[6,7,8] ...

2016

0.0

... 一般来说,空间圆位姿的测量方法可分为两类:1)基于结构光传感器的主动测量方法,通过结构光传感器和相机组建立体视觉系统^[6,7,8] ...

2018

0.0