定义1 三元组(U, A, I)称为一个形式背景, 其中, U={x₁, x₂, …, x_n}为对象集, A={a₁, a₂, …, a_m}为属性集, I⊆U× A为U与A之间的二元关系.对∀ x∈ U, a∈ A, (x, a)∈ I表示对象x具有属性a, (x, a)∉I表示对象x不具有属性a.

定义2 设(U, A, I)为形式背景, 对x∈ U, a∈ A, X⊆U, B⊆A, 定义

x^* ={a|a∈ A, (x, a)∈ I},

a^* ={x|x∈ U, (x, a)∈ I},

X^◇={a∈ A|a^* ∩ X≠ Ø },

B^□={x∈ U|x^* ⊆B},

其中, x^* 表示对象x具有的属性集合, a^* 表示具有属性a的对象集合, X^◇表示X中的对象具有的属性集合, B^□表示只具有B中属性的对象集合.特别地, 记{x}^◇=x^◇, {a}^□=a^□.

若对∀ x∈ U, 有x^* ≠ Ø , x^* ≠ A, 并且对于∀ a∈ A, 有a^* ≠ Ø , a^* ≠ U, 则称形式背景(U, A, I)是正则的.

注意到, X^◇= ∪x∈Xx^◇, 易知{x^◇|x∈ U}为{X^◇|X⊆U}的并式生成组.

定义3 设(U, A, I)为形式背景, 对X⊆U和B⊆A, 若X=B^□且B=X^◇, 则称二元组(X, B)为一个面向属性概念, 其中, X为面向属性概念的外延, B为面向属性概念的内涵.

用_PL(U, A, I)表示形式背景(U, A, I)的全体面向属性概念, 对

(X₁, B₁)∈ _PL(U, A, I), (X₂, B₂)∈ _PL(U, A, I),

定义

(X₁, B₁)≤ (X₂, B₂)⇔ X₁⊆X₂⇔ B₁⊆B₂,

并称(X₂, B₂)为(X₁, B₁)的父概念, (X₁, B₁)为(X₂, B₂)的子概念, 则_PL(U, A, I)为一个偏序集.

在_PL(U, A, I)上定义

(X₁, B₁)∧ (X₂, B₂)=(X₁∩ X₂, (B₁∩ B₂ )□◇), (X1_, B1₎∨ (X2_, B2₎=((X1_∪ X2 )◇□B1_∪ B2₎,

则(_PL(U, A, I), ∨ , ∧ )为一个完备格.若

(X₁, B₁)≤ (X₂, B₂)

且不存在(X, B)∈ _PL(U, A, I), 使得

(X₁, B₁)≤ (X, B)≤ (X₂, B₂),

则称(X₂, B₂)为(X₁, B₁)的真父概念, (X₁, B₁)为(X₂, B₂)的真子概念.

对于知识结构(Q, K)和能力结构(S, ), 当给定问题集Q和技能集S时, 直接称K为知识结构, 为能力结构.

设(Q, K)为知识结构:若K满足并封闭, 则称(Q, K)为知识空间; 若K满足交封闭, 则称(Q, K)为简单闭包空间.

设(Q, K)为知识结构, 对于q∈ Q, K_q表示K中包含问题q的知识状态构成的集族.记

[q]={r∈ Q|K_q=K_r},

[q]表示与q同时出现在某些知识状态中的问题构成的集合.若对∀ q∈ Q, [q]为单点集, 则称(Q, K)为一个可辨识的知识结构.

无特殊说明的情形下, 本文讨论的知识结构均为可辨识的.

定义4 三元组(Q, S, μ )称为一个技能函数, 其中, Q为非空问题集, S为非空技能集, μ 为由Q到 22S\{Ø}\{Ø }的映射, 且对∀ q∈ Q, μ (q)内的元素两两不可比较.

当给定问题集Q和技能集S时, 直接称μ 为一个技能函数.

对∀ q∈ Q, C∈ μ (q)称为解决问题q的极小能力, 即表示学习者至少需要掌握C中的全部技能才足以解决问题q.对技能子集T⊆S, 定义

K={q∈ Q|∃C∈ μ (q), C⊆T},

称K是由T通过技能函数μ 诱导得到的知识状态.遍历S的所有子集, 得到所有知识状态构成的集族K, 称(Q, K)为由技能函数μ 确定的知识结构.

在技能函数(Q, S, μ )中, 对∀ q∈ Q, 满足

1)μ (q)≠ Ø ;

2)对∀ M∈ μ (q), M≠ Ø ;

3)μ (q)内的能力关于集合的包含关系两两不可比较.

设(Q, S, μ )为技能函数,

1)若对∀ q∈ Q, μ (q)={M}, 其中Ø ⊂M⊆S, 则称(Q, S, μ )为一个合取技能函数.合取技能函数确定的知识结构满足交封闭, 是一个简单闭包空间.

2)若对∀ q∈ Q, μ (q)={{s}:s∈ M}, 其中Ø ⊂M⊆S, 则称(Q, S, μ )为一个析取技能函数.析取技能函数确定的知识结构满足并封闭, 是一个知识空间.

设(Q, S, μ )为合取技能函数, 可表示为三元组(Q, S, τ ), 其中, τ 为由Q到2^S的映射, 满足:对∀ q∈ Q, 有μ (q)={τ (q)}.对∀ q∈ Q, τ (q)⊆S表示分配给问题q的极小能力.此时, 对于T⊆S, T通过合取技能函数τ 诱导得到的知识状态可表示为

K={q∈ Q|τ (q)⊆T}.

在无特殊说明的情形下, 后文均用(Q, S, τ )表示合取技能函数.

定义5 设G, G'分别为2个集族.若G'包含G中所有有限个元素的并组成的集合, 则称集族G'为G的张成, 记为S(G)=G', 或称G张成G'.

定义6 设F为一个集族, 若对∀ K∈ F, L∈ F, 存在有限序列

K=K₀, K₁, …, K_p=L,

使K_i-1与K_i之间的距离

d(K_i-1, K_i)=|(K_i-1\K_i)∪ (K_i\K_i-1)|=1,

其中, 1≤ i≤ p, p=d(K, L), 则称F是良级的.

本文称满足定义6的有限序列

K=K₀, K₁, …, K_p=L

是由K到L的紧路径.若F是良级的, 则F是满足良级性的.

本文视问题为对象、技能为属性.设(Q, S, τ )合取技能函数, 对于q∈ Q, s∈ S, 根据关系

s∈ τ (q)⇔ (q, s)∈ I,

合取技能函数(Q, S, τ )可转换为形式背景(Q, S, I), 称这样的形式背景为技能背景.在技能背景(Q, S, I)中, 对∀ q∈ Q, 有q^◇=τ (q).

引理1 设(Q, S, I)是与合取技能函数(Q, S, τ )对应的技能背景, 对∀ (K, T)∈ _PL(Q, S, I), T通过τ 诱导得到的知识状态为K, 记

K={K|(K, T)∈ _PL(Q, S, I)},

则K是由τ 诱导得到的简单闭包空间.

证明 对于(K, T)∈ _PL(Q, S, I), 有

K=T^□, T=K^◇,

而

T^□={q∈ Q|q^* ⊆T}

且

q^* ={s∈ S| (q, s)∈ I}=τ (q).

显然, 对∀ q∈ Q, 有q^* =τ (q), 于是

K={q∈ Q|τ (q)⊆T},

也就是说T通过合取技能函数τ 诱导得到的知识状态为K.

由于面向属性概念格_PL(Q, S, I)所有外延构成的集族是满足交封闭的, 于是_PL(Q, S, I)中所有面向属性概念外延构成的集族即为合取技能函数(Q, S, τ )诱导得到的简单闭包空间.证毕.

设(Q, S, I)为与合取技能函数(Q, S, τ )对应的技能背景, 若(Q, K)是由τ 诱导得到的知识结构, 也称(Q, K)为技能背景(Q, S, I)确定的知识结构.

定理1 设(Q, S, I)为技能背景, 对∀ (K, T)∈ _PL(Q, S, I), T为2^S中诱导知识状态K的最小能力状态.

证明 设T'⊂T⊆S也诱导知识状态K, 则

K={q∈ Q|τ (q)⊆T'⊂T}={q∈ Q|τ (q)⊂T},

也就是存在s∈ T但s∉T', 对∀ q∈ K, s∉τ (q), 否则τ (q)⊈T'.因此对∀ q∈ K, 技能s与问题q的求解无关, 故s^* ∩ K=Ø , 这与T=K^◇矛盾.综上所述, T是2^S中诱导知识状态K的极小能力状态.证毕.

记

={T| (K, T)∈ _PL(Q, S, I)},

{q^◇|q∈ Q}为的并式生成组, 也就是说可由{q^◇|q∈ Q}张成得到.显然满足并封闭, 且Ø ∈ , S∈ , 于是(S, )为能力空间, 且称(S, )是由技能背景(Q, S, I)确定的能力空间.显然对∀ (K, T)∈ _PL(Q, S, I), 知识状态为K的学习者至少掌握T中的所有技能.于是可得如下结论.

推论1 设(Q, S, I)为技能背景, 对∀ (K, T)∈ _PL(Q, S, I), 知识状态为K的学习者的最小能力状态为T.

定理2 设(Q, S, I)为技能背景, (S, )为由(Q, S, I)确定的能力空间.对_PL(Q, S, I)中任意一对真父子概念(K₁, T₁)≤ (K₂, T₂), 有|T₂-T₁|=1当且仅当是良级的.

证明 ⇒ .对∀ T∈ , T'∈ , 不妨设T⊆T', 由_PL(Q, S, I)是一个完备格可知, 存在K⊆Q, K'⊆Q, 使(K, T)≤ …≤ (K', T').显然存在由T到T'的紧路径.

若T⊈T', 且T≠ Ø , T'≠ Ø , 则存在

(Ø , Ø )≤ …≤ (K, T), (Ø , Ø )≤ …≤ (K', T'),

即存在由T到Ø 的紧路径和由Ø 到T'的紧路径.也就是说存在由T到T'的紧路径.综上所述, 是良级的.

⇐.对_PL(Q, S, I)中任意一对真父子概念(K₁, T₁)≤ (K₂, T₂), 显然有|T₂-T₁|=1.否则若|T₂-T₁|> 1, 由是良级的可知, 存在T∈ , 使T₁⊂T⊂T₂, 于是存在(K, T)∈ _PL(Q, S, I)使得

(K₁, T₁)≤ (K, T)≤ (K₂, T₂),

这与(K₁, T₁)为(K₂, T₂)的真子概念矛盾.证毕.

定义10 设(Q, S, I)为技能背景, (S, )为由(Q, S, I)确定的能力空间.对于q∈ Q, 若q^◇为T中包含技能s的极小能力状态, 则记q↙s.

定理3 设(Q, S, I)为技能背景, (S, T)为由(Q, S, I)确定的能力空间.对于_PL(Q, S, I)中任意一对真父子概念(K₁, T₁)≤ (K₂, T₂), 有|T₂-T₁|=1当且仅当对∀ q∈ Q, 至多存在一个技能s∈ S使得q↙s.

证明 ⇒ .假设存在q∈ Q, s∈ S, t∈ S, 使得q↙s且q↙t, 即q^◇是包含技能s和技能t的极小内涵.存在K⊆Q, 使得(K, q^◇)∈ _PL(Q, S, I).设(K', T)为(K, q^◇)的真子概念, 由T⊆q^◇且s∉T, t∉T, 得|q^◇-T|> 1, 矛盾.

⇐.对∀ (K, T)∈ _PL(Q, S, I), 用n表示(K, T)在面向属性概念格的哈斯图中的层数, 且(Ø , Ø )在第1层.当n=2时, 显然存在q∈ Q, 使T=q^◇, 因此|T-Ø |=1.假设n≤ m, 当2< m≤ |S|时, (K, T)有x(x≥ 1)个真子概念(K₁, T₁), (K₂, T₂), …, (K_x, T_x), 且|T-T_i|=1, i=1, 2, …, x.由此可知, T_i两两之间只有一个技能不同, 于是(K, T)所在的层中所有面向属性概念内涵两两之间也只有一个技能不同.因此当n=m+1, 2< m≤ |S|时, 对(K, T)的任意真子概念(K', T'), 有|T-T'|=1.因此, 对_PL(Q, S, I)中任意一对真父子概念(K₁, T₁)≤ (K₂, T₂), 有|T₂-T₁|=1.证毕.

定理4 设(Q, S, I)为技能背景, (S, )为由(Q, S, I)确定的能力空间.为良级的当且仅当对∀ q∈ Q, 至多存在一个技能s∈ S, 使得q↙s.

证明 由定理2和定理3可证得. 证毕.

根据真父子概念的定义可知, 在技能背景(Q, S, I)中, 对_PL(Q, S, I)中任意一对真父子概念(K₁, T₁)≤ (K₂, T₂), K₂为知识状态K₁的后继状态.

推论2 设(Q, S, I)为与合取技能函数(Q, S, τ )对应的技能背景, (S, )是由(Q, S, I)确定的能力空间, 是良级的当且仅当(Q, S, τ )是良好的.

是由{q^◇|q∈ Q}通过张成得到的, 故只需在{q^◇|q∈ Q}中寻找包含技能s∈ S的极小能力状态.设(Q, S, τ )是与技能背景(Q, S, I)对应的合取技能函数, 若(Q, S, τ )是良好的, 也称技能背景(Q, S, I)是良好的.

推论3 设(Q, S, I)是良好的技能背景, 对_PL(Q, S, I)中任意一对真父子概念(K₁, T₁)≤ (K₂, T₂), s∈ (T₂-T₁)为由K₁到K₂的有效技能.

例1 给定合取技能函数(Q₁, S₁, τ ), 其中,

Q₁={1, 2, 3, 4, 5, 6}, S₁={a, b, c, d}, τ (1)={a}, τ (2)={b}, τ (3)={a, c}, τ (4)={b, c, d}, τ (5)={a, c, d}, τ (6)={b, c}.

由关系

s∈ τ (q)⇔ (q, s)∈ I

可得到与合取技能函数(Q₁, S₁, τ )对应的技能背景(Q₁, S₁, I).对∀ s∈ S₁, 在{q^◇|q∈ Q₁}中寻找包含技能s的极小能力状态, 从而得到带↙的技能背景(Q₁, S₁, I), 如表1所示.其中, 对于q∈ Q₁, s∈ S₁, ↙表示q↙s.0表示(q, s)∉I, 1表示(q, s)∈ I.

表1

Table 1

表1(Table 1)

表1 带↙的技能背景表(Q1, S1, I) Table 1 Skill context (Q1, S1, I) with ↙ Q1\S1 a b c d 1 ↙ 0 0 0 2 0 ↙ 0 0 3 1 0 ↙ 0 4 0 1 1 ↙ 5 1 0 1 ↙ 6 0 1 ↙ 0

表1 带↙的技能背景表(Q1, S1, I) Table 1 Skill context (Q1, S1, I) with ↙

由表1可知, 对∀ q∈ Q₁, 至多存在一个技能s∈ S₁使得q↙s.{q^◇|q∈ Q₁}通过张成得到

={Ø , {a}, {b}, {a, c}, {a, b}, {b, c}, {a, c, d},

{b, c, d}, {a, b, c}, S₁},

于是能力空间是良级的.

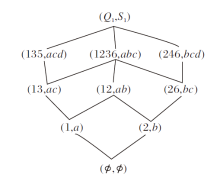
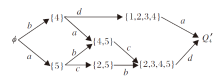
通过计算得到技能背景(Q₁, S₁, I)的面向属性概念格_PL(Q₁, S₁, I), 如图1所示.图中面向属性概念(135, acd)表示能力状态{a, c, d}诱导的知识状态为{1, 3, 5}, 说明知识状态为{1, 3, 5}的学习者的最小能力状态为{a, c, d}.由图1可知合取技能函数(Q₁, S₁, τ )确定的知识结构为

K={Ø , {1}, {2}, {1, 3}, {1, 2}, {2, 6}, {1, 3, 5}, {2, 4, 6}, {1, 2, 3, 6}, Q₁}.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 面向属性的概念格PL(Q1, S1, I)Fig.1 Property oriented concept lattice PL(Q1, S1, I)

给定技能背景(Q, S, I), 可确定知识结构(Q, K)和能力空间(S, ).显然|K|=||, 且K中的知识状态与中的能力状态是一一对应的.也就是说对∀ K∈ K, 都能在中找到诱导K的唯一的最小能力状态.

定理5 设(Q, S, I)为良好的技能背景.对∀ (K, T)∈ _PL(Q, S, I), K≠ Q, 设(K, T)存在x(x≥ 1)个真父概念(K₁, T₁), (K₂, T₂), …, (K_x, T_x).若知识状态为K的学习者的能力状态为T_K, 则T⊆T_K, 且对∀ s∈ ∪i=1, 2, …, x(T_i-T), 有s∉T_K.

证明 由推论1可知, 知识状态为K的学习者的最小能力状态为T, 即T⊆T_K.

若x=1, 即(K, T)只有一个真父概念(K₁, T₁).

由(Q, S, I)是良好的, 可设T₁-T={s}.显然s∉T_K, 否则学习者的知识状态为K₁.同理若x≥ 1, 可得对∀ s∈ ∪i=1, 2, …, x(T_i-T), 有s∉T_K.证毕.

特别地, 若学习者的知识状态为K=Q, 则其能力状态为S.

若(Q, S, I)为良好的技能背景, 则能力结构

={T| (K, T)∈ _PL(Q, S, I)}

是良级的, 此时对于K∈ K(K≠ Q), 存在K的后继状态, 且存在由K到其任意后继状态的有效技能.从而可保证学习者只需学习一个有效技能便可改变原有的知识状态, 且可根据学习者的知识状态是否发生改变来推断其是否掌握相应的有效技能.

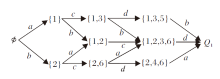
例2 续例1, 技能背景(Q₁, S₁, I)确定的能力空间T是良级的, 即(Q₁, S₁, I)是良好的.对∀ K∈ K, K≠ Q₁, 存在由K到其后继状态的有效技能.如图1所示, 对真父子概念(13, ac)≤ (135, acd), {1, 3, 5}为{1, 3}的后继状态, 且由推论3得技能d是由{1, 3}到{1, 3, 5}的有效技能.从而得到技能集S₁的学习路径图如图2所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 技能集S1的学习路径图Fig.2 Learning paths diagram for skill set S1

由图2可知, 技能b、c都是知识状态{1}到其后继状态的有效技能.知识状态为{1}的学习者通过学习技能b能达到知识状态{1, 2}, 通过学习技能c能达到知识状态{1, 3}.另外, 得到处于K中任意知识状态的学习者对技能的掌握情况如表2所示.表中K× s表示知识状态为K的学习者没有掌握技能s, K$\surd$s表示知识状态为K的学习者掌握技能s.例如, 知识状态为{1, 3, 5}的学习者掌握技能a、c、d, 没有掌握技能b.

表2

Table 2

表2(Table 2)

表2 (Q1, K)中知识状态的技能掌握情况 Table 2 Skill mastery of knowledge state in (Q1, K) K\S1 a b c d Ø × × {1} $\surd$ × × {2} × $\surd$ × {1, 2} $\surd$ $\surd$ × {1, 3} $\surd$ × $\surd$ × {2, 6} × $\surd$ $\surd$ × {1, 3, 5} $\surd$ × $\surd$ $\surd$ {2, 4, 6} × $\surd$ $\surd$ $\surd$ {1, 2, 3, 6} $\surd$ $\surd$ $\surd$ × Q $\surd$ $\surd$ $\surd$ $\surd$

表2 (Q1, K)中知识状态的技能掌握情况 Table 2 Skill mastery of knowledge state in (Q1, K)

设(Q, S, I)为技能背景, 其确定的知识结构为(Q, K), 能力空间为(S, ).若不是良级的, 也就是说(Q, S, I)不是良好的, 此时对K∈ K, K≠ Q, 不一定存在由K到其后继状态的有效技能.知识状态为K的学习者可能学习并掌握某些技能但知识状态却无法改变, 这将无法通过学习者对问题的回答情况以评估其是否掌握相应技能.

对s∈ S, 用δ (s)表示包含技能s的极小能力状态构成的集族.若T不是良级的, 说明存在q∈ Q, s∈ S, t∈ S, s≠ t, 使得q↙s且q↙t.也就是说, q^◇∈ δ (s)且q^◇∈ δ (t).考虑添加问题, 使得对∀ s'∈ S, s'≠ s, s'≠ t, δ (s')保持不变, 且q^◇∉δ (s)或q^◇∉δ (t).也就是说, 通过添加问题, 使得新得到的技能背景表中每行至多只存在一个↙.

定理6 设(Q, S, I)为技能背景.对于q∈ Q, 若存在s∈ S, t∈ S, 使得q^◇∈ δ (s)且q^◇∈ δ (t), 则增加满足如下2个条件的问题p, 不改变δ (s'), s'∈ S, s'≠ s, s'≠ t, 且使得q^◇∉δ (s)或q^◇∉δ (t).

1)p^◇⊂q^◇, 且s∈ p^◇或t∈ p^◇;

2)对∀ s'∈ p^◇, s'≠ s, s'≠ t, B∈ δ (s'), 有B⊂p^◇.

证明 当q^◇={s, t}, 不妨设p^◇={t}, 显然问题p满足1)、2)条件.新增问题p后不改变δ (s'), s'∈ S, s'≠ s, s'≠ t.因为p^◇⊂q^◇, 所以p^◇∈ δ (t)且q^◇∉δ (t).

当q^◇⊃{s, t}时, 不妨设q^◇={s, t, s'}, 取p^◇={t, s'}, 显然p满足1)、2)条件.新增问题p后, 由于对∀ B∈ δ (s'), 有B⊂p^◇, 即p^◇∉δ (s'), 因此δ (s')不改变, s'∈ S, s'≠ s, s'≠ t.同理因为p^◇⊂q^◇, 所以q^◇∉δ (t).

综上所述, 定理成立.证毕.

对于q∈ Q, 定理6讨论的是存在2个技能s∈ S, t∈ S, 使得q^◇是包含s和t的极小能力状态的情形.而实际上, 可能存在多个技能, 使q^◇是包含这些技能的极小能力状态.

推论4 设(Q, S, I)为技能背景.对于q∈ Q, 若存在s₁∈ S, s₂∈ S, …, s_m∈ S, 2≤ m≤ |S|, 使得q^◇∈ δ (s_i), i=1, 2, …, m, 则添加满足以下两个条件的m-1个问题p_j, j=1, 2, …, m-1, 不改变δ (s'), s'∈ S, s'≠ s_i, i=1, 2, …, m, 且使得存在唯一的i∈ {1, 2, …, m}, 使q^◇是包含s_i的极小能力状态.

1) pj◇⊂q^◇, 且存在唯一的i∈ {1, 2, …, m}, 使得s_i∈ pj◇;

2)对∀ s'∈ pj◇, s'≠ s_i, i=1, 2, …, m, B∈ δ (s'), 有B⊂ pj◇.

给定技能背景(Q, S, I), 其确定的能力空间为.若不是良级的, 即技能背景(Q, S, I)不是良好的, 也就是说存在q∈ Q, 使得q^◇是包含多个技能的极小能力状态.根据定理6和推论4, 可通过添加问题, 使得对∀ q∈ Q, 至多存在一个技能s∈ S, 使得q↙s.

下面给出寻找良好技能背景的算法1.

算法1 获取良好的技能背景

输入 技能背景(Q, S, I)

输出 良好的技能背景(Q', S, I')

step 1 对∀ s∈ S, 在{q^◇|(q, s)∈ I, q∈ Q}中寻找δ (s).

step 2 对∀ q∈ Q, 计算

Ω (q)={s|q^◇∈ δ (s)}.

step 3 若对∀ q∈ Q, |Ω (q) |≤ 1, 则跳转step 4; 否则记

ξ '=ξ ={Ω (q):q∈ Q, |Ω (q) |> 1},

其中ξ (ξ ')按Ω (q)的基数从大到小进行排列, 并执行如下操作.

FOR i=2 to |ξ '| DO

IF |ξ '(i)- ∪j=1, 2, …, i-1(ξ '(j)∩ ξ '(i)) |≤ 1

THEN

ξ (i)← Ø ;

ELSE

ξ (i)← ξ '(i)- ∪j=1, 2, …, i-1(ξ '(j)∩ ξ '(i));

END IF

END FOR

FOR i=1 to |ξ | DO

α =|ξ (i) |-1;

Q← Q∪ {q_|Q|+1, q_|Q|+2, …, q_|Q|+α },

q_|Q|+i(i=1, 2, …, α )满足推论4;

END FOR

step 4 Q'← Q, I'⊆Q'× S, 获得技能背景(Q', S, I').

例3 给定合取技能函数(Q₂, S₂, τ ), 其中,

Q₂={1, 2, 3, 4}, S₂={s, t, u, v}, τ (1)={t, u}, τ (2)= {s, u, v}, τ (3)={t}, τ (4)={u}.

与(Q₂, S₂, τ )对应的技能背景(Q₂, S₂, I)如表3所示.

表3

Table 3

表3(Table 3)

表3 技能背景(Q2, S2, I) Table 3 Skill context (Q2, S2, I) Q2\S2 s t u v 1 0 1 1 0 2 1 0 1 1 3 0 1 0 0 4 0 0 1 0

表3 技能背景(Q2, S2, I) Table 3 Skill context (Q2, S2, I)

经计算, 得

δ (s)=δ (v)={2^◇}, δ (t)={3^◇}, δ (u)={4^◇}.

也就是说对于2∈ Q₂, s∈ S₂, v∈ S₂满足2↙s与2↙v, 故技能背景(Q₂, S₂, I)不是良好的.

根据定理6, 添加问题5, 其中5^◇={s, u}.此时, Q'₂=Q₂∪ {5}, I'⊆Q'₂× S₂, 得到新的技能背景(Q'₂, S₂, I').在技能背景(Q'₂, S₂, I')中, 对∀ q∈ Q'₂, 至多存在一个技能, 使得q^◇是包含它的极小能力状态.也就是说(Q'₂, S₂, I')是良好的技能背景.

给定技能背景(Q, S, I), 其确定的知识结构为(Q, K).对∀ K∈ K, K≠ Q, 寻找K的所有后继状态及达到其后继状态需学习的技能, 从而得到技能集S的所有学习路径.

当(Q, S, I)是良好的技能背景时, 对∀ K∈ K, K≠ Q, 由K到其每个后继状态都只需要学习一个技能, 从而根据学习路径图可有效指导学习, 并评估学习者是否掌握相应的有效技能.下面给出基于技能背景寻找学习路径图的算法2.

算法2 基于技能背景获取学习路径图

输入 技能背景(Q, S, I)

输出 学习路径图G

step 1 给定一个空图G.

step 2 ∂ ← Ø , ρ ← Ø , 其中∂ 表示G中所有边的集合, ρ 表示G中所有学习路径.

step 3 {q^◇|q∈ Q}张成得到.

step 4 计算K={{q∈ Q|q^◇⊆T}:T∈ }.

step 5 令i=1, 2, …, |K|-1, j∈ {1, 2, …, |K|}, 执行如下操作:

IF K(j)是K(i)的后继状态 THEN

∂ ← ∂ ∪ (K(i), K(j)), 其中(K(i), K(j))是由K(i)指向K(j)的边, 边的标记为(j)-(i);

END IF

step 6 根据∂ 找出所有学习路径ρ , 画出学习路径图G.

例4 续例3, 在技能背景(Q₂, S₂, I)中, 对{1^◇, 2^◇, 3^◇, 4^◇}张成得到

={Ø , {t}, {u}, {t, u}, {s, u, v}, S₂}.

通过计算得(Q₂, S₂, I)确定的知识结构为

K={Ø , {3}, {4}, {1, 3, 4}, {2, 4}, Q₂},

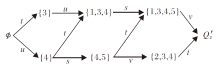
并得到在技能背景(Q₂, S₂, I)下技能集S₂的学习路径图, 如图3所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 (Q2, S2, I)下S2的学习路径图Fig.3 Learning paths diagram for S2 in (Q2, S2, I)

由图3可知, 由知识状态{4}到{2, 4}及由知识状态{1, 3, 4}到Q₂不存在有效技能.知识状态为{4}或{1, 3, 4}的学习者通过学习并掌握技能s或v并不能有效改变其原有的知识状态.

例3中通过添加问题5得到良好的技能背景(Q'₂, S₂, I').对{1^◇, 2^◇, …, 5^◇}张成得到

'={Ø , {t}, {u}, {t, u}, {s, u}, {s, u, v},

{s, t, u}, S₂}.

计算得技能背景(Q'₂, S₂, I')确定的知识结构为

K'={Ø , {3}, {4}, {1, 3, 4}, {4, 5}, {2, 4, 5},

{1, 3, 4, 5}, Q'₂},

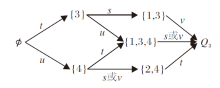
并得到技能背景(Q'₂, S₂, I')下技能集S₂的学习路径图, 如图4所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 (Q'2, S2, I')下S2的学习路径图Fig.4 Learning paths diagram for S2 in (Q'2, S2, I')

图4中有4条学习路径, 适合不同的学习者对技能集S₂中的技能进行有效学习.对∀ K∈ K, K≠ Q₂, 存在由K到其后继状态的有效技能.对于知识状态为{4}的学习者, 指导其学习有效技能s、t.若其知识状态变为{4, 5}或{1, 3, 4}, 说明其掌握技能s或t.若其知识状态变为{1, 3, 4, 5}, 说明其掌握技能s和t.若其知识状态未发生改变, 说明其未掌握技能s和t.

由此, 对于良好的技能背景, 得到学习路径图后, 可通过判断学习者的知识状态是否发生改变评估其是否掌握相应的有效技能.

设(Q, S, μ )是技能函数,

r= ∏q∈Q|μ (q) |.

当r> 1时, 技能函数(Q, S, μ )可分解为r个合取技能函数, 即r> 1时, 技能函数(Q, S, μ )可分解为r个技能背景.一个技能背景对应一种解决问题集Q的方法.

定义11 设(Q, S, μ )为技能函数,

r= ∏q∈Q|μ (q) |,

(Q, S, I_k)(k=1, 2, …, r)是由(Q, S, μ )分解得到的r个技能背景.

记

L(Q, S, μ )= ∪k=1, 2, …, rPL(Q, S, I_k),

L_K(Q, S, μ )={}( ∪i=1, 2, …, xK_i, T)|(K_i, T_i)∈ L(Q, S, μ ), T=T₁=…=T_x, 1≤ x≤ r}, LK_T(Q, S, μ )={(, ∩i=1, 2, …, yi)|Ki_, Ti₎∈ LK₍Q, S, μ ), K=K1₌…=Ky_, 1≤ y≤ r}

引理2 设(Q, S, μ )为技能函数, 对∀ (K, T)∈ L_K(Q, S, μ ), T通过技能函数μ 诱导得到的知识状态为K.记

K={K|(K, T)∈ L_K(Q, S, μ )},

则K为由技能函数μ 诱导得到的知识结构.

证明 设

r= ∏q∈Q|μ (q)|,

即存在r种解决问题集Q的方法.对∀ (K, T)∈ L_K(Q, S, μ ), 存在(K_i, T_i)∈ L(Q, S, μ ), i=1, 2, …, x, 使

T=T₁=…=T_x, K= ∪i=1, 2, …, xK_i.

当x=1时, 显然存在第k∈ {1, 2, …, r}种方法, 使得在此方法下用T能解决的问题集为K₁, 且在其它方法下用T能解决的问题集要么为Ø 要么为K₁.于是T通过技能函数μ 诱导得到的知识状态为 K=K₁.

当x> 1时, 存在x种方法, 使得在这x种方法下, 用T能解决的问题集分别为K₁, K₂, …, K_x, 且在其它方法下用T能解决的问题集要么为Ø , 要么K∈ {K₁, K₂, …, K_x}.于是T通过技能函数μ 诱导得到的知识状态为

K= ∪i=1, 2, …, xK_i.

综上所述, 对于(K, T)∈ L_K(Q, S, μ ), T通过技能函数μ 诱导得到的知识状态为K.记

K={K|(K, T)∈ L_K(Q, S, μ )},

显然Ø ∈ K, Q∈ K, 故K是由技能函数μ 诱导得到的知识结构.证毕.

定理7 设₁、₂为两个良级的集族, 且Ø ∈ ₁∪ ₂, 则T₁∪ ₂也是良级的.

证明 ₁、₂都是良级的, 说明对C∈ _i, L∈ _i, i=1, 2, 存在由C到L的紧路径.

对∀ C∈ ₁∪ ₂, L∈ ₁∪ ₂, 若C∈ ₁, L∈ ₁或C∈ ₂, L∈ ₂, 显然₁∪ ₂中存在由C到L的紧路径.不妨设C∈ ₁且L∈ ₂, 由Ø ∈ ₁∪ ₂可知₁∪ ₂中存在由C到Ø 的紧路径, 以及由Ø 到L的紧路径.于是₁∪ ₂中存在由C到L的紧路径.

综上所述, 对∀ C∈ ₁∪ ₂, L∈ ₁∪ ₂, ₁∪ ₂中存在由C到L的紧路径, 即₁∪ ₂是良级的. 证毕.

设(Q, S, μ )为技能函数,

r= ∏q∈Q|μ (q)|,

(Q, S, I_k)(k=1, 2, …, r)为由(Q, S, μ )分解得到的r个技能背景.分解得到的r个技能背景不一定都是正则的.本文只讨论分解得到的技能背景中至少有一个是正则的情形.记

_k={T|(K, T)∈ _PL(Q, S, I_k)}, T={T|K, T)∈ LK₍Q, S, μ )}.

显然由定义11可知,

T= ∪k=1, 2, …, rT_k, 且Ø ∈ T, S∈ T, 本文称(S, T)或直接称T是由技能函数(Q, S, μ )确定的能力结构.

推论5 设(Q, S, μ )为技能函数,

r= ∏q∈Q|μ (q)|,

(Q, S, I_k)(k=1, …, r)为由(Q, S, μ )分解得到的r个技能背景.若对于k=1, 2, …, r, _k是良级的, 则T是良级的.

定理8 设(Q, S, μ )为技能函数, (S, T)为由技能函数μ 确定的能力结构, T是良级的当且仅当μ 是良好的.

证明 设技能函数(Q, S, μ )诱导的知识结构为(Q, K).

⇒ .对于K∈ K, K≠ Q, K'是K的后继状态, 存在T∈ T, T'∈ T使得(K, T)∈ L_K(Q, S, μ ), (K', T')∈ L_K(Q, S, μ ), 且T⊂T', 则|T-T'|=1, 否则与T是良级的矛盾.即存在由K到K'的有效技能s∈ (T-T'), 因此μ 是良好的.

⇐.对于T∈ T, T'∈ T, 存在K∈ K, K'∈ K, 使得(K, T)∈ L_K(Q, S, μ ), (K', T')∈ L_K(Q, S, μ ).下面分两种情况进行讨论.

1)K, K'存在包含关系, 不妨设K⊂K'.

若K'是K的后继状态, 显然存在由T到T'的紧路径:T⊂T'.

若K'不是K的后继状态, 则存在K₁∈ K, K₂∈ K, …, K_x∈ K, x≥ 1, 使得

K=K₀⊂K₁⊂…⊂K_x⊂K_x+1=K',

且K_i是K_i-1(i=1, 2, …, x+1)的后继状态.存在T₁∈ T, T₂∈ T, …, T_x∈ T, x≥ 1, 使得

(K_i, T_i)∈ L_K(Q, S, μ ), i=1, 2, …, x.

显然存在由T到T'的紧路径:

T⊂T₁⊂…⊂T_x⊂T'.

2)K, K'不存在包含关系, 则存在

Ø =K₁, K₂, …, K_x∈ K, x≥ 1,

使得

Ø =K₁⊂…⊂K_x⊂K_x+1=K,

且K_i+1是K_i(i=1, 2, …, x)的后继状态.由1)可得由T到Ø 的紧路径T⊃…⊃Ø .同理可得由Ø 到T'的紧路径:Ø ⊂…⊂T'.因此存在由T到T'的紧路径.

综上所述, 对于T∈ T, T'∈ T, 存在由T到T'的紧路径, 即T是良级的. 证毕.

给定技能函数(Q, S, μ ),

T={T|(K, T)∈ L_K(Q, S, μ )}.

对于(K₁, T₁)∈ L_K(Q, S, μ ), (K₂, T₂)∈ L_K(Q, S, μ ), 若满足K₁⊂K₂, 且T₂是T中满足T₁⊂T₂的极小能力状态, 则K₂是知识状态K₁的后继状态.

推论6 设(Q, S, μ )为良好的技能函数, 对于(K₁, T₁)∈ L_K(Q, S, μ ), (K₂, T₂)∈ L_K(Q, S, μ ), 若K₂是K₁的后继状态, 则s∈ (T₂-T₁)是由K₁到K₂的有效技能.

定理9 设(Q, S, μ )为良好的技能函数.对∀ (K, T)∈ L_KT(Q, S, μ ), K≠ Q, 设K存在x(x≥ 1)个后继状态, 由K到其各个后继状态的有效技能的集合为D.若知识状态为K的学习者的能力状态为T_K, 则T⊆T_K, 且对∀ s∈ D, s∉T_K.

证明 设(S, T)是由(Q, S, μ )确定的能力结构.对∀ (K, T)∈ L_KT(Q, S, μ ), 存在T₁∈ T, T₂∈ T, …, T_y∈ T, y≥ 1, 使得(K, T₁)∈ L_K(Q, S, μ ), (K, T₂)∈ L_K(Q, S, μ ), …, (K, T_y)∈ L_K(Q, S, μ )且

T= ∩i=1, 2, …, yT_i.

显然, 知识状态为K的学习者至少掌握T中的所有技能, 即T⊆T_K.对∀ s∈ D, 若s∈ T_K, 则学习者的知识状态将达到K的某个后继状态, 矛盾.于是对∀ s∈ D, s∉T_K. 证毕.

特别地, 若学习者的知识状态为K=Q, 则存在T⊆S, 使得(Q, T)∈ L_KT(Q, S, μ ), 且该学习者至少掌握T中的所有技能.

例5 给定技能函数(Q₃, S₃, μ ), 其中

Q₃={1, 2, 3, 4}, S₃={s, t, u, v}, μ (1)={{s, t}, {t, u}}, μ (2)={{s, u}, {u, v}}, μ (3)={{t}}, μ (4)={{u}}.

显然

r= ∏q∈Q3|μ (q)|=4,

计算得

L(Q₃, S₃, μ )={(Ø , Ø ), (3, t), (4, u), (13, st), (24, su), (24, uv), (34, tu), (134, tu), (134, stu), (234, tuv), (Q3, s_tu), (Q3, t_uv), (Q3, S₃)}_, LK(Q3_, S3_, μ )₌{(Ø , Ø ), (3, t), (4, u), (13, st), (24, su), (24, uv), (134, tu), (Q3, stu)_, (Q3, tuv)_, (Q3, S3)}_, L_KT(Q3, S_3, μ )₌{(_Ø , Ø ), (3, t), (4, u), (13, st), (24, u), (134, tu), (Q3, tu)}.

显然, 由技能函数(Q₃, S₃, μ )确定的知识结构

K={Ø , {3}, {4}, {1, 3}, {2, 4}, {1, 3, 4}, Q₃}.

能力结构

T={Ø , {t}, {u}, {s, t}, {s, u}, {u, v}, {t, u},

{s, t, u}, {t, u, v}, S₃}.

显然, T是良级的, 即(Q₃, S₃, μ )是良好的.对∀ K∈ K, K≠ Q₃, 存在由K到其后继状态的有效技能.得到技能集S₃的学习路径图, 如图5所示.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 技能集S3的学习路径图Fig.5 Learning paths diagram for skill set S3

由图5可知, 技能s、v都是由知识状态{4}到{2, 4}的有效技能.知识状态为{4}的学习者通过学习技能s或技能v都能达到后继状态{2, 4}.另一方面, 根据定理9, 得到处于(Q₃, K)中任意知识状态的学习者对技能的掌握情况, 如表4所示, 表中知识状态为{1, 3}的学习者至少掌握技能s、t, 没有掌握技能v.

表4

Table 4

表4(Table 4)

表4 (Q3, K)中知识状态的技能掌握情况 Table 4 Skill mastery of knowledge state in (Q3, K) K\S3 s t u v Ø × × {3} × $\surd$ × {4} × × $\surd$ × {1, 3} $\surd$ $\surd$ × {2, 4} × $\surd$ {1, 3, 4} × $\surd$ $\surd$ × Q3 $\surd$ $\surd$

表4 (Q3, K)中知识状态的技能掌握情况 Table 4 Skill mastery of knowledge state in (Q3, K)

T是良级的说明对∀ K∈ K, K≠ Q, 存在由K到其后继状态的有效技能.换句话说, 知识状态为K的学习者通过学习一个技能便能改变原有的知识状态.此时, 不仅可指导学习者进行有效学习, 还能通过学习者对问题的回答情况评估其是否掌握相应的有效技能.若T不是良级的, 即存在k∈ {1, 2, …, r}, 使得_k不是良级的.本文考虑通过添加问题, 使得对于k=1, 2, …, r, _k是良级的.也就是说, 通过添加问题使新得到的技能函数是良好的.

设(Q, S, μ )为技能函数,

r= ∏q∈Q|μ (q)|,

(Q, S, I_k)(k=1, 2, …, r)是由(Q, S, μ )分解得到的r个技能背景.对∀ s∈ S, δ (s^k)(k=1, 2, …, r)表示T_k中包含技能s的极小集构成的集族.记

C={C∈ μ (q)|q∈ Q}

为技能函数(Q, S, μ )所有能力构成的集族.对于s∈ S, C_s⊆C表示C中含有技能s的能力构成的集族.

定理10 设(Q, S, μ )为技能函数,

r= ∏q∈Q|μ (q)|,

(Q, S, I_k)(k=1, 2, …, r)是由(Q, S, μ )分解得到的r个技能背景.若存在C∈ C, k∈ {1, 2, …, r}, s∈ S, t∈ S, 使得C∈ δ (s^k)且C∈ δ (t^k), 则添加满足如下两个条件的问题p, 不改变δ (s'^k), k=1, 2, …, r, s'∈ S, s'≠ s, s'≠ t, 且对于k=1, 2, …, r, 有C∉δ (s^k)或 C∉δ (t^k).

1)μ (p)={M}, 使得s∈ M⊆∩ C_s或t∈ M⊆

∩ C_t;

2)对∀ s'∈ M, s'≠ s, s'≠ t, k=1, 2, …, r, B∈ δ (s'^k), 有B⊂M.

证明 当C={s, t}时, 不妨设μ (p)={{t}}.显然问题p满足1)、2)条件, 且添加问题p之后不改变δ (s'^k), k=1, 2, …, r, s'∈ S, s'≠ s, s'≠ t.由{t}⊂C知{t}在r个技能背景中都是包含技能t的极小集, 且此时对于k=1, 2, …, r, 有C∉δ (t^k).

当C⊃{s, t}时, 取满足1)、2)条件的问题p, 且μ (p)={M}使得t∈ M⊆∩ C_t.由于对于k=1, 2, …, r, B∈ δ (s'^k), 有B⊂M, 因此新增问题p之后不改变δ (s'^k), k=1, 2, …, r, s'∈ S, s'≠ s, s'≠ t.显然M⊂C, 因此M在r个技能背景中都是包含技能t的极小集, 且此时对于k=1, 2, …, r, 有C∉δ (t^k).综上所述, 定理成立.证毕.

推论7 设(Q, S, μ )为技能函数,

r= ∏q∈Q|μ (q) |,

(Q, S, I_k)(k=1, 2, …, r)是由(Q, S, μ )分解得到的r个技能背景.若存在C∈ C, k∈ {1, 2, …, r}, s₁∈ S, s₂∈ S, …, s_m∈ S, 2≤ m≤ |S|, 使C∈ δ ( sik), i=1, 2, …, m, 则添加满足如下两个条件的m-1个问题p_j, j=1, 2, …, m-1, 不改变δ (s'^k), k=1, 2, …, r, s'∈ S, s'≠ s_i, i=1, 2, …, m, 且对于k=1, 2, …, r, 存在唯一的i∈ {1, 2, …, m}, 使得C∈ δ ( sik).

1)μ (p_j)={M}, 且存在唯一的i∈ {1, 2, …, m}, 使得s_i∈ M⊆∩ Csi;

2)对∀ s'∈ M, s'≠ s_i, i=1, 2, …, m, k=1, 2, …, r, B∈ δ (s'^k), 有B⊂M.

设(Q, S, μ )为技能函数, 其中

Q={q₁, q₂, …, q_n}, r= ∏q∈Q|μ (q) |.

(Q, S, I_k)(k=1, 2, …, r)是由(Q, S, μ )分解得到的r个技能背景.对于k∈ {1, 2, …, r}, q∈ Q, Cqk表示在第k个技能背景下分配给问题q的能力.以{ Cq1k, Cq2k, …, Cqnk}为矩阵的第k行, 得到r× n的矩阵B_{r× n}, 称B_{r× n}为技能函数(Q, S, μ )的方式矩阵.一个技能函数对应一个方式矩阵, 且方式矩阵的每行都表示解决问题集Q的一种方法, 即对应着一个技能背景.

给定技能函数(Q, S, μ ), 若μ 不是良好的, 根据定理10和推论7可通过添加问题使新得到的技能函数是良好的.下面给出获取良好技能函数及其方式矩阵的算法.

算法3 获取良好技能函数及其方式矩阵

输入 技能函数(Q, S, μ )

输出 良好的技能函数(Q', S, μ ')及其方式矩阵B

step 1 r= ∏q∈Q|μ (q) |, n=|Q|.

step 2 得到(Q, S, μ )的方式矩阵B_{r× n}, 对B_{r× n}的行进行重新排列, 使得第k种方法下的能力个数不少于第k+1种方法下的能力个数.

step 3 Q'← Q, k=1, 并执行如下操作:

WHILE k≤ r DO

对∀ s∈ S, 在B(k, :)中寻找δ (s^k);

对∀ C∈ B(k, :), 计算Ω (C)={s|C∈ δ (s^k)};

IF ∃C∈ B(k, :), |Ω (C) |> 1 THEN

记φ =φ '={Ω (C):C∈ B(k, :), |Ω (C) |> 1}, 其中φ (φ ')按Ω (C)的基数从大到小进行排列;

FOR i=2 to |φ '| DO

IF |φ '(i)- ∪j=1, 2, …, i-1(φ '(j)∩ φ '(i)) |≤ 1

THEN

φ (i)← Ø ;

ELSE

φ (i)← φ '(i)- ∪j=1, 2, …, i-1(φ '(j)∩ φ '(i));

END IF

END FOR

FOR i=1 to |φ | DO

α =|φ (i) |-1;

Q'← Q'∪ {q_|Q'|+1, q_|Q'|+2, …, q_|Q'|+α },

其中μ '(q_|Q'|+i)={M_|Q'|+i}, i=1, 2, …, α ,

满足推论7;

END FOR

对于i=1, 2, …, r, j=1, 2, …, α ,

B(i, |Q'|+j)← M_|Q'|+j;

END IF

k=k+1;

END WHILE

step 4 对∀ q∈ Q, μ '(q)=μ (q).

例6 给定技能函数(Q₄, S₄, μ ), 其中

Q₄={1, 2, 3}, S₄={a, b, c, d}, μ (1)={{b, d}}, μ (2)={{a, c}, {b, d}}, μ (3)={{a, b, c}, {b, d}}.

由

r= ∏q∈Q4|μ (q) |=4, |Q₄|=3

可得与技能函数(Q₄, S₄, μ )对应的方式矩阵为

B_{4× 3}= {b, d}{a, c}{a, b, c}{b, d}{a, c}{b, d}{b, d}{b, d}{a, b, c}{b, d}{b, d}{b, d}.

B_{4× 3}的每行都对应一个技能背景.当k=1时, 在{{b, d}, {a, c}, {a, b, c}}中寻找包含任意技能s∈ S₄的极小集, 可得到带↙的技能背景(Q₄, S₄, I₁), 如表5所示.由表可知,

δ (a¹)=δ (c¹)={a, c}, δ (b¹)=δ (d¹)={b, d}.

表5

Table 5

表5(Table 5)

表5 带↙的技能背景(Q4, S4, I1) Table 5 Skill context (Q4, S4, I1) with ↙ a b c d 1* ={b, d} 0 ↙ 0 ↙ 2* ={a, c} ↙ 0 ↙ 0 3* ={a, b, c} 1 ↙ 1 0

表5 带↙的技能背景(Q4, S4, I1) Table 5 Skill context (Q4, S4, I1) with ↙

显然, 技能函数(Q₄, S₄, μ )不是良好的.根据定理10, 添加2个问题:

μ '(4)={{b}}, μ '(5)={{a}},

得到良好的技能函数(Q'₄, S₄, μ '), 其中

Q'₄=Q₄∪ {4, 5},

且对∀ q∈ Q₄, μ '(q)=μ (q).

给定一个技能函数(Q, S, μ ), 运用算法3判断其是否是良好的并输出一个良好的技能函数及其方式矩阵.基于良好的技能函数, 下面给出寻找技能集的学习路径的算法.

算法4 基于良好技能函数, 获取学习路径

输入 良好技能函数(Q, S, μ )对应的方式矩阵

输出 技能集S的学习路径图

step 1 给定一个空图G, T← Ø , K← Ø .

step 2 ∂ ← Ø , ρ ← Ø , 其中∂ 表示G中所有边的集合, ρ 表示G中的所有学习路径.

step 3 对于k=1, 2, …, r, B(k, :)张成_k.

step 4 T= ∪k=1, 2, …, rT_k, T按集合的包含关系由小到大进行排列.

step 5 对于i=1, 2, …, |T|,

K(i)← {q∈ Q|∃C∈ μ (q), C⊆T(i)}.

step 6 对于i=1, 2, …, |K|-1, j∈ {1, 2, …, |K|}, 执行如下操作:

IF K(j)是K(i)的后继状态 THEN

∂ ← ∂ ∪ (K(i), K(j)), 其中(K(i), K(j))是由K(i)指向K(j)的边, 边的标记为T(j)-T(i);

END IF

step 7 根据∂ 找出所有学习路径ρ , 画出学习路径图G.

例7 续例6, 良好技能函数(Q'₄, S₄, μ ')对应的方式矩阵为

B_{4× 5}= {b, d}{a, c}{a, b, c}{b}{a}{b, d}{a, c}{b, d}{b}{a}{b, d}{b, d}{a, b, c}{b}{a}{b, d}{b, d}{b, d}{b}{a}.

经过计算得技能函数(Q'₄, S₄, μ ')确定的良级能力结构为

T={Ø , {a}, {b}, {a, b}, {a, c}, {b, d}, {a, b, c},

{a, b, d}, S₄},

对应的知识结构

K={Ø , {5}, {4}, {4, 5}, {2, 5}, {1, 2, 3, 4},

{2, 3, 4, 5}, Q'₄}.

画出技能集S₄的学习路径图, 如图6所示.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 技能集S4的学习路径图Fig.6 Learning paths diagram for skill set S4

图6中{4, 5}$→ ^a${2, 3, 4, 5}表示知识状态为{4, 5}的学习者通过学习并掌握技能c可达到状态{2, 3, 4, 5}.若学习者没有达到状态{2, 3, 4, 5}, 说明没有掌握技能c.

当技能函数是良好的, 根据技能集的学习路径图不仅可有效指导学习者学习, 还可根据学习者对问题的回答情况评估其是否掌握相应的有效技能.

合取技能函数与析取技能函数均为一般技能函数的特殊情形.合取技能函数针对一题一解.析取技能函数和一般的技能函数针对一题多解.本文着重考虑合取技能函数与一般技能函数满足良好性并寻找学习路径的方法, 而对于析取技能函数, 讨论方法与一般的技能函数类似, 本文将不再赘述.

实验数据集是2个来自UCI数据库的数据集, 分别为COVID-19 Surveillance数据集和StoneFlakes数据集.根据本文讨论的问题, 对数据进行离散化处理, 得到2个新的数据集, 分别表示为技能背景(Q₅, S₅, I)和技能函数(Q₆, S₆, μ ), 具体如表6和表7所示, 其中

Q₅={1, 2, …, 14}, S₅={a, b, c, d, e, f, g}, Q6₌{1, 2, …, 10}, S6₌{h, i, j, k, l, m, n}.

表6

Table 6

表6(Table 6)

表6 技能背景(Q5, S5, I) Table 6 Skill context (Q5, S5, I) Q5\S5 a b c d e f g 1 1 1 1 1 1 0 0 2 1 1 0 1 1 0 0 3 1 1 1 1 0 1 0 4 1 1 0 1 0 1 0 5 1 0 0 0 0 0 1 6 1 1 1 0 0 0 1 7 1 1 0 0 0 0 1 8 1 1 1 1 0 0 0 9 1 0 0 1 1 0 0 10 0 1 0 1 1 0 0 11 1 0 0 1 0 1 0 12 0 1 0 1 0 1 0 13 0 1 0 0 0 0 1 14 0 0 0 0 0 0 1

表6 技能背景(Q5, S5, I) Table 6 Skill context (Q5, S5, I)

表7

Table 7

表7(Table 7)

表7 技能函数(Q6, S6, μ ) Table 7 Skill function(Q6, S6, μ ) q∈ Q6 C∈ μ (q) q∈ Q6 C∈ μ (q) 1 {k}, {l, m, n} 6 {i, j, k} 2 {j}, {k, m} 7 {h, j}, {h, l, m, n} 3 {j, k}, {j, l} 8 {h, j} 4 {i, l}, {i, m, n} 9 {h, j, l} 5 {i, l}, {i, j, m, n} 10 {h, i, k, l}, {h, l, m, n}

表7 技能函数(Q6, S6, μ ) Table 7 Skill function(Q6, S6, μ )

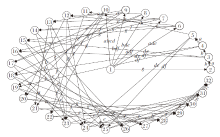
根据实验分析可知技能背景(Q₅, S₅, I)不满足良好性.由算法2得到在技能背景(Q₅, S₅, I)下技能集S₅的学习路径图, 如图7所示.在学习路径图中, 顶点表示知识状态, 用阿拉伯数字表示知识状态的序号.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 (Q5, S5, I)下S5的学习路径图Fig.7 Learning paths diagram for S5 in (Q5, S5, I)

由图7可发现, 并不是每条边上都只有一个技能, 这造成无法评估学习者是否掌握相应技能的情形.在图7中, 知识状态序号为1的学习者通过学习技能abcd后达到序号为10的知识状态, 说明其掌握技能abcd.如果知识状态未发生改变, 则无法判断其是否掌握技能abcd.事实上, 该学习者可能已掌握abcd中的某些技能, 因此有必要进一步优化技能背景(Q₅, S₅, I).

运用算法1对技能背景(Q₅, S₅, I)添加问题15、16、17, 得到满足良好性的技能背景(Q'₅, S₅, I'), 如表8所示.

表8

Table 8

表8(Table 8)

表8 良好的技能背景(Q'5, S5, I') Table 8 Well-formed skill function(Q'5, S5, I') Q'5\S5 a b c d e f g 1 1 1 1 1 1 0 0 2 1 1 0 1 1 0 0 ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ 15 1 0 0 0 0 0 0 16 0 1 0 0 0 0 0 17 0 0 0 1 0 0 0

表8 良好的技能背景(Q'5, S5, I') Table 8 Well-formed skill function(Q'5, S5, I')

通过添加问题得到的技能背景(Q'₅, S₅, I')是良好的, 即技能背景(Q'₅, S₅, I')确定的能力结构是良级的.此时, 技能集S₅的学习路径图如图8所示.

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 (Q'5, S5, I')下S5的学习路径图Fig.8 Learning paths diagram for S5 in (Q'5, S5, I')

图8中处于任意知识状态的学习者都可通过学习一个有效技能改变自己原本的知识状态.此时, 不仅可通过学习路径图指导学习者进行有效学习, 还可通过判断学习者的知识状态是否发生改变评估其是否掌握相应的有效技能.

在解决问题集Q的方法只有一种的情形下, 在技能背景下寻找每步只需学习一个有效技能的学习路径图.一般地, 解决问题集Q的方法可能不止一种.

对于技能函数(Q₆, S₆, μ ),

r= ∏q∈Q6|μ (q) |=128,

由算法3获得满足良好性的技能函数(Q'₆, S₆, μ ')及其方式矩阵, 其中

Q'₆=Q₆∪ {11, 12, …, 16}.

对

∀ q∈ Q₆, μ '(q)=μ (q),

且

μ '(11)={{h}}, μ '(12)={{l}}, μ '(13)={{m}}, μ '(14)={{n}}, μ '(15)={{j}}, μ '(16)={{i, j}}.

运用算法4可获得在技能函数(Q'₆, S₆, μ ')下技能集S₆的逐步学习路径图.对于每步只需学习一个有效技能的学习路径图, 不仅可有效指导学习者进行学习, 还可根据学习者知识状态的变化评估其是否掌握相应的有效技能, 由此说明算法的有效性.

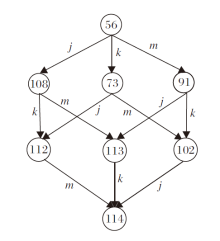
技能函数(Q'₆, S₆, μ ')下技能集S₆的部分学习路径如图9所示.由图可知, 序号为56的知识状态到其后继状态的有效技能集D={j, k, m}, 可指导状态为序号56的学习者对技能j、k、m进行有效学习.若该学习者的知识状态序号达到108, 说明其掌握技能j; 若其知识状态序号达到91, 说明其掌握技能m; 若其知识状态序号达到73, 说明其掌握技能k.另一方面, 若学习者的知识状未发生改变, 则说明其未掌握技能j、k、m.

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 技能集S6的部分有效学习路径图Fig.9 Partial effective learning paths diagram for skill set S6