在单智能体强化学习领域, Tang等^[5]对访问过的状态计数, 访问次数越少则奖励越多, 刺激智能体更多地探索访问次数较少的状态.Pathak等^[11]将预测的下一步状态和实际的下一步状态之差作为智能体的好奇心, 并作为智能体的内在奖励, 使其在稀疏奖励的环境下也能帮助智能体学习.Houthooft等^[12]将智能体经过状态转移后新的动态模型和原有动态模型的KL散度视为信息增益, 并作为内在奖励信号.Sequeira等^[13]提出4个评估维度(新颖性、动机、控制力、效价), 用于评估智能体与环境的关系, 将其转化为数值特征, 用于综合衡量智能体的内在奖励, 大幅加速智能体的训练效率.

相比单智能体强化学习领域的成功, 多智能体强化学习的发展相对较弱.Hughes等^[14]利用智能体厌恶不平等奖赏的特性, 帮助智能体解决社会困境.Sequeira等^[15]定义智能体通过内在动机机制学习获得社会意识的行为, 这种行为可在智能体获得社会认可的过程中进行权衡, 从而使整个群体表现更成功.

传统基于值函数的算法在单智能体中都有着较好的运用, 但在多智能体环境中, 由于环境的不稳定, 传统的单智能体算法无法有效发挥作用, 需要专门的多智能体算法解决该类问题.

多智能体算法多基于演员-评论家(Actor-Critic, AC)的框架, 针对每个智能体训练一个Actor网路和Critic网络.每个Actor网络根据当前智能体观察到的局部信息 otN选择动作 atN, 负责智能体的行为决策.每个Critic可通过所有Actor获得全局信息以计算Q值, 作为对当前Actor动作的反馈, 并对该行为进行效用评估.

MADDPG同样基于多智能体AC框架.算法针对每个智能体i的累计期望奖励为

$J\left(\theta_{i}\right)=E_{s \sim \rho^{\pi}, a_{i} \sim \pi_{\theta_{i}}}\left[\sum_{t=0}^{\infty} \gamma^{t} r_{i, t}\right]$

其中,

θ =[θ ₁, θ ₂, …, θ _n],

表示第i个智能体策略的参数,

π =[π ₁, π ₂, …, π _n],

表示第i个智能体的策略, s为智能体的全局观测状态.集中式的Critic更新方法借鉴时序差分(Temporal Difference, TD)学习的思想, 即

$L\left(\theta_{i}\right)=E_{s, a, r, s^{\prime}}\left[\left(y-Q_{i}\left(s, a_{1}, a_{2}, \cdots, a_{n}\right)\right)^{2}\right]$,

其中,

y=r_i+γ Q'_i(s', a'₁, a'₂, …, a'_n),

Q'_i表示目标网络, 此时可采用拟合逼近得到其它智能体的策略, 而不需要通信交互.由于每个智能体独立学习自己的Q函数, 使不同的智能体可有不同的奖励函数.

心理学家认为, 为推动智能体进行探索, 不应只有环境给予的外在动机, 还应有智能体自身蕴含的内在动机.外在动机表示智能体希望获得外部环境赐予的外部奖励.而内在动机来自于智能体内部, 并不是为了获得环境分配的奖励, 而是为了获得内在的满足感, 同时也并不因外在环境的变化而变化.

同样, 研究人员试图在强化学习中引入内在动机的元素.Singh等^[16]提出内在动机强化学习模型(Intrinsic Motivation Reinforcement Learning, IMR-L), 将环境分解为内部环境和外部环境.外部环境表示智能体外部的场景, 内部环境存在于智能体内部.奖励也相对应地分解为内部奖励和外部奖励.智能体的最终奖励为内部奖励和外部奖励之和.

在构建考虑强化学习框架时, 情感作为一种自然的智能体内在属性, 同样被研究人员考虑作为内在动机引入强化学习中.最初定义智能体的情感为强化学习中的值函数或奖励函数.然而, 由于智能体情感的连续性和动态性, 衡量标准不应只着眼于当前状态, 而应同时考虑当前状态和未来的状态.时序差分恰好可以解决这一问题, 其由奖励和下一状态的预期V值得到, 此时智能体情感的衡量不仅基于当前状态的奖励, 还基于智能体对下一状态的预测.

由此, Broekens等^[17]试图将智能体的情感与强化学习中的时序差分相联系, 情感和时序差分的产生诱因、功能和目的都是相似的, 并由此提出基于时序差分的情感理论, 提出智能体正(负)时序差分信号分别为快乐(痛苦)的体现.然而文献[17]只是提出理论, 并未明确指出情感在智能体的训练过程中是如何促进智能体的学习, 也并没有实际的应用场景, 缺乏实验依据.

本文构建一个2维的情感空间, 情感变量E_t= [e1, e2]T, 其中, e₁∈ [0, 1], e₂∈ [0, 1].E_t为智能体的复合情感, e₁、e₂分别表示兴奋和愤怒对应的情感强度值, 而智能体的复合情感为这二维的情感强度值的综合体现.各情感强度值不同, 表现的复合情感也不同, 情感值表示为智能体对任务目标不同的情感倾向.

为了解决稀疏奖励问题, 本文使用基于时序差分的情感理论作为智能体情感的衡量标准, 时序差分

TD=r+γ maxa'Q(s', a')-Q(s, a).

与单纯将奖励或值函数作为衡量智能体的标准不同, 时序差分关注智能体两个连续状态, 使其情感的判断并不单单关注于当前状态的奖励和值函数, 而是关注当前和未来的智能体的奖励和值函数的变化值, 使智能体的情感具有连续性和动态性, 也大幅增强衡量的准确性.每个智能体由于其从环境中获得的TD值不同, 智能体的情感值也不相同.根据TD值正负的不同, 为智能体的情感变量赋予不同的初值.本文称为情感衍生模块.

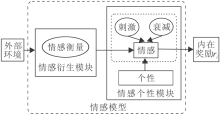
在多智能体环境下, 由于每个智能体都有固有个性, 因个性不同, 智能体对于同一事件的反应和思维方式也不同, 对智能体的行为和心理的倾向都有所影响.相比同类型的智能体, 不同个性的智能体体现多智能体环境中智能体的异构性和多样性.智能体情感模型框图如图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 智能体情感模型框图Fig.1 Framework of agent emotion model

本文利用人格五因素模型(Openness Conscien-tiousness Extraversion Agreeableness Neuroticism, OCEAN)描述每个智能体的个性向量^[18].OCEAN可描述性格的5个广泛的维度, 考虑的5个主要因素是开放性、尽责性、外向性、可同意性、神经质, 用向量表示为

P=[p₀, p₁, p₂, p₃, p₄].

个性向量中每个要素取值在[-1, 1]内, 值越大表示智能体个性中该要素越强.在训练过程中, 智能体的个性值不会发生改变.

在智能体的训练过程中, 智能体的情感将发生变化, 主要原因是内在的情感衰减和外在的情感刺激.情感衰减表示智能体的情感会随时间的推移而慢慢减弱.情感刺激表示也会因为受外界的刺激而发生改变.这两个变化均会受到智能体个性的影响.

心理学中情感强度第三定律指出, 情感强度与持续时间成负指数函数关系:

φ (E_t)=E₀e^-t,

此处E₀表示智能体初始情感值, t为持续时间.由于智能体的衰减速率与智能体的个性密切相关, 性格会对情感的波动产生影响, 内向的人情感比外向的人更容易波动^[19].因此个性悲观的智能体会比个性积极的智能体衰减速率更快, 情感衰减公式可表示为

φ (E_t)=KE₀e^-t,

其中, K为常数, 大小由智能体的个性决定.K由常数矩阵X和性格向量P决定,

K=exp(XP)= exp([x0_, x1_, x2_, x3_, x4_][p0_, p1_, p2_, p3_, p4_]T⁾,

此处

$\sum_{i=0}^{4} x_{i}=1$,

x_i为OCEAN的第i个人格因素对情感的影响系数.

外界的刺激同样影响智能体的情感变化.根据前期研究^[20], 本文使用隐马尔可夫模型(Hidden Mark-

ov Model, HMM)求得情感转移后的概率分布, 即定义一个五元组:

M=(E, S, π , A, B),

其中, E表示情感, S表示刺激, π 表示情绪状态的分布, 由个性P计算得到, A表示情感状态转移矩阵, B表示刺激矩阵.

ω (E_t)=HMM((P, E_t-1, S)).

在衰减和刺激后得到智能体在当前t时刻的情感, 即

E_t=φ (E_t-1)+ω (E_t-1),

本文将该部分称为情感个性模块.

对比情感模型中E_t的二维情感分量的值:当此时E_t位于情感空间对角线以下时, 给予智能体正的内在奖励; 当此时E_t位于情感空间对角线以上时, 给予智能体负的内在奖励.

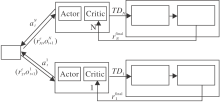
基于情感的异构多智能体激励机制, 本文提出MEADDPG.在MADDPG的基础上, 算法将情感模型看作智能体的内在环境, 在内在动机理论的指导下, 生成的内在奖励与环境给予的外在奖励一起组成智能体的最终奖励, 存入经验池中, 用于指导智能体策略的优化.MEADDPG框图如图2所示.算法步骤如算法1所示.

算法 1 MEADDPG

for episode = 1 to M do

初始化随机过程N, 进行动作探索, 得到初始状态s

for t = 1 to max-episode-length do

对每个智能体i, 关于当前策略选择动作

a_i = uθi(s_i) + N_t

执行动作a=(a₁, a₂, …, a_N), 得到外部奖励r_e

和新状态s'

TD_i=r_e+γ maxa'Q(s'_i, a'_i)-Q(s_i, a_i)

设置E_t=φ (E_t-1)+ω (E_t-1)

得到内在奖励r_i

r=r_i+r_e

在经验池 D中存储(s, a, r, s')

s ← s'

for agent i = 1 to N do

从经验池 D中随机采样

更新actor和critic

end for

更新目标网络参数

end for

end for

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 基于情感的多智能体决策分析Fig.2 Multi agent decision analysis based on emotion

由于每个智能体独立学习自己的Q函数, 使每个智能体可有独立的奖励函数.智能体在t时刻的最终奖励为内在奖励与外在奖励之和:

rfinalt= rte+ rti.

进一步定义智能体的折扣奖励:

Rfinalt= ∑l=0∞γ ^l( rt+le+ rt+li).

此时算法针对每个智能体i的累计期望奖励为

$J\left(\theta_{i}\right)=E_{s \sim \rho, a_{i} \sim \pi_{\theta_{i}}}\left(\sum_{t=0}^{\infty} \gamma^{t} r_{i, t}^{\text {final }}\right)$

针对每个智能体, 状态值函数更新方程为

$L\left(\theta_{i}\right)= \quad E_{s, a, r, s^{\prime}}\left[\left(R_{t}^{\text {final }}+\gamma Q_{i}^{\prime}\left(s^{\prime}, a_{1}^{\prime}, a_{2}^{\prime}, \cdots, a_{n}^{\prime}\right)-Q_{i}\right)^{2}\right] .$

本文以多智能体追逃任务为仿真实验场景.任务场景具体描述如下:在一个二维平面上, 有m个逃跑者(任务目标)和n个追捕者(研究主体), 所有智能体可出现在任意坐标上, 并向任意方向移动.智能体移动步长为实验预设值, 设置追捕者和逃跑者的移动步长均为0.1, 即在每个时间步追捕者和逃跑者均移动0.1的距离.逃跑者的逃跑方向随机.所有追捕者默认组成一个追捕团队以追捕逃跑者.智能体的捕获半径为0.08, 当有一个追捕者与逃跑者的距离小于0.08时视为捕获成功.捕获成功后的追捕者可继续追捕其他逃跑者, 直到所有逃跑者被捕获为止.追捕者须在200步内追到逃跑者, 此时视为任务成功; 若追捕者未在200步内追到逃跑者, 视为任务失败.

实验环境如图3所示.A₁、A₂、A₃为追捕者, B₁为逃跑者, 圆圈为该追捕者的视野范围, 视野范围的数值可控.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 实验环境Fig.3 Experiment environment

实验算法学习率为0.001, 批次大小为64, 迭代次数为5 000.

对比方法如下.1)MADDPG^[3].2)独立深度确定性策略梯度算法(Independent Deep Deterministic Policy Gradient, IDDPG)^[21].基于确定性策略, Critic只能根据当前Actor的局部信息计算当前Q值.3)独立情感深度确定性策略梯度算法(Emotion-Based Independent Deep Deterministic Policy Gradient, IED-DPG).基于IDDPG并利用本文的基于情感的异构多智能体激励机制.4)内在好奇心模块算法(In-trinsic Curiosity Module, ICM)^[12].利用智能体的预测误差激励智能体探索.

本文共设计3组实验, 分别从目标数量和视野范围的角度对实验环境的奖励稀疏级别进行分级, 一级最低, 三级最高, 如表1所示.

表1

Table 1

表1(Table 1)

表1 实验环境稀疏级别 Table 1 Sparse levels of experimental environments 目标数量 视野范围 稀疏级别 实验一 单目标 全局 一级 实验二 多目标 全局 二级 实验三 单目标 局部 三级

表1 实验环境稀疏级别 Table 1 Sparse levels of experimental environments

在实验中, 设置追捕者数量为3, 逃跑者数量为1, 即设定一个3追1的单目标追逃场景.在每个时间步, 智能体都能观察自身和队友在环境中的位置及逃跑者的位置, 即智能体当前视野为全局视野.在稀疏级别为一级时, 只有最终追到逃跑者时追捕者奖励+5, 其余情况奖励均为0.各方法的实验结果如图4所示.

由图4可看出, 随着迭代次数的增加, 成功率不断上升, 所需时间步逐渐减小, 智能体已逐渐学习到追捕策略.而情感的加入会使智能体直观地感受到自身每步行动的优劣, 从而通过为其增加内在奖励的方式, 帮助智能体调整追捕方针, 更快更好地学习到最优的策略.

当迭代次数达到2 000时, MEADDPG和IEDDPG的成功率已基本趋于稳定, 成功追捕所需的步长也越来越短.当迭代次数达到5 000时, MEADDPG的成功率已基本稳定在0.9左右, 时间步稳定在25步左右.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 3追1全视野场景下各方法实验结果对比Fig.4 Experimental result comparison of 3 pursuers pursuing 1 evader by different methods in a full field scene

相比单纯的多智能体算法(MADDPG、IDDPG), 本文方法在成功率和时间步上都有大幅提升.相比单纯的多智能体算法, ICM在此环境下对智能体的训练有一定的促进作用, 但结果仍略逊于MEADD-PG.由此可看出, 在稀疏奖励的环境下, MEADDPG对智能体训练确实具有一定的促进作用.

有无情感内在奖励下的智能体的追捕情况如图5所示, 追捕者为圆圈, 逃跑者为方块.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 有无情感内在奖励时智能体的追捕情况Fig.5 Pursuit situation of agent with and without emotional intrinsic reward

图5(a)中3个追捕者利用MEADDPG进行训练, 3个追捕者都学习到良好的追捕策略, 对逃跑者形成围捕之势, 在22步时追到智能体.(b)中3个追捕者利用MADDPG训练, 智能体学习的追捕策略明显劣于(a)中的智能体, 由于缺乏奖励而导致训练的不足, 不是所有的智能体都学会如何追捕智能体, 更未学会如何与他人合作完成任务.

本次实验在目标数量上加大难度.设置追捕者数量为4, 逃跑者数量为2, 即设定一个4追2的多目标追逃场景.智能体当前视野为全局视野.在稀疏级别为二级时, 只有两位逃跑者都被追到时, 才视为成功, 此时奖励+5, 其余情况奖励均为0.

相比单目标实验, 此时智能体需要捕获2个逃跑者后任务才会判定成功, 智能体数量的增加也使神经网络需要处理的信息数量增多, 增加网络负担.这些都导致智能体获得外在奖励变得更困难, 奖励环境更稀疏, 智能体的训练难度更大.

各方法在此场景下的实验结果如图6所示.由图6可看出, 由于实验难度的加大, 4种方法的成功率有所下降, 需要的时间步数有所增加, 但MEAD- DPG和IEDDPG的提升效果依旧十分明显.当迭代次数达到5 000时, MEADDPG和IEDDPG的成功率基本维持在0.8左右, MEADDPG时间步基本维持在50步左右, 此时IDDPG已基本失效.由于目标的数量增多, ICM对训练效果的提升逐渐降低.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 4追2全视野场景下各方法实验结果对比Fig.6 Experimental result comparison of 4 pursuers pursuing 2 evaders by different methods in a full field scene

由此可见, 在多目标的追捕环境下, 相比单目标状况虽然奖励更稀疏, 难度更大, 但MEADDPG依然具有有效性和适应性.

本次实验在视野范围方面加大难度.基于3追1的单目标追逃场景, 在每个时间步, 智能体只能观察到以自身为圆心、5个步长为半径的圆内的追捕者或逃跑者, 即智能体当前视野为局部视野.智能体的奖励设置与单目标追逃场景相同.视野范围的缩小使智能体通过观察得到的信息大幅减少, 进而导致智能体训练不足, 无法在规定步数内完成任务, 获得外部奖励的难度加大, 此时稀疏级别为三级.

各方法在此场景下的实验结果如图7所示.由图可看出, 由于智能体视野的缩小, 智能体存在无法观察到目标的情况, 虽然相比全局视野, MEADD-PG、IEDDPG成功率有所下降, 但相比MADDPG、ID-DPG, MEADDPG和IEDDPG提升效果依然较大, 而此时ICM与MADDPG效果类似, 说明此时对于智能体的促进作用已基本消失.这些结果均反映MEADDPG在智能体视野受限的环境下效果依然较优, 不会因为实验环境的改变而改变, 具有较好的鲁棒性.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 3追1局部视野场景下各方法实验结果对比Fig.7 Experimental result comparison of 3 pursuers pursuing 1 evader by different methods in a partial field scene