引用本文
张晓彤, 王嘉诚, 何景涛, 陈仕韬, 郑南宁. 面向不确定性环境的自动驾驶运动规划:机遇与挑战. 模式识别与人工智能, 2023,36(1): 1-21
ZHANG Xiaotong, WANG Jiacheng, HE Jingtao, CHEN Shitao, ZHENG Nanning. Motion Planning under Uncertainty for Autonomous Driving:Opportunities and Challenges. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(1): 1-21.  
Doi: 10.16451/j.cnki.issn1003-6059.202301001
Permissions
Copyright©2023, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
面向不确定性环境的自动驾驶运动规划:机遇与挑战
张晓彤1, 王嘉诚1, 何景涛1, 陈仕韬1, 郑南宁1
1.西安交通大学 人工智能与机器人研究所 西安 710049
通讯作者:

郑南宁,博士,教授,主要研究方向为计算机视觉、模式识别.E-mail:nnzheng@mail.xjtu.edu.cn.

作者简介:

张晓彤,硕士研究生,主要研究方向为自动驾驶车辆的运动规划.E-mail:zxt19991118@stu.xjtu.edu.cn.

王嘉诚,硕士研究生,主要研究方向为无人驾驶车辆的路径规划.E-mail:294022042@qq.com.

何景涛,硕士研究生,主要研究方向为基于强化学习的自主导航.E-mail:

陈仕韬,博士,助教,主要研究方向为无人驾驶. E-mail:chenshitao@mail.xjtu.edu.cn.

收稿日期: 2022-12-20 接受日期: 2023-01-28
摘要

运动规划算法作为自动驾驶系统中的重要研究内容,愈发受到研究者们关注.然而目前多数算法仅考虑在确定性结构化环境中的应用,忽视动态交通环境中潜在的不确定性因素.文中面向不确定性环境,将运动规划算法总结为两类:部分可观测马尔可夫决策过程(POMDP)和概率占用栅格图(POGM),从理论基础、求解算法、实际应用三方面进行介绍.基于当前置信状态,POMDP计算使未来折扣奖励最大的策略.POGM使用概率表征对应栅格上的占用情况,衡量车流动态变化的可能性,良好表征不确定性情况.最后,总结不确定性环境中当前运动规划问题面临的主要挑战和未来可能的研究方向.

关键词: 自动驾驶; 运动规划; 部分可观测马尔可夫决策过程(POMDP); 概率占用栅格图(POGM)
中图分类号:TP181
Motion Planning under Uncertainty for Autonomous Driving:Opportunities and Challenges
ZHANG Xiaotong1, WANG Jiacheng1, HE Jingtao1, CHEN Shitao1, ZHENG Nanning1
1. Institute of Artificial Intelligence and Robotics, Xi'an Jiaotong University, Xi'an 710049
Corresponding author：
ZHENG Nanning, Ph.D., professor. His research interests include computer vision and pattern recognition.

About Author:
ZHANG Xiaotong, master student. Her research interests include motion planning for autonomous vehicles.
WANG Jiacheng, master student. His research interests include path planning for autonomous vehicles.
HE Jingtao, master student. His research interests include autonomous navigation based on reinforcement learning.
CHEN Shitao, Ph.D., assistant professor. His research interests include driveless vehicles.

Abstract

Motion planning algorithm, as an important part of autonomous driving systems, draws increasing attention from researchers. However, most existing motion planning algorithms only consider their application in deterministic structured environments, neglecting potential uncertainties in dynamic traffic environments. In this paper, motion planning algorithms are divided into two categories for the uncertain environment: partially observable Markov decision process and probability occupancy grid map.The two categories are introduced for three aspects: theoretical foundation, solution algorithm and practical application. The strategy with the maximum discounted reward in the future is calculated by partially observable Markov decision process based on the current confidence state. Probability occupancy grid map utilizes probability to represent the occupancy status of corresponding grids, measuring the possibility of dynamic changes in traffic flow, and well representing the uncertainty. Finally, the main challenges and future research directions for motion planning in uncertain environments are summarized .

Key words: Autonomous Driving; Motion Planning; Partially Observable Markov Decision Process(POMDP); Probability Occupancy Grid Map(POGM)

自动驾驶系统是指一种可在部分或完全脱离人类驾驶员的情况下实现车辆安全行驶的自主系统, 主要包括环境感知、路径规划、行为决策、导航控制等主要技术模块[1].车辆使用多种车载传感器获取车辆自身状态和所处环境信息, 并基于传感器技术、信号处理技术、通讯技术、自动控制技术、计算机技术、人工智能技术等多领域技术对数据做出分析和判断, 最终依据环境和自身意图完成类人的自主决策控制.

由于自动驾驶和辅助驾驶技术不断发展和进步, 汽车工业正迎来一次智能化浪潮.以车道偏离预警、车道保持、全速域自适应巡航等为代表的一系列辅助驾驶功能, 在乘用车上逐渐普及, 并被越来越多的消费者接受.以辅助驾驶技术为主的渐进式自动驾驶路线开始与变革式的完全自动驾驶路线在人工智能赛道上出现交汇[2].得益于传感器、通信等相关技术的进步, 自动驾驶领域迎来快速发展的机遇, 汽车的智能化应用也在部分场景展现出更多的可能性.现阶段自动驾驶技术大规模应用的主要阻碍是“ 不确定性” 挑战, 特别是动态交通环境带来的不确定性几乎会影响到相关算法的每个阶段.

路径规划算法作为衔接多个技术模块的重要环节, 存在的不确定性问题尤为突出.然而目前大部分自动驾驶运动规划的研究工作依然基于确定性假设, 难以处理更动态的不确定性环境.确定性规划虽然有精密的物理模型和动力学模型为其提供良好的先验知识, 但通常仅适用于特定、动态程度较低的场景, 在复杂场景下缺乏实际应用的意义.自动驾驶车辆在复杂拥堵的交通场景下, 需要有效地与交通流交互, 这要求主体车辆必须预测自身行为对其它车辆行为的影响, 得到在未来一段时间内安全的轨迹, 即进行具有交互性与预测性的规划.车辆之间的相互作用是一种复杂和耦合的动态交通状况, 局部偏差会在车辆间进行传播, 极易导致不确定性的快速积累[3].其他交通参与者行为具备灵活性和随机性, 并有一定的集体特性, 目前对其轨迹预测的可靠性仍有待提升.

自动驾驶汽车需要具备更通用性的方法建模交通环境, 并实时响应难以预测的状况, 从而保证即使在复杂的城市情况下, 车辆也能做出及时、安全的响应.不完整的环境表示和不确定性会影响运动规划, 因此仍有两个因素需要进一步深入研究:不确定性环境的表征和该环境下的规划.本文将不确定性下的自动驾驶运动规划算法归纳为两类.1)部分可观测马尔可夫决策过程(Partially Observable Markov Decision Process, POMDP), 基于当前置信状态, 计算使未来折扣奖励最大的策略, 在车道变更、路口车流、行人交互场景内均有良好应用.2)概率占用栅格图(Probability Occupancy Grid Map, POGM), 使用概率表征对应栅格上的占用情况, 衡量车流动态变化的可能性, 良好表征不确定性情况.本文从问题建模、求解方法、实际应用等方面深入分析这两种方法, 并展望不确定性问题解决方法的未来发展方向, 分析仍存在的挑战.

1 自动驾驶系统结构及其不确定性分析

自动驾驶系统由环境感知定位、规划决策、执行控制子模块构成, 结构如图1所示.环境感知基于车上的多传感器系统, 从里程计、惯性测量单元、雷达、相机等传感器中获得感知信息并融合, 以此表征环境.多传感器系统可为后续的航迹估算和位置估计提供车辆的运动信息.建图结果作为环境表示, 定位结果与地图建立联系.在获得车辆位姿、周围环境后, 决策规划生成多条采样轨迹并最终选择安全可行的一条轨迹, 计算得到可行速度和加速度.执行控制根据规划得出的轨迹和车辆状态进行自主驾驶.

图1 自动驾驶系统结构图Fig.1 Structure of autonomous driving system

城市环境中不确定性的因素对自动驾驶系统中的各个模块都会产生影响[4].在定位模块中, 天气和GPS灵敏度等不确定性因素都会导致车辆自身位置在世界系下出现观察误差.在感知模块中, 传感器本身固有的不确定性和环境噪声都会导致障碍物位置检测不准确甚至误检漏检, 引入碰撞风险.感知与定位会直接影响环境地图的构建与精度.雷达同样存在不确定性, 如雷达单次扫描的结果可能出现噪声引起的空间上的误检, 而两帧间的信息缺失来源于其固定存在的扫描时间.通信系统带来的不确定性会导致主体车辆与周围交通参与者及道路智能交通设施之间的交互具有滞后性和随机性, 难以精确获取其他交通参与者的意图.即使上述不确定性可通过技术性手段进行良好处理, 但控制模块仍受制于运动模型本身受到微小扰动的影响, 对噪声敏感, 难以极短时间内达到预期的加速度和速度.

鉴于上述部分模块存在的不确定性, 自动驾驶系统中起到承上启下作用的规划模块需要具备处理上游模块引入的不确定性的能力, 并且规划过程中的不确定性与其他交通参与者联系最密切, 与车辆自身的安全性密不可分.如果不能正确处理好规划中的不确定性, 可能会造成违反交通规则、碰撞等结果.在面临突发危险时, 规划能及时响应, 给出一条安全可行的轨迹或及时的预警信号, 是保证驾驶员和车辆安全的一道防线.因此, 处理规划问题中的不确定性, 是自动驾驶发展的重要一环.规划要能处理其他交通参与者交互引入的不确定性, 即在静态环境的基础上处理动态对象的时间、空间、速度、行为等方面的不确定性.

不确定性存在于自动驾驶规划应用的各类场景, 下面将从结构化环境与非结构化环境中介绍其影响.

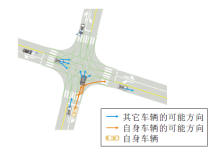
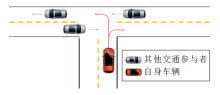
结构化环境下的无保护左转是自动驾驶中一个亟待解决的难题.即使对于人类驾驶员而言, 左转导致的事故率也是右转导致的事故率的十倍.对于自动驾驶车辆来说, 路口缺乏信号、难以预测其它车的意图、缺乏其它车辆的转向灯信号等问题导致左转过程的高度不确定性与交互性[5], 具体示意图如图 2所示.

图2 复杂路口交通场景示意图Fig.2 Sketch map of traffic scenario at complex intersection

在非结构化环境中, 多车场景的泊车问题同样具有极大的挑战性.随着城市规模增大、车辆密度变高, 2022年全国汽车保有量达到3亿辆.高峰时段车辆密度高, 邻近车位停车不规范, 停车场光线暗、空间狭小, 由于多车进入车位的意图不明确, 难以根据车辆当前速度给出准确的未来轨迹判断.并且, 其它车辆的运动多样化, 在低速情况下可能会出现急刹车、倒车等复杂运动轨迹.这些情况都会导致车辆交互问题复杂、难以预测.同样地, 车流具备高度连贯性、集体性, 驾驶员驾驶习惯不尽相同, 自身车辆与其它车辆的交互过程中对其他驾驶员的驾驶习惯不够了解, 在产生交互时难以准确预测其他交通参与者的行为变化.确定性规划在上述复杂场景中得出的路径可能会随着场景的动态变化而变得不安全.

但是不确定性规划可通过滤波器预测其他交通参与者状态, 使用概率表征可行空间, 克服其不确定性引入的碰撞风险, 在复杂环境中给出尽可能安全可靠的路径.

2 部分可观测马尔可夫决策过程

部分可观测的马尔可夫决策过程(POMDP)为不确定性环境中自动驾驶的决策和运动规划提供一种经典有效的建模方式.POMDP基于当前置信状态, 计算使未来折扣奖励最大的策略, 在特定场景下表现稳定, 能有效处理非机动车、行人等意图难以预测的交通参与者参与的场景, 在变革式自动驾驶系统中应用广泛.

然而, 随着问题规模的增大, POMDP规划问题的观测空间、状态空间, 甚至动作空间不断膨胀, 计算复杂度呈指数级增长, 限制POMDP的求解, 称为维度灾难[6, 7].同时, 迭代深度的增加导致搜索树的广度呈指数增加, 称为历史灾难[8].目前主流的POMDP求解算法通过采样、模拟等方式降低求解的复杂度, 以便在可接受的时间内获得较准确的近似解.

2.1 理论介绍

POMDP为解决自动驾驶车辆在不确定性环境中规划决策问题的建模提供一个数学框架.POMDP通常用一个八元组表示< S, A, Ω , T, O, R, γ , b0> .S表示状态空间.A表示动作空间.Ω 表示观测空间.T表示状态转移模型,

T(s, a, s')∶ =P(s'|s, a),

表示在状态s(s∈ S)下执行动作为a(a∈ A), 得到下一时刻的状态为s'(s'∈ S)的概率.在自动驾驶系统中, 下一时刻的状态s'通常还需要考虑交通参与者的运动学模型.O表示观测模型,

O(o', s', a)∶ =P(o'|s', a),

表示采取动作a、系统状态转移为s'时, 获得观测为o'(o'∈ Ω )的概率.值得注意的是, 观测信息是POMDP在马尔可夫决策过程(Markov Decision Pro-cess, MDP)的基础上新增的信息量, 目的是通过观测信息预测环境的隐藏状态.考虑到环境的不确定性, 决策主体无法通过传感器准确获取全部的系统状态, 这种部分可观测性也是POMDP的特点之一.因此, 决策主体需要利用现有的不完全观测量推测真实的环境状态量.R表示奖励模型, R(s, a)表示在状态s采取动作a获得的即时奖励.人们一般根据如下3个指标对自动驾驶的运动规划效果进行衡量:安全性、有效性、舒适性[9, 10, 11].安全性主要取决于自动驾驶车辆与动态障碍物、静态障碍物是否保持在安全距离内.安全是自动驾驶的第一要务, 因此POMDP对非安全性行为赋予巨大惩罚.有效性体现运动规划的实际效果, 由自动驾驶车辆到达目标位置耗时或车辆在行驶过程中的平均速度决定.有效性是自动驾驶运动规划追求的目标, 因此POMDP对违背有效性的自动驾驶行为进行较大的惩罚.舒适性通常由轨迹的平均曲率及自动驾驶车辆的减速次数决定.通过惩罚违反舒适性准则的行为, 自动驾驶车辆在保证安全有效行驶的前提下可为乘客提供良好的乘坐体验.γ 表示折扣系数, 决定未来决策对当前状态的影响程度.一般情况下γ < 1, 表示随着决策过程的不断迭代, 未来决策收益对当前决策的影响逐渐减小.b0表示初始信念状态, 即初始时刻环境中不确定性状态的概率分布.

考虑到环境状态的部分可观测性, POMDP引出信念状态的概念, 用于表示当前时刻环境各种可能状态的概率分布.自动驾驶系统中的不确定性可大体分为两类:1)系统硬件自身带来的不确定性, 包括感知和控制的不确定性; 2)其他交通参与者行为意图的不确定性.针对第1种不确定性, POMDP通常引入高斯噪声进行不确定性建模.针对第2种不确定性, POMDP通常将不同交通参与者的行为意图建模成不可观测的离散状态, 如运动轨迹、速度、加速度、道路保持、换道等, 并对每种不可观测状态赋予概率, 模拟意图行为的不确定性.

将问题建模成POMDP的最终目的是获取在当前状态下的最优策略π * .π * 可表示为一个动作序列(a1, a2, …, an), 其中n表示所需的决策次数.策略的优劣取决于动作序列获得的未来折扣收益, 贝尔曼最优性准则常被用于对当前信念状态的最优值进行更新.

2.2 求解方法

2.2.1 离线算法

离线算法在离线情况下完成模型求解, 与决策主体的在线决策过程是分离的.离线求解算法可计算决策体每种信念状态下的最优策略.在决策主体进行决策时, 只需要根据当前信念状态查询得到最优动作并执行即可.

离线算法的优势在于最优策略的计算不占用在线决策的时间, 可保证决策的实时性, 但该算法需要处理大范围信念状态空间, 求解时间较长, 实用性较低.为了处理这种低效的精确求解问题, 有学者提出可加快运算速度的近似方法.基于点的值迭代算法是典型的离线近似算法之一, 基本思想是只考虑部分可达的信念状态以减小信念状态空间的大小, 从而减小运算量.考虑到最优值函数是分段线性的, 因此部分信念状态通常对整体的信念状态空间具有较好的模拟[12].在基于点的值迭代的思想基础上学者们提出一系列相关的算法, 如PBVI(Point-Based Value Iteration)[8]、Perseus[13]、HSVI(Heuristic Search Value Iteration)[14]等.

2.2.2 在线算法

离线算法只能针对静态的环境模型进行处理, 而对环境中的动态因素缺乏处理能力.

不同于离线算法计算每种信念状态下的最优策略, 在线算法只考虑当前所处的信念状态及从当前信念状态可达的其它信念状态.在线算法分为两个阶段:规划阶段(策略计算)和执行阶段.整个决策过程中规划与执行交替进行.

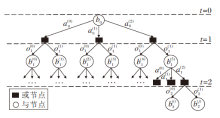
规划阶段分为搜索树构建和回溯两步.POMDP构建的搜索树又称与或树, 由与节点(AND-Nodes), 或节点(OR-Nodes)构成, 一个典型的与或树如图3所示.以当前信念状态b0为根节点, 基于根节点信念状态遍历所有动作at, 得到相应的OR-Nodes.基于每个OR-Nodes, 考虑所有可能的观测ot, 并更新信念状态b, 获取新的信念状态节点.以此类推, 直到达到事先设定的搜索深度, 搜索树构建完成.构建完成后利用贝尔曼最优性原则从叶子节点开始对搜索树进行回溯, 对回溯路径上各个信念状态节点的最优值进行更新.叶子节点的最优值可采用离线算法[15, 16, 17]或蒙特卡洛模拟(Monte-Carlo Simulation, MCS)的方式进行计算[18, 19, 20].

图3 POMDP搜索树示意图[9]Fig.3 Sketch map of POMDP search tree[9]

尽管相比离线算法, 一般的在线算法计算量已大幅降低, 并且对动态环境中的决策也有较好效果, 但依然需要处理庞大的动作空间及观测空间, 影响实时性.研究者们通常关注近似算法, 在保证一定的决策准确度的前提下降低运算量.

在线近似算法主要分为3类:分支与边界裁剪算法[21]、启发式算法[22, 23, 24]、基于蒙特卡洛模拟的算法.

分支与边界裁剪算法的基本思想在于通过对比不同节点最优值函数的下界和上界, 将已知次优的树分支进行裁剪, 避免进行不必要的拓展.首先, 采用离线算法计算叶子节点值的上界(MDP[25], QMDP-net[26], FIB(Fast Informed Bound)[27])与下界[28].然后, 利用贝尔曼最优性准则, 通过反向回溯更新搜索树内部节点边界值.

在进行树搜索时, 倘若在当前信念状态b下执行动作a获得的值函数下界大于执行动作a'时获得的值函数的上界, 那么可认为在信念状态b下动作a'是次优的, 因此可将动作a'及其分支进行裁剪, 降低搜索树的复杂度, 提高树搜索效率.

不同于分支与边界搜索算法, 启发式算法通过启发式信息选取最具有潜力的分支进行搜索, 实现通过扩展更少的节点以获取一个更好的决策的目的.在启发式算法中, 每个叶子节点存储一个启发值, 该启发值表示该叶子节点被扩展的价值.与此同时, 搜索树的内部节点存储当前树分支内具有最优启发值节点的索引及最优值.在每次迭代过程中选取启发值最大的节点进行扩展(一般扩展一层), 再采用动态规划算法, 对拓展节点的祖先节点进行启发值更新.

基于此基本框架, 学者们相继提出各种启发式算法, 如Satia and Lave[29]、BI-POMDP(Bounded, Incremental POMDP)[30]、AEMS(Anytime Error Minimi-zation Search)[31]、HSVI等.这些算法主要的不同之处在于启发函数的设计.启发函数设计的合理性影响树搜索的效率, 从而进一步影响整个算法的求解速度.

一般的求解算法通常需要对POMDP问题进行准确建模, 通过建立的模型对信念状态进行前向模拟以计算未来折扣奖励.然而, 建模实际问题极具挑战性, 模型的准确性对决策性能影响较大.研究者们寻求一种更简单的方法评估当前策略的优劣, 即蒙特卡洛方法, 使用大量随机事件逼近真实情况.在蒙特卡洛模拟的过程中, 系统的状态转移模型、观测模型及奖励模型被统一建模成黑盒.

尽管蒙特卡洛模拟可近似估计某个状态的好坏, 但大规模的模拟过程需要消耗大量时间, 因此模拟所有状态不具备可行性.蒙特卡洛树搜索选择最具有潜力与价值的节点进行蒙特卡洛模拟, 从而使搜索树在较好的策略上进行扩展.蒙特卡洛树搜索算法主要包含4步:选择、扩展、仿真、反向传播.部分可观测的蒙特卡洛规划(Partially Observable Monte-Carlo Planning, POMCP)交替进行蒙特卡洛树搜索和信念状态更新的过程.

POMCP通过对信念状态空间的采样避免POMDP的维度灾难, 通过黑盒进行状态转移和观测模拟以避免POMDP的历史灾难.然而, POMCP有时表现过于贪婪, 并且在最坏情况下的表现极其糟糕[32].

DESPOT(Determined Sparse Partially Observable Tree)在POMCP上进行进一步的改进与优化.与PO-MCP类似, DESPOT通过对状态的采样及前向仿真模拟避免决策过程中的维度灾难与历史灾难.DES-POT将信念状态采样数限定在一个较小的值, 并将采样获取的状态称为场景(Scenarios).

前向模拟生成的轨迹数主要受到动作空间大小的影响, 与观测空间无关.DESPOT限制采样场景数, 在较小的动作空间内生成稀疏搜索树.在稀疏搜索树构建完成后, 与POMCP类似, DESPOT循环进行树搜索、节点扩展与仿真, 最后再向根节点回溯.

离线算法与在线算法的优缺点对比如表1所示.

表1 离线方法与在线方法优缺点对比 Table 1 Advantages and disadvantages of offline and online methods

2.2.3 强化学习

强化学习能让智能体在与环境的交互中自主学习, 通过最大化奖励的方式让智能体学会如何决策.Mnih等[33]使用的深度强化学习技术DQN(Deep Q-Network)结合深度学习极强的感知能力和强化学习自主学习、决策的能力, 更广泛地应用于如运动规划、决策控制等多个领域.在处理不确定性问题的迭代过程中, 强化学习的目标就是使Agent通过最大化累计奖励rt学习最优化策略Π * , 获得观测到最优动作的映射.

大多数强化学习问题都假设环境的状态在每个时间步长下都是完全可观测的, 针对MDP描述的问题, 强化学习已有很多经典算法.例如:1)基于价值(Value-Base)的算法, Dueling DQN[34]、Double Q-Learning[35]、Rainbow[36]等; 2)基于策略梯度(Policy-Base)的算法, Actor-Critic[37]、DDPG(Deep Deter-ministic Policy Gradient)[38]等, 都取得较优效果.

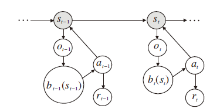
但是对于现实环境来说, 智能体一般由其搭载的传感器感知环境, 在每个状态st下, 智能体由其传感器获得观测ot.然而, 由于传感器的误差、遮挡、噪声等不确定性因素, 观测ot无法代替状态st给出使智能体获得做出决策的所有环境信息.在这种情况下, 应考虑POMDP.POMDP决策过程如图4所示.POMDP是在MDP上增加观测空间Ω 、观测模型O和信念b, 让智能体通过不完全观测的数据ot推测真实状态st.

图4 POMDP决策过程示意图Fig.4 Sketch map of POMDP decision-making process

POMDP的主要挑战在于如何通过不完全的观测推测信念状态, 有效的信念状态是获取POMDP最优策略的基础.

为了减小信念状态与真实状态之间的误差, 目前有两种主流的做法:1)通过循环神经网络(Recur-rent Neural Network, RNN)记录历史观测和动作, 为智能体提供更多的信息, 此方法隐式地包含对信念状态的推理, 不仅依靠当前观测选取动作, 可有效处理部分POMDP问题.但是这种隐式包含给RNN带来沉重负担, 可解释性较弱, 难以在复杂的任务中获取有效的最优策略.2)在强化学习架构中引入模型以推理信念状态, 使POMDP问题可转换为MDP问题进行训练, 从而获得最优策略Π * .

在强化学习中引入信念状态作为输入的一部分的思想在文献[39]中被提出, 并且深度信念Q网络(Deep Belief-State Q-Networks, DBQN)也被提出.DBQN大致沿用DQN的总体构架, 通过Q-Learning的方式更新网络权重参数, 损失函数为:

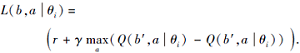
DBQN网络结构如图 5所示.网络的输入层由智能体的信念状态向量和完全可观测向量构成, 而以往的DQN输入由MDP中的状态表述, DBQN通过在输入中添加信念状态以寻找最优策略, 这使DBQN具有可有效应对POMDP场景的能力, 并且在Tiger与Rock Sample两款游戏中都获得优于DQN的效果.

图5 DBQN网络结构图[39]Fig.5 Network structure of DBQN[39]

DBQN的不足之处在于每次在执行动作之前, 当前的信念状态需要被计算后输入网络中, 而当前的信念状态又没有具体的推理模型, 因此DBQN只能满足有模型(T, O已知)的POMDP问题.

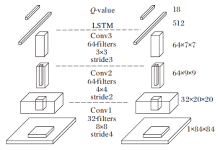
Hausknecht等[40]将POMDP问题中的历史观测信息由RNN记录下来, 提出DRQN(Deep Recurrent Q-Network), 适用于无模型的POMDP场景.DRQN网络结构如图 6所示.DRQN最小限度修改原DQN网络结构, 仅仅将DQN中第1个全连接层换成相同大小的长短期记忆网络(Long Short-Term Memory, LSTM)层[41].相比RNN, LSTM结构储存更多的历史信息, 使网络隐式推理更准确的信念状态.

图6 DRQN网络结构图[40]Fig.6 Network structure of DRQN[40]

继承DRQN的思想, Foerster等[42]提出DDRQN (Deep Distributed Recurrent Q-Network).Zhu等[43]提出ADRQN(Action-Specific Deep Recurrent Q-Net-work).DDRQN和ADRQN都认为循环网络中记录的信息不应仅包含历史的观测(ot, ot-1, ot-2…), 也应包含历史的动作信息(at, at-1, at-2, …), 这样有助于更好地推断当前的信念状态.不同之处在于DDRQN分别输入历史动作序列和历史观测序列进行解耦, 而ADQRN将历史观测和历史动作组合成观测-动作对输入, 体现时序条件下历史观测与历史动作的相关信息.提供历史动作信息的DDRQN和ADRQN更有助于智能体学习最优策略Π * .实验证实, 在Pong、Frostbite、Asteroids等游戏中, 提供历史动作信息的DDRQN和ADRQN表现更优, 验证在RNN中包含更多的有效历史信息有助于智能体在POMDP场景中更好地学习最优策略Π * .

第2种方法根据具体模型推理更新信念状态, 更具有可解释性, 但是总体性能较强依赖于推理模型的性能, 整体结构更复杂.Igl 等[44]提出DVRL(Deep Variational Reinforcement Learning), 基于AESMC(Auto-Encoding Sequential Monte Carlo)[45]的ELBO(Evidence Lower Bound)近似方法将归纳偏差合并到策略网络结构中.整体框架使用Actor-Critic架构, 利用学习的模型推断信念状态, 应对POMDP环境.信念更新函数为:

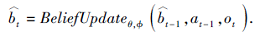
实验表明, DVRL优于DRQN、ADRQN等基于RNN表述信念状态的方法.此外, Wang等[46]提出DualSMC(Dual Sequential Monte Carlo), 将POMDP滤波和规划问题转换为两个密切相关的序列蒙特卡罗过程(Sequential Monte Carlo, SMC), 通过蒙特卡洛滤波直接规划一个近似的信念以明确表示信念分布, 并且按策略训练的方法训练信念状态表述滤波器.Singh 等[47]提出SWB(Structured World Belief), 通过SMC推断为在POMDP环境中提供以对象为中心的结构化世界信念, 帮助智能体学习最优策略.Chen等[48]提出FORBES(Flow-Based Recurrent Belief State Model), 将标准化流[49]纳入变分推理过程, 学习POMDP的一般连续信念状态, 应对POMDP环境, 又将FORBES应用于POMDP强化学习模型, 采用Actor-Critic架构学习最优策略, 使用POMDP提供的信念状态进行最优策略学习, 避免类似RNN的观测模型整合, 并且在DeepMind的视觉-运动控制任务[50]中取得较优效果.

2.3 不确定性下的应用场景

POMDP为自动驾驶环境中不确定性因素的建模提供一种科学有效的方式.随着相关求解算法的不断发展与优化, POMDP在自动驾驶汽车的运动规划中发挥越来越重要的作用, 应用于多个场景.

2.3.1 行人交互环境

行人作为城市道路环境的重要组成部分, 具有随机性和集体特征, 给运动规划场景带来大量的不确定性.

人群环境的运动规划问题需要处理的主要不确定因素是行人的意图.行人意图决定下一时刻行人的运动轨迹, 这对车辆运动规划来说十分重要.一般情况下, 人群中运动规划问题主要被处理为局部动态避障问题, 如社会力(Social Force)算法[51, 52, 53].该算法构建目标点对车辆的引力及行人对车辆的斥力, 通过虚拟力的方式引导车辆运动.然而这种方法容易陷入局部最优, 并且在密集的人群中很难规划一条完全无碰撞的路径, 容易导致穿梭在人群中的车辆频繁刹停, 难以实现安全并快速的通行.

Bai等[9]设计一个两层的架构, 处理人群环境中自动驾驶的决策与运动规划问题.上层采用Hybrid A* [54]进行路径规划, 并采用纯追踪算法[55]计算车的前轮转角.底层采用POMDP进行速度规划, 输出车辆的加速度.POMDP中将行人的意图作为不可观测量, 建模为一个目标位置, 并采用贝叶斯规则对该信念状态进行更新.最后, 采用DESPOT进行模型求解, 整个决策过程以一个接近实时的频率运行.实验表明, 该方案在简单特定的行人运动场景中具有不错效果.

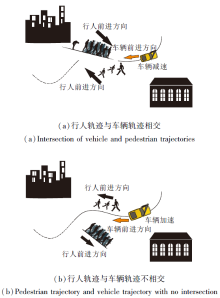
文献[9]方法在人群中的运动规划结果如图 7所示.(a)中行人意图穿越车辆预测路线, 车辆减速.(b)中尽管在车辆预测路线附近依然有行人, 但是行人意图往远离车辆预测路线的方向运动, 此时车辆加速.相比传统的反应式避障方法, 这种考虑行人不确定性的POMDP具有更小的危险性(Risk)、通过时间(Time)和总加速度(Total Acceleration), 即在安全性、有效性及舒适性三个指标上都具有较大的优势.但在行人状态转移模型构建过程中, 模型仅简单假设行人向目标位置沿直线运动, 导致难以处理行人的复杂运动场景.

图7 人群中的运动规划结果[9]Fig.7 Result of motion planning in the crowd[9]

Luo等[10]提出PORCA(Pedestrian Optimal Reci-procal Collision Avoidance), 用于预测行人的运动轨迹.PORCA引入更复杂的行人运动模型, 根据行人意图及行人之间、行人与车辆之间的交互, 对行人短期运动轨迹进行准确预测.然而, 两层处理架构解耦前轮转角与车辆加速度控制, 不利于模拟真实环境中的复杂驾驶行为.

Cai等[11]提出LeTS-Drive(Driving in a Crowd by Learning from Tree Search), 结合POMDP与深度学习, 实现自动驾驶车辆在密集人群中的运动与导航.为了模拟复杂驾驶行为, LeTS-Drive构建一个二维联合动作空间, 同时考虑车的前轮转角与加速度.在搜索树构建过程中, 基于HyP-DESPOT(Hybrid Parallel DESPOT)[56], LeTS-Drive使用预先训练好的策略与值网络引导动作的选择, 进一步加速搜索树构建效率.然而, 神经网络的复杂性影响在线搜索的效率, 因此需要更有效的策略和价值函数表示.当网络学习的策略难以推广到不同的地图与主体车辆行为上时, 需要进一步拓展模型的训练环境.

2.3.2 路口车辆交互环境

城市道路无交通信号灯的交叉路口是自动驾驶中一个典型的不确定性场景.考虑到没有交通信号灯的规则约束, 路口中其它车辆的行为变得复杂、难以预测, 这对交通路口的安全且快速通行造成很大的挑战, 具体如图 8所示.

图8 无交通信号灯的交叉路口下的运动规划Fig.8 Motion planning of intersection without traffic lights

Bouton等[57]使用POMDP对通过无交通信号灯路口的自动驾驶车辆进行速度规划.路口中其它车辆的不确定性行为被建模成两类:恒定速度(Con-stant Velocity)与恒定加速度(Constant Acceleration).模型采用IMM(Interacting Multiple Model)进行信念状态更新, 采用POMCP进行求解.将POMCP的求解结果分别与一种简单的启发式策略TTC(Time to Collision)[57]和一种随机策略进行对比, 对比结果可知, 自动驾驶车辆在无交通信号灯的十字路口进行左转或右转时, POMCP在保证极高的通过率(Success Rate)和极低的碰撞率(Collision Rate)的前提下, 具有最短的通过时间(Time to Cross).

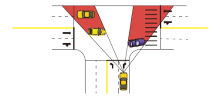
由于交叉路口结构的特殊性, 车辆的视线常受到路口中其它车辆的遮挡, 从而产生视野盲区, 如图 9所示.

图9 视野受限的路口车辆Fig.9 Vehicles with limited vision at intersection

视野盲区的潜在障碍物存在严重的安全隐患, 是一个不容忽视的因素.Lin等[58]基于POMDP对存在遮挡的交叉路口的决策过程进行建模, 将其它车辆不同运动轨迹的概率分布作为信念状态, 采用贝叶斯规则进行信念状态追踪.同时, 为了应对视野盲区存在的潜在风险, 引入虚拟障碍物的概念, 模拟在盲区中可能出现的其它车辆, 大幅提升决策的安全性与可靠性.类似地, Hubmann等[59]利用信念状态, 低维表示可能被遮挡的隐藏车辆, 并包含这些车辆的未知路线及在这些路线上的概率, 最终构成一个其它车辆的可达区域集合.

Pruekprasert 等[60]提出基于意图感知的无交通信号路口的自动驾驶, 交通参与者的意图划分为两类:纵向意图(刹车与停止)和横向意图(预测轨迹集合).模型采用动态贝叶斯网络(Dynamic Bayesian Network, DBN)进行意图追踪, 并采用DESPOT进行模型求解.实验表明此模型使车辆在路口具有较好的通过性, 同时可应对路口中有车辆、行人等多种异构智能体的情形.

2.3.3 车道变更环境

车道变更往往发生在前方车辆速度较低, 但占据整个车道, 影响自身车辆行驶的情况下.该场景中的不确定性因素主要体现在周围车辆意图的不确定性.周围车辆意图极大影响车道变更的可行性与安全性.

Meghjani等[61]基于POMDP, 提出基于道路上下文信息及意图理解的运动规划算法, 算法中信念状态由车道保持、左换道和右换道这3种意图的概率分布表示, 并训练一个LSTM网络, 帮助信念状态的更新.被超车辆的未来轨迹根据其历史轨迹、道路上下文信息及车辆意图进行预测.算法采用DESP-OT进行求解, 输出当前最优的换道动作.超车示意图如图10所示, (a)中主体车辆试图左换道超越前方慢速车辆, (b)中前方车辆左换道以阻止主体车辆超车, (c)中主体车辆察觉左侧车道阻塞且前方无车辆, 试图回到中间车道继续高速行驶, (d)中背景车辆未发现主体车道的超车意向, 回到中间车道慢速行驶, 主体车辆成功左换道超车.在换道场景中, 考虑其他交通参与者意图的POMDP换道成功率达到100%, 同时在换道过程中耗时最短.

图10 超车示意图Fig.10 Sketch map of overtaking

Ulbrich 等[62]基于自身所处车道及左右2侧车道中所有车辆运动的动态表示, 利用2个信号处理网络分别判断车道是否具备变更可能的网络和判断变更车道是否有益, 输出到POMDP中进行决策.研究者将所有随机变量聚合为特定感兴趣区域的一个度量, 使用模糊逻辑规则描述过程.Mentasti 等[63]在MDP中嵌入连续状态分层贝叶斯转移模型.通过求解MDP, 可自动导出双车道公路场景中自动驾驶汽车与多辆其它汽车的决策.另一种方法是采用混合可观测的马尔可夫决策过程对超车场景进行建模, 考虑测量和行动的不确定性, 优化超车决策, 为双向道路超车问题提供解决方案.

在未来的研究中, 需要评估更多情况, 如跟车行为.在多车道上行驶时, 加速/减速动作需要扩展为变道动作.由于系统使用低级状态空间, 因此不需要为这些任务定义新的模型或符号状态.可针对所有可控道路用户的集中POMDP规划和联合行动, 实现多辆自动驾驶车辆的协同驾驶.在部分可观测的不确定性环境中运行的自主代理通常需要同时优化预期性能和限制违反安全约束的风险.这两个问题可同时建模为CC-POMDP(Chance-Constrained POMDP)[64], 约束条件尤为重要.SSC(Unified Spatio-Temporal Semantic Corridor)[65]将约束分为硬约束和可松弛约束, 硬约束用于保证安全性, 如碰撞距离, 可松弛约束用于保证舒适性和类人程度, 如换道所需要的时间.对于人类驾驶员, 面临交通规则与危险环境的冲突, 通过直觉推理可做出规避风险的判断, 而对于自动驾驶车辆, 对于多个相悖的约束, 往往会导致缺乏可行空间, 在无法进行规划的情况下即使急停也难以保证安全, 尤其是在上述车流密集的复杂环境内.因此, 适当地松弛部分约束可有效应对极端不确定性环境内的安全性问题.

3 概率占用栅格图

概率占用栅格图(POGM)常用于表示从感知得到的环境信息和描述可行空间.利用感知信息表征真实世界的过程会引入不确定性, 该过程可建模为估计理论问题.POGM本身能提供明确编码的空间信息和相关不确定性, 导出确定性体素模型或更高级别的几何表示[66].环境表示的适用性直接影响规划获取相关信息的难易程度, POGM包含的不确定性信息容易处理, 因此自动驾驶规划任务在占用栅格图框架内可高效完成.占用栅格图具有多种表达形式, 常见的有二值化表达形式, 一个网格仅有占用(Occupied)与空闲(Free)两种状态.这种表示会损失大量信息, 不利于不确定性环境下的规划决策过程.

3.1 理论基础

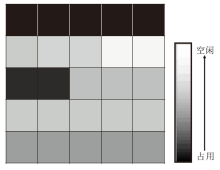
概率占用栅格图作为一种环境表征方法, 表示形式如图 11所示.虽然POGM从栅格地图发展而来, 但是比仅有占用/空闲两种状态的栅格地图, 概率的表示形式更适用于碰撞风险的衡量.因此, POGM具备环境表征抽象性、碰撞风险更优性的特征.多传感器融合是当今环境感知的主流形式, 模型获取不同维度、不同角度的感知信息以表示环境.多传感器采集的数据融合后形成一种统一的紧凑型表征模型, 用于表达当前的行驶环境[67, 68].

图11 POGM表示形式Fig.11 Representation of POGM

基于贝叶斯滤波的占用栅格模型与其相关的改进模型是一种典型的紧凑型表征模型.Elfes等[69]将传感器信息解释为栅格单元值以构建占用栅格.当将传感器数据解释为占用信息时, 不可避免地引入未知部分和误差导致的不确定性.未知部分的产生是由于靠前障碍物的遮挡, 导致障碍物后的区域不能被感知到, 误差来自噪声和不精确的姿态估计[70].

POGM包含对应栅格的占用率.对于一个栅格, s=1表示对应栅格为占用状态, 否则, s=0表示空闲状态, p(s=1)和p(s=0)分别表示该栅格处于占用或空闲状态的概率, 二者之和为1.因此, 可用一个值同时表示出二者, 即两者比值表示该点状态:

Odd(s)= p(s=1)p(s=0).

为了更方便的表示, 对于每个点, 一旦得到一个测量值(Measurement)z, 需要利用贝叶斯法则进行一次状态更新.更新前状态为Odd(s), 更新后

Odd(s|z)= p(s=1z)p(s=0z).

更新过程如下:

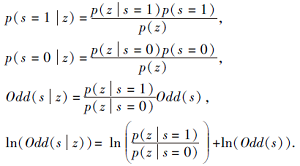
以此分离测量值, 前者称为测量值的模型, 记为lomeas.

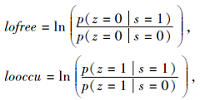
这两种表示均为定值.这种表示使用概率的形式, 描述感知过程中的不确定性, 可更好地解决连续时刻内出现的冲突结果, 更新规则简单.在这种描述下, lofree越大, looccu越小, 则该栅格为空闲状态的置信度越高.

3.2 求解方法

构建好POGM后, 在其上的求解方法同常规栅格图类似, 可分为4类:基于采样的方法、基于搜索的方法、插值曲线法、数值优化方法.基于采样的方法是在空间内采样得到可行路径点.基于搜索的方法是对网格节点进行搜索, 得到可行的节点连接方式.插值曲线法在已知路径锚点间以螺线、多项式曲线的轨迹形式进行平滑连接, 得到符合车辆行驶动力学约束和运动学约束的平滑曲线.数值优化方法设定合适的目标函数, 近似/精确求解该优化问题, 得到目标轨迹.Tsardoulias等[71]提出若干指标, 对比后得出空间采样方法最适合POGM.

基于采样的方法以快速扩展随机树(Rapidly-Exploring Random Trees, RRT)及其各类优化变种方法为典型代表.自RRT提出后, 常应用于解决非凸高维空间的快速搜索、静态障碍物和差分运动约束问题, 并且作为局部规划时可考虑更大范围内的障碍物.

RRT通常认为在可行空间内, 所有节点可达, 所以在全部节点中进行随机采样.基于样条的RRT* (Optimal RRT)通过B样条曲线扩展随机树[72], 在可实现有约束情况下进行规划, 同时也可在树扩展阶段检查碰撞, 判断角加速度是否可达, 其中扩展阶段检查碰撞的范围大小rball随着节点数量的增加而缩小.具体算法步骤如下所示.

算法 基于样条的RRT* 算法[72]

输入 RRT树, 初始节点

输出 符合渐进最优性的路径

初始化RRT树

While xnew与终点距离大于距离限制 do

While xnew的邻近节点非空 do

在设定的环境内部产生随机点xnew

建立随机点的周围的最近邻节点xnearest

End while

将延伸节点加入xnew

If xnew与xnearest无碰撞 then

xnew周围半径为rball的边界内的节点存入Xnear

For xnear∈ Xneardo

xnew=xnearest

cmin=cost(xnearest)+cost(xnew, xnearest)

If (xnew, xnearest)无碰撞且可行且

cost(xnear)+cost(xnew, xnear)< cminthen

xmin=xnear

cmin=cost(xnear)+cost(xnew, xnear)

End if

End for

For xnear∈ Xneardo

If (xnew, xnear)安全可行且

cost(xnew)+cost(xnew, xnear)< cost(xnear) then

xparent=parent(xnear)

End if

End for

End if

If xnew与终点距离小于距离限制 then

return RRT树

End if

End while

Reachability Guided RRT[73]可消除不准确的距离对RRT探索能力的影响, 计算树中节点的可达集, 当采样点到节点的距离大于采样点到该节点可达集的距离时, 该节点才有可能被选中进行扩展.

RRT还有许多其它优化, 如Anytime[74], 整体思想是将树的生长方向引导到障碍物稀疏的区域, 仍是在空间中进行采样.Risk-RRT(Risk RRT)[75]利用动态障碍物的未来轨迹预测, 并将其以高斯分布的形式表征在栅格图上, 将预测与规划进行集成, 即先得到障碍物的预测轨迹, 并在一定半径内根据高斯分布得到对应栅格的占用率, 以碰撞风险为导向, 结合规划方法与动态环境的感知和预测的概率碰撞风险函数, 即在扩展结点时考虑Risk是否符合满足阈值.考虑到动态障碍物间的相互作用, 在对应栅格上不能直接进行概率上的叠加, 而又难以获取联合概率密度分布.Bi-Risk-RRT(Bidirectional Risk-RRT)[76]在第一阶段, 两棵树相互生长.在第二阶段, 反向树生成启发式轨迹, 正向树根据启发式采样分布增长.Bi-Risk-RRT比Risk-RRT运算速度更快, 敏感性更低, 最大线速度对轨迹长度变化的相关程度也更低.而且, 启发式方法比尝试求解TBVP(Two-Point Boun-dary Value Problem)的树-树连接方法更鲁棒.

与之不同的是, 动态窗口法(Dynamic Window Approach, DWA)在速度空间内采样.DWA中采样多组速度(v, w), 并模拟这些速度在一定时间内的运动轨迹.通过评价函数对这些轨迹进行评价, 选取最优轨迹对应的(v, w)驱动车辆运动.在非结构化环境中, 通常采取DWA与全局规划(如A* )结合, 应对自动泊车的复杂场景.

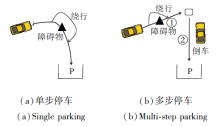
除了常见的城市道路交通环境, 自动驾驶还可应用于取代危险环境中工作的驾驶人员, 如灾后的救援车辆.援建车辆需要在不确定性高、障碍物多、情况复杂的环境中导航到指定点停车.Yang等[77]提出使用A* 与DWA的单步停车策略, 即车头向内停入车位, 和两步停车策略, 即先到达某个中间节点, 再通过倒车的方式, 车头向外停入车位.具体如图12所示.

图12 单步停车与多步停车Fig.12 Single and multi-step parking

Pan等[78]提出D2WA(″Dynamic″ DWA), 可应对动态的不确定性环境, 与动态障碍物相关的代价函数的权重根据不同的障碍物状态进行动态调整, 可避免不必要的避碰, 提高运动规划者对动态障碍物的可预测性.

上述的基于采样的方法往往难以在有限迭代中得到最优路径, 而基于搜索的方法发展已较成熟, 具有解析完备性和解析最优性.Koenig等[79]提出一种增量算法, 用于推广具有任意边插入、边删除和边长度变化的图中的最短路径问题.Stentz等[80]提出Dstar, 在部分已知的环境中实现最佳、有效的重新规划, 当检测到地图中的变化时, 不是重新计算整个地图的最佳路径, 而是检查一组减少的单元, 并逐步更新到最佳路径.这里的增量利用以前计划的结果生成新的规划结果, 可加快速度.然而, 在可用时间内找到绝对最优的路径是不可能的.

由于占用栅格图维数较低, 所以网格节点数较多, 运算效率较低.预处理占用栅格图使其变得更稀疏, 可有效改善这种情况.研究者们通常采用k-PRM[81]和PRM* [81]进行降采样.这两种方法都是通过节点自身的邻居关系降低节点数目.k-PRM仅取决于自身所在节点和设置的视窗大小, PRM* 虽然选择半径会发生改变, 但其对不同的环境取决于总的点数, 不具有场景间的区分度.3D重建后的相机在弱光条件下容易产生伪影.对于这种情况, 障碍物会出现位置上的不确定性, 容易导致多检、误检.这种感知导致的不确定性环境表征给障碍物碰撞风险的衡量带来极大的不确定性[83].

Saroya等[84]提出GNG(Growing Neural Gas), 拥有比PRM* 更快的速度, 利用同源特征影响采样过程, 使其朝着难以通过的区域增长, 确保通过狭窄通道的路线图的连通性.GNG引入的抽样方法之一是通过POGM直接得到映射概率分布, 另一抽样方法根据同源特征位置创建高斯混合分布以得到映射概率分布.

Ok等[85]提出Voronoi不确定性场, 以便在不确定性情况下进行路径规划.考虑环境中观察的障碍物的不确定性, 并根据它们与自身的距离及其位置不确定性分配排斥力.来自Voronoi节点的吸引力和来自不确定性偏向势场的排斥力形成Voronoi不确定性场(Voronoi Uncertainty Fields, VUF).

McLeod等[86]基于RAMP(Real-Time Adaptive Motion Planning)框架, 随机初始化一组轨迹, 使用多目标评价函数确定最佳轨迹.当智能体沿着轨迹移动时, 同时更新当前位置到终点的轨迹集, 并从中选择最优的轨迹, 以此适应新感知的行驶环境的变化.RAMP框架并行处理轨迹集的更新、代价函数的最优计算、控制智能体沿轨迹移动三个过程, 使用的代价函数合并真实数据和概率数据, 评价智能体在环境中未见区域的轨迹, 提高实时执行的能力.

因为POGM本身的概率特性, 因此也常用机会约束规划处理此类问题.机会约束用于衡量障碍物碰撞概率, 求解方法在运动规划中通常转化为确定性进行求解.

3.3 具体应用

POGM的构建与建图方法密不可分, Jimé nez等[87]优化从雷达点云得到占用率的建图方法.Sun等[88]利用语义信息及地形, 使用多张小的POGM拼接而成, 保证POGM的分辨率.并且, 具备预测特征的地图也为未知的不确定性环境中的运动规划提供有力工具, 克服对未观察到的环境结构进行推理的能力有限的问题[89, 90, 91].Wang等[92]使用自监督学习方法, 通过模拟导航轨迹增强数据, 将预测推广到3D占用栅格图, 保证安全高效的规划.

McLeod等[86]利用过去的经验, 基于Hilbert Maps框架, 从深度信息中学习以预测概率占用栅格图的占用率.该方法将深度数据投影到由近似核函数定义的高维希尔伯特空间中, 然后在该高维空间中学习线性逻辑回归模型, 结果是一个sigmoid似然判别模型, 可预测欧几里得空间中某点被占用的概率.单个栅格未被占用的概率为:

P(y=-1|x, w)= 11+exp(wTϕ(x)),

其中, ϕ (x)表示位置x的特征向量, w表示学习的参数向量.

文献[86]方法可结合学习到的信息和真实的障碍物感知信息, 为那些被遮挡的环境区域提供有用的信息, 得到POGM, 为智能体提供RAMP框架下更优的初始轨迹.相比原始的确定性RAMP框架, 文献[86]方法在高占用率区域会生成更少的初始轨迹, 在行驶过程中切换轨迹的偏差更小.

运动规划的目标是找到一个轨迹, 使某些代价函数最小化, 满足运动学约束, 并避免碰撞.POGM用于确保规划得出的轨迹没有碰撞.然而, 多数规划方法都假设初始状态是完全已知的, 但由于传感器噪声的存在, 在现实世界中往往无法给出完全确定的状态.

为了解决此类问题, 可用高斯概率分布描述不确定性, 使用更大的膨胀体积近似对象, 在此基础上快速执行碰撞检测[93].但是, 扩大的边界体积通常会对碰撞概率夸大估计.因此, 在复杂的环境中导航, 这种表示方法往往会导致可行空间缩小, 规划可能会因此得到次优方案.

为了处理不确定性环境下的碰撞检测问题, 通常将自动驾驶汽车与障碍物的位置使用具有无界概率分布形式的随机变量描述风险感知运动规划算法[94], 适用于最小化碰撞概率, 这里的不确定性碰撞可能是车辆和障碍物定位不精确、车辆自身或动态障碍物的动力学模型不准确, 甚至可能是噪声干扰导致的碰撞.因此在文献[95]中提出风险感知成本函数, 将高斯过程(Gaussian Process, GP)后验的风险度量转换为用于规划的成本函数.基于采样的在线运动规划算法中风险函数的应用可考虑到轨迹长度、平滑度、与障碍物的距离.利用概率栅格图处理多传感器融合后信息, 进行车道占用概率判断, 综合车道内的占用概率, 表征车道的可行性, 并利用贝叶斯网络在图上进行辅助换道决策[68, 96, 97].Artuñ edo等[98]创建感知栅格, 并将地图信息和道路限制添加到栅格中, 可区分自由的可导航空间或非可导航空间, 以及使用车对车通信获得的动态障碍物速度.栅格图可将车道信息、动静态障碍物信息集成到通用表达里.

Lau等[99]将栅格图转化为距离图, 初始状态下空闲栅格距离障碍物的欧几里得距离为正无穷.因为有边界和障碍物的存在, 减小内部未被占用栅格与最近障碍物点的距离, 即从障碍物栅格开始, 逐步向外扩散更新, 计算新的最近障碍物坐标与距离, 距离越近颜色越深.当所有栅格都被更新后, 距离图建立完成.由于障碍物的消失, 其附近的栅格中保存的最近障碍物距离被更新为无穷, 此类栅格的状态更新是一个距离增大(Raise)的过程.类似地, 因为新的障碍物出现, 周围的栅格保存的最近障碍物距离被重新计算, 所以这些栅格的状态更新是一个距离减小(Lower)的过程.当Raise和Lower的过程相遇, Lower处理过的栅格不会受影响, 但对于Raise处理过的栅格, 要考虑新出现的障碍物对其的影响, 需重新计算最近障碍物的距离, 所以Raise过程结束, 转变为Lower过程.当两类过程不再更新时, 新的距离图更新结束.该更新过程与GVD(Generalized Voro-noi Diagrams)的更新同步进行, 但其只更新障碍物附近的栅格, 不更新静态障碍物或固有边界, 避免遍历全部栅格, 所以这是一个增量更新的过程, 访问栅格较少, 实时性较好.

Lü zow等[100]设计可微分框架, 规划可行的轨迹, 使碰撞风险最小化.将栅格图作为深度卷积神经网络的输入, 可对交通参与者的交互进行隐式建模.通过给定的初始密度分布集中随机采样初始状态, 并使用分箱方法在占用图上为每个预测障碍物位置分配相应的单元, 对落入同一单元的所有样本的密度取平均值, 最后归一化占用率.

Banfi等[101]研究占用地图不确定性对全局路径规划的影响, 并提出直接考虑地图不确定性的方法.当若干个障碍物阻塞路径时, 可得到相比确定性规划更可靠的路径, 验证在路径规划过程中关于障碍物不确定存在推理的有用性.由于使用概率占用网格图表示包含噪声的环境, 传统的确定性规划在占用概率上使用硬阈值以声明一个单元是一个障碍, 并相应规划一条路径, 同时将未知空间视为空闲空间.该不确定性规划器规划两个不同的路径假设, 再将它们的初始轨迹段合并为一个以“ 次优视图” 姿态结束的单一轨迹段.随后选择其中一个假设, 或在冲突即将发生时选择一个全新的假设.

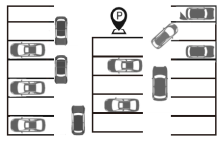
POGM的另一优势是对于结构化环境和非结构化环境都具有良好的表征形式.在拥挤的泊车环境中通常使用占用栅格图表征半结构化环境[102].泊车环境既包含结构化的车位信息, 其行驶策略(前进或倒车)又具有非结构性.在如图13的复杂泊车环境中, 可使用占用栅格图表征车位对不同车辆的“ 吸引力” 系数, 提出一个机会约束优化问题, 最小化扫描区域的成本, 同时满足路径的人流量密度的概率约束[103].

图13 停车场的车辆不确定示意图Fig.13 Vehicles with uncertain intention in parking lot

Souza等[104]提出OEG(Occupancy-Elevation Grid), 表示二维水平栅格上的三维环境, 其中每个单元包含占用概率值、高度及方差, 对应于映射位置.该占用栅格表达使用紧凑的结构表示3D信息, 更适用于处理意外情况和与环境交互.另一种方法是将障碍物储存为栅格图形式并分为四类:非孤立障碍物占据的栅格, 空闲栅格, 仅存在孤立障碍物的栅格, 与上述三类不同但存在于传感器观测的障碍物与自身间连线上的栅格.通过对比连续两帧间栅格的异同, 利用迭代最近点(Iterative Closest Point, IPC)预测其当前障碍物的真实占用概率情况.占用栅格图的优势还包括对于在当前建模下无法规划路径的情况, 可进行二次观测[97].类似于移动智能机器人的优化蚁群算法, 其中信息素浓度的更新可类比于占用栅格图的更新[105].若仍无法得到可行的安全路径, 则从安全脱困的角度规划, 克服陷入局部极小值的情况.

4 不确定性问题研究展望

尽管POMDP与POGM提供解决规划过程中不确定性问题的途径, 但关于不确定性问题的研究仍存在如下两方面的不足.一方面, 不确定性问题因为其自身的高维表示容易陷入维度陷阱, 传统表示方法又难以概括不确定性问题的多样性与通用性.另一方面, 不确定性环境下的规划需要足够鲁棒的模型[106, 107].

规划结构的可靠性不仅取决于安全性, 同时也取决于模型与真实环境的相似程度.与传统的规划方法类似, POMDP和POGM也需要精确的模型对规划进行支持, 但是对于绝大多数场景, POMDP中的奖励函数、状态、观察都是来源于经验或假设.事实上, 这类模型参数具有极大的不确定性.模仿学习、表示学习、多机器人强化学习、时间抽象及贝叶斯强化学习(Bayesian Reinforcement Learning, BRL)等技术可应用于解决模型的不确定性.例如, BRL可将未知参数视为附加的状态变量, 在定义未知参数的先验知识后, 求解最佳收集参数信息的策略[108].因此, 未来的主流解决方法研究集中在学习类方法.

4.1 POMDP与POGM的结合

一个解决不确定性问题的融合性思路是结合POMDP与POGM, 将POGM视为机会约束的一部分.机会约束的增加可以将风险的概念引入不确定性问题.绝大多数规划将重点放在避免碰撞上, 视碰撞为一种机会约束.相比观测的期望, 多数研究者将机会约束表示为概率性的, 使用概率信念相关约束支持风险规避算子, 如CVaR(Conditional Value at Risk)[109].对于绝大多数POMDP问题而言, 表达概率风险规避约束的形式很重要.Zhitnikov等[110]将传统的机会约束POMDP扩展到信念MDP的水平, 并提出PCSS和CCSS, 解决具有挑战性的连续域和可能的非参数设置中的两个公式.

机会约束可通过下述两种方法进行评估:1)假设高斯分布状态变量上的线性约束, 并将机会约束转换为状态均值上的约束, 2)通过蒙特卡洛模拟评估约束.方法2)可处理非高斯分布和非线性约束, 但计算量很大.Aoude等[96]在实验中证实概率约束在避免碰撞方面比传统的机会约束公式更具优势.

POGM通常需要降采样以降低网格节点数, 加快运算速度.但目前的降采样方法往往以随机的形式进行, 可能会忽略关键的环境信息.在未来的研究工作中, 可结合环境属性、降采样、环境预测[111].环境属性包含语义信息、连通情况、总节点数等, 和占用栅格图的抽象性具备一致性.换言之, 当前研究者们致力于将不确定性环境转化为更适合人工智能理解和计算机处理的抽象表征[112].

目前求解方法研究虽然已取得一定进展, 但是大部分还是在处理离散空间, 不适用于处理决策规划问题.对于连续空间且规模较大的问题, 多使用强化学习的方法进行问题求解[113].虽然强化学习缺乏置信度, 难以在真实环境下应用与推广, 但其解决规划决策问题是未来主流的发展趋势, 且从安全性和可靠性上考虑, 未来仍需继续研究.

4.2 多智能体协同

相比规则库和解空间有限的传统规划算法, 研究者更青睐灵活性更高的协同类算法.协同类算法能有效克服单个车辆感知范围有限、在极端情况下难以处理的问题[114].

多智能体决策系统(Multi-agent Decision Sys-tem, MADS)通常是指多个智能体联合起来的决策系统, 系统中的每个智能体都是一个独立决策个体, 通过从环境中获得的信息进行联合决策.这同车联网具有紧密的联系, V2V(Vehicle-to-Vehicle)有助于精确感知现实世界, 快速分析传感数据.每辆车都可对环境独立施以一个动作, 整个系统的状态受到所有车辆联合动作的影响, 因此每辆车的决策过程都需要考虑其它车辆可能采取的动作, 以及这个可能采取的动作对车辆的影响.每辆车单独决策的不确定性包括感知信息延迟、动作执行不完整等.如果加入多车协作, 引入的不确定性会让规划过程变得更复杂.随着车联网技术的发展, V2X(Vehicle to Every-thing)、V2V逐步完善, 对于这种多智能体系统的决策过程, 也可通过DEC-POMDP(Decentralized POM-DP)解决.DEC-POMDP的优势是为多智能体合作任务提供概率框架, 可对结果、环境信息和通信方面不确定性问题进行建模.因为DEC-POMDP利用所有智能体的联合动作, 从一个状态过渡到下一个状态, 可为决策建模提供完整依据.DEC-POMDP的求解方法同POMDP类似, 区别在于将状态、动作、信念和观察均使用联合取代.在任意决策周期内, 系统根据所有车辆的联合动作转移到下一个状态, 同时系统进入下一个决策周期.

DEC-POMDP面临和POMDP同样的问题, 计算量大, 状态描述、策略表达、状态、观测转移的形式都难以确定.相比POMDP随着决策周期指数级增长的运算量, DEC-POMDP面临着双指数级的运算量增加[107].巨大的运算量造成的时间开销已不足以满足自动驾驶安全性的要求, 对于碰撞不能采取及时的制动措施.分组有限空间离线规划算法能在DEC-POMDP中取得较好效果, 从整体上, 算法运行时间也可得到一定降低.但该算法仅适用于小规模的有限空间的问题, 对于大规模DEC-POMDP问题没有帮助[115, 116].

强化学习的引入为求解DEC-POMDP问题提供可能, 但目前基于沟通学习的MARL(Multi-agent Reinforcement Learning)需要假设代理间显式存在信息交互, 该通信往往需要预先进行训练[117].多智能体间的通信需要考虑通信对象选择, 如果要保证所有智能体产生的消息都不被遗漏, 就可能会引入许多无用的信息, 影响通信效率, 增大通信成本.特别是对于拥挤路口, 智能体数量较多, 不确定性较高, 对于这些冗余信息的处理容易导致不安全的导航结果.分层通信和将通信对象的选择视为任务的端到端方法可提升通信效果.基于协作学习的MARL结合多智能体学习的思想与强化学习, 通常可分为基于值的方法[117]和Actor-Critic网络[118].前者对于较复杂的环境, 无法较好地处理非平稳环境, 后者通过中心化学习评论家, 在较好处理算法可扩展性问题的同时, 拥有较好的抗环境非平稳能力.

除了多智能体的协同强化学习, 协同模仿学习也获得研究者的青睐.协同模仿学习有利于提升单独车辆的感知能力.COOPERNAUT[119]利用跨车辆感知进行基于视觉的协作驾驶, 共享车联网中的全部车辆获取的感知信息.协同驾驶可扩大主体车辆的感知范围, 并传递其它车辆的意图和路径规划结果, 有助于在事故频发时给出安全的可行路径.模仿学习能通过大量数据, 端到端地实现从感知输入到直接输出规划结果.这种学习形式更符合人类思维, 有利于在不确定性环境中实现类人驾驶.对于模仿学习而言, 完全信赖专家系统, 高度依赖数据集的规模与质量.模仿学习仅学习可行策略, 对不可行策略没有试错过程, 缺乏在极端环境下的处理能力[120, 121].因此, 随着大数据的应用与分布式运算等计算方法的发展, 将场景内全部车辆的感知信息作为单车传感增强, 学习协作感知的自动驾驶策略, 可在结构化环境与非结构化环境下均获得较优的导航效果.

对于多智能体系统, 不仅需要考虑协作, 也需要考虑对抗.随着网联汽车发展, 必须考虑保护性的对抗行为.系统内对抗恶意个体产生的对抗或许不享有共同的奖励, 同样会引入不确定性, 这对车联网中隐私安全保护提出更高要求.

4.3 面临的挑战

传统的规划方法对于不确定性问题的研究十分匮乏.主流的POMDP面临建模不够准确、计算耗时、不满足规划实时性的问题.概率占用图对于感知的不确定性具有较好的处理能力, 但是难以解决误检问题.基于栅格图的部分规划算法可能会导致车辆受困:蚁群算法在局部极小值点上不能采取下一步行动; 人工势场方法落入斥力与引力相等的节点, 都难以得到未来路径.学习类的方法难以推行的一大阻碍是信任问题.事实上, 自动驾驶是不容错的人工智能系统, 无论是数据获取过程, 还是实验测试过程, 都难以在真正的车辆行驶环境下进行.不确定性会增大真实环境与虚拟环境的区别, 降低驾驶员对自动驾驶决策的信任水平.

本文展望两种未来解决规划决策问题的方法, 可有效克服上述缺陷, 加快规划速度, 提升对周围环境的感知能力.但结合POMDP和POGM的方法得出的结果通常是离散的加速度域和速度域.不确定性问题求解的有限解空间难以涵盖所有情况, 可能因为速度离散而导致在真实情况下可行的速度矢量在解空间之外.虽然多智能体协同的方法虽然能通过共享目标和状态, 增大感知视野进行多智能体系统的规划, 但其运算量较大, 收敛到良好解的速度较慢, 并且假设智能体总开始于零知识状态.目前自动驾驶技术通常需要结合专家建议, 但是对于数据集的质量和规模要求较高.协同学习依赖车联网间的通信, 对通信技术要求较高, 往往只能解决缓慢变化的环境.

尽管目前自动驾驶还面临许多方面的问题, 但人工智能技术将持续全面融合认知科学、心理学、生物学、社会学等多学科, 推动自动驾驶应用与发展.研究者希望能在不确定性环境下的规划问题中具有更好的建模与求解方法, 为自动驾驶的发展提供可能.

5 结束语

本文介绍不确定性环境下自动驾驶的规划过程.首先介绍不确定性问题的表示, 并介绍解决该问题的必要性与难点, 从理论基础、求解方法及具体应用三方面介绍两种主流的解决规划过程中的不确定性问题的方法.最后深入分析当下该领域的发展现状与面临的挑战, 针对高效性、可靠性、交互性等多方面对未来的研究方向进行展望.纵览近年自动驾驶的成果可看出, 自动驾驶正朝向类人、可靠、智能的方向发展.不确定性问题是自动驾驶发展必须克服的一道难关, 应从定位、感知、地图、规划、控制各环节应对这种不确定性, 共同构成安全可靠、应用场景广泛的自动驾驶系统.

本文责任编委 吴 飞

Recommended by Associate Editor WU Fei

参考文献
[1] THRUN S, MONTEMERLO M, DAHLKAMP H, et al. Stanley: The Robot That Won the DARPA Grand Challenge // BUEHLER M, IAGNEMNA K, SINGH S, eds. The 2005 DARPA Grand Cha-llenge. Berlin, Germany: Springer, 2007: 1-43. [本文引用:1]
[2] 秦志嫒, 白文岭, 贾宁. 智能网联汽车企业技术路径解析. 汽车与配件, 2019(9): 31-33.
(QIN Z Y, BAI W L, JIA N. Analysis of Technical Path of Intelli-gent Networked Vehicle Enterprises. Automobile and Parts, 2019(9): 31-33. ) [本文引用:1]
[3] PALMEIRO A R, VAN DER KINT S, VISSERS L, et al. Interaction between Pedestrians and Automated Vehicles: A Wizard of Oz Experiment. Transportation Research Part F(Traffic Psychology and Behaviour), 2018, 58: 1005-1020. [本文引用:1]
[4] JUN M, CHAUDHRY A I, ANDREA R D. The Navigation of Autonomous Vehicles in Uncertain Dynamic Environments: A Case Study // Proc of the 41st IEEE Conference on Decision and Control. Washington, USA: IEEE, 2002: 3770-3775. [本文引用:1]
[5] KIBALOV V, SHIPITKO O. Safe Speed Control and Collision Pro-bability Estimation Under Ego-Pose Uncertainty for Autonomous Vehicle // Proc of the 23rd IEEE International Conference on Intelligent Transportation Systems. Washington, USA: IEEE, 2020. DOI: 10.1109/ITSC.45102.2020.9294531. [本文引用:1]
[6] BERNSTEIN D S, GIVAN R, IMMERMAN N, et al. The Comple-xity of Decentralized Control of Markov Decision Processes. Mathematics of Operations Research, 2002, 27(4): 819-840. [本文引用:1]
[7] 房俊恒. 基于点的值迭代算法在POMDP问题中的研究. 硕士学位论文. 苏州: 苏州大学, 2015.
(FANG J H. Research on Point-Based Value Iteration Algorithm in POMDP Domains. Master Dissertation. Suzhou, China: Soochow University, 2015. ) [本文引用:1]
[8] PINEAU J, GORDON G, THRUN S. Point-Based Value Iteration: An Anytime Algorithm for POMDPs // Proc of the 18th International Joint Conference on Artificial Intelligence. San Francisco, USA: Morgan Kaufmann, 2003: 1025-1030. [本文引用:2]
[9] BAI H Y, CAI S J, YE N, et al. Intention-Aware Online POMDP Planning for Autonomous Driving in a Crowd // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2015: 454-460. [本文引用:3]
[10] LUO Y F, CAI P P, BERA A, et al. PORCA: Modeling and Planning for Autonomous Driving Among Many Pedestrians. IEEE Robotics and Automation Letters, 2018, 3(4): 3418-3425. [本文引用:2]
[11] CAI P P, LUO Y F, SAXENA A, et al. LeTS-Drive: Driving in a Crowd by Learning from Tree Search[C/OL]. [2022-11-16]. https://arxiv.org/pdf/1905.12197.pdf. [本文引用:2]
[12] MONAHAN G E. State of the Art-A Survey of Partially Observable Markov Decision Processes: Theory, Models, and Algorithms. Management Science, 1982, 28(1): 1-16. [本文引用:1]
[13] JORRITSMA P H M. Incremental Region Enhanced Neural Q-Learning for Solving Model-Based POMDPs. Bachelor Dissertation. Groningen, The Netherland s: University of Groningen, 2011. [本文引用:1]
[14] HORÁK K, BOŠANSKý B, CHATTERJEE K. Goal-HSVI: Heuristic Search Value Iteration for Goal-POMDPs // Proc of the 27th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2018: 4764-4770. [本文引用:1]
[15] 杜波. 启发式概率值迭代算法: 一种求解POMDP问题的近似框架. 硕士学位论文. 南京: 南京大学, 2014.
(DU B. Heuristic Probabilistic Value Iteration: An Approximation Framework for POMDPs. Master Dissertation. Nanjing, China: Nanjing University, 2014. ) [本文引用:1]
[16] 孙湧, 仵博, 冯延蓬. 基于策略迭代和值迭代的POMDP算法. 计算机研究与发展, 2008, 45(10): 1763-1768.
(SUN Y, WU B, FENG Y P. A Policy- and Value- Iteration Algorithm for POMDP. Journal of Computer Research and Development, 2008, 45(10): 1763-1768. ) [本文引用:1]
[17] CHEN Y C, KOCHENDERFER M J, SPAAN M T J. Improving Offline Value-Function Approximations for POMDPs by Reducing Discount Factors // Proc of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington, USA: IEEE, 2018: 3531-3536. [本文引用:1]
[18] THRUN S. Monte Carlo POMDPs // Proc of the 12th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 1999: 1064-1070. [本文引用:1]
[19] SILVER D, VENESS J. Monte-Carlo Planning in Large POMDPs // Proc of the 23rd International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2010, II: 2164-2172. [本文引用:1]
[20] NYLUND K L, ASPAROUHOV T, MUTHÉN B O. Deciding on the Number of Classes in Latent Class Analysis and Growth Mixture Modeling: A Monte Carlo Simulation Study. Structural Equation Modeling: A Multidisciplinary Journal, 2007, 14(4): 535-569. [本文引用:1]
[21] 郑红燕, 仵博, 冯延蓬, 等. 基于信念点裁剪策略树的POMDP求解算法. 信息与控制, 2013, 42(1): 53-57.
(ZHENG H Y, WU B, FENG Y P, et al. Belief Point-Based POMDP Solution for Policy Tree Pruning. Information and Control, 2013, 42(1): 53-57. ) [本文引用:1]
[22] WOLF T B, KOCHENDERFER M J. Aircraft Collision Avoidance Using Monte Carlo Real-Time Belief Space Search. Journal of Intelligent and Robotic Systems, 2011, 64: 277-298. [本文引用:1]
[23] 章宗长, 陈小平. 杂合启发式在线POMDP规划. 软件学报, 2013, 24(7): 1589-1600.
(ZHANG Z C, CHEN X P. Hybrid Heuristic Online Planning for POMDPs. Journal of Software, 2013, 24(7): 1589-1600. ) [本文引用:1]
[24] ZHANG Z Z, HSU D, LEE W S. Covering Number for Efficient Heuristic-Based POMDP Planning // Proc of the 31st International Conference on Machine Learning. San Diego, USA: JMLR, 2014: 28-36. [本文引用:1]
[25] 石轲. 基于马尔可夫决策过程理论的Agent决策问题研究. 硕士学位论文. 合肥: 中国科学技术大学, 2010.
(SHI K. Research on Agent Decision Problem Based on Markov Decision Process Theory. Master Dissertation. Hefei, China: University of Science and Technology of China, 2010. ) [本文引用:1]
[26] KARKUS P, HSU D, LEE W S. QMDP-Net: Deep Learning for Planning under Partial Observability // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 4697-4707. [本文引用:1]
[27] YUN C, CHOI S. Visual Localization and POMDP for Autonomous Indoor Navigation[J/OL]. [2022-11-16]. https://documents.pub/document/visual-localization-and-pomdp-for-autonomous-indoor-.html. [本文引用:1]
[28] VLASSIS N, LITTMAN M L, BARBER D. On the Computational Complexity of Stochastic Controller Optimization in POMDPs. ACM Transactions on Computation Theory, 2012, 4(4). DOI: 10.1145/2382559.2382563. [本文引用:1]
[29] TUTTLE E, GHAHRAMANI Z. Propagating Uncertainty in POMDP Value Iteration with Gaussian Processes[C/OL]. [2022-11-16]. https://citeseerx.ist.psu.edu/doc/10.1.1.400.6737. [本文引用:1]
[30] WASHINGTON R. BI-POMDP: Bounded, Incremental, Partially-Observable Markov-Model Planning // Proc of the European Conference on Planning. Berlin, Germany: Springer, 1997: 440-451. [本文引用:1]
[31] ROSS S, PINEAU J, CHAIB-DRAA B. Online Policy Improvement in Large POMDPs via an Error Minimization Search[C/OL]. [2022-11-16]. https://www.cs.cmu.edu/~sross1/publications/Ross-NESCAI07-AEMS.pdf. [本文引用:1]
[32] YE N, SOMANI A, HSU D, et al. DESPOT: Online POMDP Planning with Regularization. Journal of Artificial Intelligence Research, 2017, 58(1): 231-266. [本文引用:1]
[33] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Playing Atari with Deep Reinforcement Learning[C/OL]. [2022-11-16]. https://arxiv.org/pdf/1312.5602.pdf. [本文引用:1]
[34] WANG Z Y, SCHAUL T, HESSEL M, et al. Dueling Network Architectures for Deep Reinforcement Learning // Proc of the 33rd International Conference on Machine Learning. San Diego, USA: JMLR, 2016: 1995-2003. [本文引用:1]
[35] VAN HASSELT V, GUEZ A, SILVER D. Deep Reinforcement Learning with Double Q-Learning. Proceedings of the AAAI Conference on Artificial Intelligence, 2016, 30(1): 2094-2100. [本文引用:1]
[36] HESSEL M, MODAYIL J, VAN HASSELT H, et al. Rainbow: Combining Improvements in Deep Reinforcement Learning // Proc of the 32nd AAAI Conference on Artificial Intelligence and 30th Innovative Applications of Artificial Intelligence Conference and 8th AAAI Symposium on Educational Advances in Artificial Intelligence. Palo Alto, USA: AAAI, 2018: 3215-3222. [本文引用:1]
[37] HAARNOJA T, ZHOU A, HARTIKAINEN K, et al. Soft Actor-Critic Algorithms and Applications[C/OL]. [2022-11-16]. https://arxiv.org/pdf/1812.05905.pdf. [本文引用:1]
[38] LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous Control with Deep Reinforcement Learning[C/OL]. [2022-11-16]. https://arxiv.org/pdf/1509.02971.pdf. [本文引用:1]
[39] EGOROV M Deep Reinforcement Learning with POMDPs[C/OL]. [2022-11-16]. http://cs229.stanford.edu/proj2015/363_report.pdf. [本文引用:1]
[40] HAUSKNECHT M, STONE P. Deep Recurrent Q-Learning for Partially Observable MDPs[C/OL]. [2022-11-16]. https://arxiv.org/pdf/1507.06527.pdf. [本文引用:1]
[41] HOCHREITER S, SCHMIDHUBER J. Long Short-Term Memory. Neural Computation, 1997, 9(8): 1735-1780. [本文引用:1]
[42] FOERSTER J N, ASSAEL Y M, DE FREITAS N, et al. Learning to Communicate to Solve Riddles with Deep Distributed Recurrent Q-Networks[C/OL]. [2022-11-16]. https://arxiv.org/pdf/1602.02672.pdf. [本文引用:1]
[43] ZHU P F, LI X, POUPART P, et al. On Improving Deep Rein-forcement Learning for POMDPs[C/OL]. [2022-11-16]. https://arxiv.org/pdf/1704.07978.pdf. [本文引用:1]
[44] IGL M, ZINTGRAF L, LE T A, et al. Deep Variational Reinforcement Learning for POMDPs. Proceedings of Machine Learning Research, 2018, 80: 2117-2126. [本文引用:1]
[45] LE T A, IGL M, RAINFORTH T, et al. Auto-Encoding Sequential Monte Carlo[C/OL]. [2022-11-16]. https://arxiv.org/pdf/1705.10306.pdf. [本文引用:1]
[46] WANG Y B, LIU B, WU J J, et al. DualSMC: Tunneling Diffe-rentiable Filtering and Planning under Continuous POMDPs // Proc of the 29th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2020: 4190-4198. [本文引用:1]
[47] SINGH G, PERI S, KIM J, et al. Structured World Belief for Reinforcement Learning in POMDP. Proceedings of Machine Learning Research, 2021, 139: 9744-9755. [本文引用:1]
[48] CHEN X Y, MU Y M, LUO P, et al. Flow-Based Recurrent Belief State Learning for POMDPs. Proceedings of Machine Learning Research, 2022, 162: 3444-3468. [本文引用:1]
[49] DINH L, SOHL-DICKSTEIN J, BENGIO S. Density Estimation Using Real NVP[C/OL]. [2022-11-16]. https://arxiv.org/pdf/1605.08803.pdf. [本文引用:1]
[50] TASSA Y, DORON Y, MULDAL A, et al. DeepMind Control Suite[C/OL]. [2022-11-16]. https://arxiv.org/pdf/1801.00690.pdf. [本文引用:1]
[51] FERRER G, GARRELL A, SANFELIU A. Robot Companion: A Social-Force Based Approach with Human Awareness-Navigation in Crowded Environments // Proc of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington, USA: IEEE, 2014: 1688-1694. [本文引用:1]
[52] LÖHNER R. On the Modeling of Pedestrian Motion. Applied Ma-thematical Modelling, 2010, 34(2): 366-382. [本文引用:1]
[53] HELBING D, MOLNÁR P. Social Force Model for Pedestrian Dynamics. Physical Review E, 1995, 51(5): 4282-4286. [本文引用:1]
[54] SEDIGHI S, VAN NGUYEN D, KUHNERT K D. Guided Hybrid A-Star Path Planning Algorithm for Valet Parking Applications // Proc of the 5th International Conference on Control, Automation and Robotics. Washington, USA: IEEE, 2019: 570-575. [本文引用:1]
[55] CONLTER R C. Implementation of the Pure Pursuit Path Tracking Algorithm. Technical Report, CMU-RI-TR-92-01. Pittsburgh, USA: Carnegie Mellon University, 1992. [本文引用:1]
[56] CAI P P, LUO Y F, HSU D, et al. HyP-DESPOT: A Hybrid Pa-rallel Algorithm for Online Planning Under Uncertainty[C/OL]. [2022-11-16]. https://arxiv.org/pdf/1802.06215v1.pdf. [本文引用:1]
[57] BOUTON M, COSGUN A, KOCHENDERFER M J. Belief State Planning for Autonomously Navigating Urban Intersections // Proc of the IEEE Intelligent Vehicles Symposium. Washington, USA: IEEE, 2017: 825-830. [本文引用:2]
[58] LIN X, ZHANG J C, SHANG J, et al. Decision Making Through Occluded Intersections for Autonomous Driving // Proc of the IEEE Intelligent Transportation Systems Conference. Washington, USA: IEEE, 2019: 2449-2455. [本文引用:1]
[59] HUBMANN C, QUETSCHLICH N, SCHULZ J, et al. A POMDP Maneuver Planner for Occlusions in Urban Scenarios // Proc of the IEEE Intelligent Vehicles Symposium. Washington, USA: IEEE, 2019: 2172-2179. [本文引用:1]
[60] PRUEKPRASERT S, ZHANG X Y, DUBUT J, et al. Decision Making for Autonomous Vehicles at Unsignalized Intersection in Presence of Malicious Vehicles // Proc of the IEEE Intelligent Transportation Systems Conference. Washington, USA: IEEE, 2019: 2299-2304. [本文引用:1]
[61] MEGHJANI M, LUO Y F, HO Q H, et al. Context and Intention Aware Planning for Urban Driving // Proc of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington, USA: IEEE, 2019: 2891-2898. [本文引用:1]
[62] ULBRICH S, MAURER M. Probabilistic Online POMDP Decision Making for Lane Changes in Fully Automated Driving // Proc of the 16th International IEEE Conference on Intelligent Transportation Systems. Washington, USA: IEEE, 2013: 2063-2070. [本文引用:1]
[63] MENTASTI S, MATTEUCCI M. Multi-layer Occupancy Grid Ma-pping for Autonomous Vehicles Navigation // Proc of the AEIT International Conference of Electrical and Electronic Technologies for Automotive. Washington, USA: IEEE, 2019. DOI: 10.23919/EETA.2019.8804556. [本文引用:1]
[64] KHONJI M, JASOUR A, WILLIAMS B C. Approximability of Constant-Horizon Constrained POMDP // Proc of the 28th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2019: 5583-5590. [本文引用:1]
[65] DING W C, ZHANG L, CHEN J, et al. Safe Trajectory Generation for Complex Urban Environments Using Spatio-Temporal Se-mantic Corridor. IEEE Robotics and Automation Letters, 2019, 4(3): 2997-3004. [本文引用:1]
[66] CHEN X Y L, LI S J, MERSCH B, et al. Moving Object Segmentation in 3D LiDAR Data: A Learning-Based Approach Exploiting Sequential Data. IEEE Robotics and Automation Letters, 2021, 6(4): 6529-6536. [本文引用:1]
[67] LAGHMARA H, BOUDALI M T, LAURAIN T, et al. Obstacle Avoidance, Path Planning and Control for Autonomous Vehicles // Proc of the IEEE Intelligent Vehicles Symposium. Washington, USA: IEEE, 2019: 529-534. [本文引用:1]
[68] YANG Z C, GAO Z H, GAO F, et al. Lane Changing Assistance Strategy Based on an Improved Probabilistic Model of Dynamic Occu-pancy Grids. Frontiers of Information Technology and Electronic Engineering, 2021, 22(11): 1492-1504. [本文引用:2]
[69] ELFES A. Using Occupancy Grids for Mobile Robot Perception and Navigation. Computer, 1989, 22(6): 46-57. [本文引用:1]
[70] MERHY B A, PAYEUR P, PETRIU E M. Application of Segmented 2-D Probabilistic Occupancy Maps for Robot Sensing and Navigation. IEEE Transactions on Instrumentation and Measurement, 2008, 57(12): 2827-2837. [本文引用:1]
[71] TSARDOULIAS E G, ILIAKOPOULOU A, KARGAKOS A, et al. A Review of Global Path Planning Methods for Occupancy Grid Maps Regardless of Obstacle Density. Journal of Intelligent and Robotic Systems, 2016, 84(1/2/3/4): 829-858. [本文引用:1]
[72] YANG K, GAN S K, HUH J, et al. Optimal Spline-Based RRT Path Planning Using Probabilistic Map // Proc of the 14th International Conference on Control, Automation and Systems. Washington, USA: IEEE, 2014: 643-646. [本文引用:2]
[73] PENDLETON S D, LIU W, ANDERSEN H, et al. Numerical Approach to Reachability-Guided Sampling-Based Motion Planning Under Differential Constraints. IEEE Robotics and Automation Letters, 2017, 2(3): 1232-1239. [本文引用:1]
[74] KARAMAN S, WALTER M R, PEREZ A, et al. Anytime Motion Planning Using the RRT* // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2011: 1478-1483. [本文引用:1]
[75] FULGENZI C, SPALANZANI A, LAUGIER C, et al. Risk Based Motion Planning and Navigation in Uncertain Dynamic Environment[C/OL]. [2022-11-20]. https://hal.inria.fr/inria-00526601/file/PPRRT.pdf. [本文引用:1]
[76] MA H, MENG F, YE C W, et al. Bi-Risk-RRT Based Efficient Motion Planning for Autonomous Ground Vehicles. IEEE Transactions on Intelligent Vehicles, 2022, 7(3): 722-733. [本文引用:1]
[77] YANG H X, XU X M, HONG J C. Automatic Parking Path Pla-nning of Tracked Vehicle Based on Improved A* and DWA Algorithms. IEEE Transactions on Transportation Electrification, 2022. DOI: 10.1109/TTE.2022.3199255. [本文引用:1]
[78] PAN Z C, YUAN M X, WANG R H, et al. D2WA: “Dynamic” DWA for Motion Planning of Mobile Robots in Dynamic Environments. International Journal of Dynamics and Control, 2022. DOI: 10.1007/s40435-022-01092-3. [本文引用:1]
[79] KOENIG S, LIKHACHEV M, FURCY D. Lifelong Planning A*. Artificial Intelligence, 2004, 155(1/2): 93-146. [本文引用:1]
[80] STENTZ A. Optimal and Efficient Path Planning for Partially Known Environments // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 1994: 3310-3317. [本文引用:1]
[81] YANG L, QI J T, SONG D L, et al. Survey of Robot 3D Path Planning Algorithms. Journal of Control Science and Engineering, 2016. DOI: 10.1155/2016/7426913. [本文引用:2]
[82] KIM D, KWON Y, YOON S E. Dancing PRM*: Simultaneous Planning of Sampling and Optimization with Configuration Free Space Approximation // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2018: 7071-7078. [本文引用:1]
[83] WANG Y J, LIU Z X, ZUO Z Q, et al. Trajectory Planning and Safety Assessment of Autonomous Vehicles Based on Motion Prediction and Model Predictive Control. IEEE Transactions on Vehi-cular Technology, 2019, 68(9): 8546-8556. [本文引用:1]
[84] SAROYA M, BEST G, HOLLINGER G A. Roadmap Learning for Probabilistic Occupancy Maps with Topology-Informed Growing Neural Gas. IEEE Robotics and Automation Letters, 2021, 6(3): 4805-4812. [本文引用:1]
[85] OK K, ANSARI S, GALLAGHER B, et al. Path Planning with Uncertainty: Voronoi Uncertainty Fields // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2013: 4596-4601. [本文引用:1]
[86] MCLEOD S, XIAO J. Navigating Dynamically Unknown Environments Leveraging Past Experience // Proc of the International Conference on Robotics and Automation. Washington, USA: IEEE, 2019: 29-35. [本文引用:4]
[87] JIMÉNEZ V, GODOY J, ARTUÑEDO A, et al. Object-Wise Com-parison of LiDAR Occupancy Grid Scan Rendering Methods. Robotics and Autonomous Systems, 2023, 161. DOI: 10.1016/j.robot.2023.104363. [本文引用:1]
[88] SUN N, FAN Z Q, QIU Q, et al. Map Construction Fusing Environmental Information and Motion Constraints // Proc of the Chinese Intelligent Automation Conference. Berlin, Germany: Springer, 2021: 637-644. [本文引用:1]
[89] ELHAFSI A, IVANOVIC B, JANSON L, et al. Map-Predictive Motion Planning in Unknown Environments // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2020: 8552-8558. [本文引用:1]
[90] BUI H D, LU Y J, PLAKU E. Improving the Efficiency of Sampling-Based Motion Planners via Runtime Predictions for Motion-Planning Problems with Dynamics // Proc of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington, USA: IEEE, 2022: 4486-4491. [本文引用:1]
[91] JUNG Y, SEO S W, KIM S W. Fast Point Clouds Upsampling with Uncertainty Quantification for Autonomous Vehicles // Proc of the International Conference on Robotics and Automation. Washington, USA: IEEE, 2022: 7776-7782. [本文引用:1]
[92] WANG L Z, YE H K, WANG Q H, et al. Learning-Based 3D Occupancy Prediction for Autonomous Navigation in Occluded Environments // Proc of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington, USA: IEEE, 2021: 4509-4516. [本文引用:1]
[93] DU TOIT N E, BURDICK J W. Probabilistic Collision Checking With Chance Constraints. IEEE Transactions on Robotics, 2011, 27(4): 809-815. [本文引用:1]
[94] ZHU H, ALONSO-MORA J. Chance-Constrained Collision Avoidance for MAVs in Dynamic Environments. IEEE Robotics and Automation Letters, 2019, 4(2): 776-783. [本文引用:1]
[95] DADKHAH N, METTLER B. Survey of Motion Planning Literature in the Presence of Uncertainty: Considerations for UAV Guidance. Journal of Intelligent and Robotic Systems, 2012, 65: 233-246. [本文引用:1]
[96] AOUDE G S, LUDERS B D, JOSEPH J M, et al. Probabilistically Safe Motion Planning to Avoid Dynamic Obstacles with Uncertain Motion Patterns. Autonomous Robots, 2013, 35: 51-76. [本文引用:2]
[97] SODHI P, HO B J, KAESS M. Online and Consistent Occupancy Grid Mapping for Planning in Unknown Environments // Proc of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington, USA: IEEE, 2019: 7879-7886. [本文引用:2]
[98] ARTUÑEDO A, VILLAGRA J, GODOY J, et al . Motion Planning Approach Considering Localization Uncertainty. IEEE Transactions on Vehicular Technology, 2020, 69(6): 5983-5994. [本文引用:1]
[99] LAU B, SPRUNK C, BURGARD W. Efficient Grid-Based Spatial Representations for Robot Navigation in Dynamic Environments. Robotics and Autonomous Systems, 2013, 61(10): 1116-1130. [本文引用:1]
[100] LÜZOW L, MENG Y, ARMIJOS A C, et al. Density Planner: Minimizing Collision Risk in Motion Planning with Dynamic Obstacles Using Density-Based Reachability[C/OL]. [2022-11-16]. https://arxiv.org/pdf/2210.02131.pdf. [本文引用:1]
[101] BANFI J, WOO L, CAMPBELL M. Is It Worth to Reason About Uncertainty in Occupancy Grid Maps During Path Planning? // Proc of the International Conference on Robotics and Automation. Washington, USA: IEEE, 2022: 11102-11108. [本文引用:1]
[102] CHOHAN N, NAZARI M A, WYMEERSCH H, et al. Robust Trajectory Planning of Autonomous Vehicles at Intersections with Communication Impairments // Proc of the 57th Annual Allerton Conference on Communication, Control, and Computing. Washington, USA: IEEE, 2019: 832-839. [本文引用:1]
[103] JABR B A, AGGARWAL R, KUMAR M. Optimal Allocation of Autonomous Vehicles Using Chance-Constraints for Mapping a Semi-Structured Environment // Proc of the AIAA SCITECH Forum. Reston, USA: AIAA, 2022. DOI: 10.2514/6.2022-1413. [本文引用:1]
[104] SOUZA A, MAIA R S, AROCA R V, et al. Probabilistic Robotic Grid Mapping Based on Occupancy and Elevation Information // Proc of the 16th International Conference on Advanced Robotics. Washington, USA: IEEE, 2013. DOI: 10.1109/ICAR/2013.6766467 [本文引用:1]
[105] BRAND M, MASUDA M, WEHNER N, et al. Ant Colony Optimization Algorithm for Robot Path Planning // Proc of the Inter-national Conference on Computer Design and Applications. Washing-ton, USA: IEEE, 2010: V3-436-V3-440. [本文引用:1]
[106] PUSSE F, KLUSCH M. Hybrid Online POMDP Planning and Deep Reinforcement Learning for Safer Self-Driving Cars // Proc of the IEEE Intelligent Vehicles Symposium. Washington, USA: IEEE, 2019: 1013-1020. [本文引用:1]
[107] 章宗长. 部分可观察马氏决策过程的复杂性理论及规划算法研究. 博士学位论文. 合肥: 中国科学技术大学, 2012.
(ZHANG Z C. Complexity Theory and Planning Algorithms in Partially Observable Markov Decision Processes. Ph. D. Dissertation. Hefei, China: University of Science and Technology of China, 2012. ) [本文引用:2]
[108] 郑建阳. 无先验知识的部分可观测环境规划问题研究. 硕士学位论文. 厦门: 厦门大学, 2019.
(ZHENG J Y. Research on Planning in Partially Observable Domains without Prior Knowledge. Master Dissertation. Xiamen, China: Xiamen University, 2019. ) [本文引用:1]
[109] BARBOSA F S, LACERDA B, DUCKWORTH P, et al. Risk-Aware Motion Planning in Partially Known Environments // Proc of the 60th IEEE Conference on Decision and Control. Washington, USA: IEEE, 2021: 5220-5226. [本文引用:1]
[110] ZHITNIKOV A, INDELMAN V. Risk Aware Belief-Dependent Constrained POMDP Planning[C/OL]. [2022-11-16]. https://arxiv.org/pdf/2209.02679v1.pdf. [本文引用:1]
[111] LEE K, KUM D. Collision Avoidance/Mitigation System: Motion Planning of Autonomous Vehicle via Predictive Occupancy Map. IEEE Access, 2019, 7: 52846-52857. [本文引用:1]
[112] FISHER A, CANNIZZARO R, COCHRANE M, et al. ColMap: A Memory-Efficient Occupancy Grid Mapping Framework. Robo-tics and Autonomous Systems, 2021, 142. DOI: 10.1016/j.robot.2021.103755. [本文引用:1]
[113] MARBLE J D, BEKRIS K E. Asymptotically Near-Optimal Pla-nning with Probabilistic Roadmap Spanners. IEEE Transactions on Robotics, 2013, 29(2): 432-444. [本文引用:1]
[114] 郭靖. 基于马氏决策理论的智能体决策问题研究. 硕士学位论文. 广州: 广东工业大学, 2012.
(GUO J. Research on Agent Decision Issues Problem Based on Markov Decision Theory. Master Dissertation. Guangzhou, China: Guangdong University of Technology, 2012. ) [本文引用:1]
[115] SCHEFTELOWITSCH D. The Complexity of Uncertainty in Mar-kov Decision Processes // Proc of the SIAM Conference on Control and Its Applications. Philadelphia, USA: SIAM, 2015: 303-310. [本文引用:1]
[116] DOYEN L, MASSART T, SHIRMOHAMMADI M. The Complexity of Synchronizing Markov Decision Processes. Journal of Computer and System Sciences, 2019, 100: 96-129. [本文引用:1]
[117] LEE H R, LEE T. Multi-agent Reinforcement Learning Algorithm to Solve a Partially-Observable Multi-agent Problem in Disaster Response. European Journal of Operational Research, 2021, 291(1): 296-308. [本文引用:2]
[118] THOMAS J, HERNÁNDEZ M P, PARLIKAD A K, et al. Network Maintenance Planning via Multi-agent Reinforcement Lear-ning // Proc of the IEEE International Conference on Systems, Man, and Cybernetics. Washington, USA: IEEE, 2021: 2289-2295. [本文引用:1]
[119] CUI J X, QIU H, CHEN D, et al. COOPERNAUT: End-to-End Driving with Cooperative Perception for Networked Vehicles // Proc of the IEEE/CVF Conference on Computer Vision and Pa-ttern Recognition. Washington, USA: IEEE, 2022: 17231-17241. [本文引用:1]
[120] AITTAHAR S, FRANÇOIS-LAVET V, LODEWEYCKX S, et al. Imitative Learning for Online Planning in Microgrids // Proc of the International Workshop on Data Analytics for Renewable Energy Integration. Berlin, Germany: Springer, 2015: 1-15. [本文引用:1]
[121] TIGAS P, FILOS A, MCALLISTER R, et al. Robust Imitative Planning: Planning from Demonstrations Under Uncertainty[C/OL]. [2022-11-16]. http://neurips.wad.vision/files/papers/Robust%20Imitative%20Planning:%20Planning%20from%20Demonstrations%20Under%20Uncertainty.pdf. [本文引用:1]