深度图中每个像素点值的大小表示该点与相机的距离, 因此, 在深度图中不同运动层对应的深度值存在明显的区别, 可以为场景流计算提供重要的边界轮廓信息和结构信息.在基于RGBD图像序列场景流计算中, 通常利用深度图中的空间信息将图像场景划分至不同的层, 再对应估计每层的运动.但是, 这种场景分层方法仅利用图像中的静态信息条件以确定图像的区域分割, 既不充分也不可靠.

深度图空间信息分层结果如图1所示.由图可以看出, 仅利用深度信息分层虽然在一定程度上可以获得较好的场景分层分割结果, 但是在(c)蓝色方框所示区域, 也存在将应划分为同一层的区域误分配至不同层的误分层问题.究其原因, 主要是受到深度图中噪声等异常值因素的干扰.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 深度图空间信息分层结果Fig.1 Spatial information layering result of depth image

由图2可以看出, 深度图由于受噪声的影响, 没有很好地对齐边界与图像平面中的对象边界, 因此造成深度分层结果不够准确.但深度图中包含的空间层次信息仍然可以为场景的分层提供足够的指导, 这也是基于RGBD图像序列场景计算方法的基础.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 噪声等异常值在深度图与RGB图像对齐中的影响Fig.2 Effect of noise and other outliers on alignment of depth image and RGB image

为此, 相关研究试图通过寻求其它额外的附加约束以提高深度图深度分层结果的准确性.例如:设计深度加权函数, 避免深度分层的不连续性^[23]或引入场景分割约束, 降低深度分层结果的误差^[24].本文关注到利用场景中物体的运动信息可以更好地优化深度图深度分层, 因此, 针对深度分层结果准确性与可靠性不足的问题, 本文提出基于高斯混合模型的光流聚类分割模型, 从光流中提取目标运动信息, 增强场景目标之间的运动联系, 并逐层优化深度图分层分割结果, 有效缓解深度空间信息场景分层分割产生的错误划分问题, 进而为后续RGBD场景流计算提供高置信度的深度运动分层分割结果.

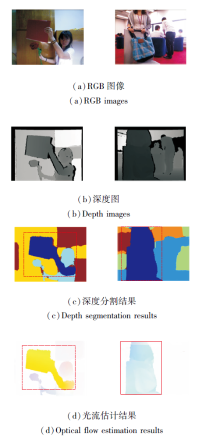
光流主要用于捕获场景中运动目标的层次信息, 深度分层是利用静态的空间距离信息实现场景层次分割.虽然二者在分割依据方面存在差异, 但是对场景层次的划分存在一定相似性.不同场景光流估计结果与深度分层结果在主要运动区域的层次相似性如图3所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同场景光流估计结果与深度分层结果在主要运动区域的层次相似性Fig.3 Hierarchy similarity of optical flow estimation results and depth laying results in different scenes in main motion regions

由图3可以看出, 尽管相比光流结果, 深度分层结果呈现出更多的层次, 但是它们在主要运动区域的层次划分是相似的, 如(d)中标签区域.本文模型主要利用捕获的运动信息优化静态的距离分层, 因此, 只需光流估计结果与深度分层结果在主要的运动目标物体上分层相似便可满足要求.同时通过大量实验分析验证, 这种相似性在大多数场景均可以得到满足.

基于深度分层与光流结果间具有的相似性, 本文首先假设图像场景的运动是呈现局部刚性的.一方面, 因为具有一致局部刚性运动的区域通常在运动过程中不易发生形变, 另一方面, 局部刚性运动区域的运动形式一般趋于一致.然后, 以深度图的空间信息聚类分层结果为基准, 提出基于高斯混合模型的光流聚类分割模型.

由于光流是运动物体表面像素点的瞬时速度, 因此, 在同一层局部刚性运动区域物体的光流信息可视作均匀的, 通过从光流中提取运动信息, 可以为同一运动层分割提供可靠的运动信息.此外, 为了降低噪声等因素对光流估计结果的影响, 本文选用Classic+NL^[25]计算RGB图像序列帧间的初始光流.这是因为该方法建立局部加权中值滤波优化方案, 显著提升算法的抗噪性, 并且也是后续很多高精度光流计算模型的基线方法^{[26, 27]}, 甚至还被引入半监督学习光流计算模型^[28].因此基于Classic+NL优越的光流估计鲁棒性能, 可以为本文方法提供稳定的初始光流.

本文引入高斯混合模型, 构建基于高斯混合模型的光流聚类分割模型:

p(w|α, μ, c)= ∑k=1Kα_kN(U|μ_k, c_k).

其中:

∑k=1Kα_k=1, α_k≥ 0,

表示属于第k个高斯的概率; p(· )表示学习到的概率密度; k表示类别; U表示初始光流, U=(u, v)^T, u表示光流水平方向分量, v表示光流垂直方向分量; μ_k表示第k个类别的期望; c_k表示第k个类别的高斯函数协方差矩阵; N(U|μ_k, c_k)表示混合模型中的一个类别.由于高斯混合模型可以看作是由K个单高斯模型组合而成的模型, 因此, 通过习得的概率密度函数, 可以在实现高精度聚类的同时简化信息量.

为了优化基于高斯混合模型的光流聚类分割模型, 本文使用K均值算法为模型提供初始化参数, 则基于高斯混合模型的光流聚类分割模型初始化参数可设置为:

α_k= NskN, μ_k= ∑i=1NskUiNsk, c_k=c(s_k)+βE, (1)

其中, s_k表示第k个聚类, Nsk表示第s_k个聚类中像素点总个数, N表示整幅图像中像素点的总个数, U_i表示第k个聚类中第i个像素点对应的光流值, β表示协方差矩阵的正则化系数, E表示单位矩阵.

在模型初始化后, 通过式(1)可得到模型的后验概率γ(h_ik), 即第k个聚类对图像中第i像素点处光流值U_i的响应度:

γ(h_ik)= αkN(Ui|μk, ck)∑k=1KαkN(Ui|μk, ck), (2)

其中, h_ik为隐变量, 表示第i个光流值属于第k个类别.

利用式(2)得到的响应度不断迭代更新:

$\begin{aligned}& \boldsymbol{\mu}_k^{t+1}=\frac{1}{N_k} \sum_{i=1}^N \gamma\left(h_{i k}\right) \boldsymbol{U}_i, \\ & \boldsymbol{c}_k^{t+1}=\frac{1}{N_k} \sum_{i=1}^N \gamma\left(h_{i k}\right)\left(\boldsymbol{U}_i-\boldsymbol{\mu}_k^{t+1}\right)\left(\boldsymbol{U}_i-\boldsymbol{\mu}_k^{t+1}\right)^{\mathrm{T}}, \\ & \alpha_k^{t+1}=\frac{N_k}{N}, \end{aligned}$

直到达到迭代停止条件

| (lnL(Ui, hik|α, μ, c))t+1- (lnL(Ui, hik|α, μ, c))t≤ ε

时停止, 其中, L(· )表示对数似然值, ε=e^-6表示迭代停止阈值, t表示迭代次数.

本文通过对比光流样本点对各个分模型的响应度大小, 判断样本所属的类别, 确定最终光流聚类分割结果.

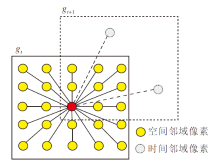
在实际计算中, 本文将包含运动物体的部分划分为前景, 将所有未分配给前景的像素部分归为背景.随着场景运动的变化, 前景与背景的划分并不能始终保持不变.为了在图像序列场景运动过程中动态识别前景区域和背景区域, 避免背景误分为前景的情况, 本文引入层支撑函数g.假设场景包含K个独立运动的运动层, 为了建模不同的前景分割层, 本文使用K-1个连续的层支撑函数g编码不同层像素属于对应前景层的可能性.由于第K层为背景层, 因此不使用层支撑函数.例如, 第t帧第k层(1≤ k≤ K-1)的支撑函数可以表示为g_tk, 编码像素在第t帧属于第k层的可能性.

层支撑函数g的结构如图4所示, 图中g_t表示第t帧前景支撑函数结构, gt+1表示t+1帧的前景层支撑函数, 圆圈表示像素点, g_t中红色像素点表示中心像素点, 在空间上与当前层所有像素关联, 在时间上与2个时间相邻像素关联(图中的灰色像素点), 并且这2个灰色像素点可由光流确定.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 前景层支撑函数的二进制掩码时空结构Fig.4 Space-time structure of binary mask of foreground layer support function

随着时间的变化和运动的变化, 本文通过支撑函数捕获前景层的变化, 并对前景层像素点的可见性进行判断, 即像素点在g_t和 gt+1中均可见时, 属于前景层, 如果不可见, 属于背景层.通过该方法可以在图像序列运动过程中动态区分背景与前景, 从而在一定程度上避免背景被误分为前景的现象.

层支撑函数捕获前景变化的过程可公式化.首先, 利用高斯条件随机场(Markov Random Field, MRF)捕获层支撑函数在空间的一致性:

$\begin{aligned} & E_g\left(g_{t k}\right)=\sum_{\boldsymbol{x}} \sum_{x^{\prime} \in N_{\boldsymbol{x}}}\left(g_{t k}(\boldsymbol{x})-g_{t k}\left(\boldsymbol{x}^{\prime}\right)\right) \omega_{\boldsymbol{x}^{\prime}}^{\boldsymbol{x}}, \end{aligned}$

其中, x=(x, y)^T表示像素点坐标, N_x为x的最近四邻域像素集合, x'为四邻域像素.此外, 在边缘区域使用颜色矢量差异作为权重 ωxx', 保护边缘.权重 ωxx'定义为

$\begin{aligned} & \omega_{\boldsymbol{x}^{\prime}}^x=\max \left\{\exp \left\{-\frac{I_t(\boldsymbol{x})-\left.I_t\left(\boldsymbol{x}^{\prime}\right)\right|^2}{\sigma_I^2}\right\}, \omega_0\right\}, \end{aligned}$

其中, σ _I表示高斯核的标准差, ω₀表示常量颜色空间平衡系数, 作用是避免图像中局部区域出现颜色矢量变化过大的情况.

最后, 使用高斯MRF保持层支撑函数在时间上的一致性:

$\begin{aligned} & E_t\left(g_{t k}, g_{t+1, k}, \boldsymbol{u}_{t k}, \boldsymbol{v}_{t k}\right)=\sum_x\left(g_{t k}(\boldsymbol{x})-g_{t+1, k}(\tilde{\boldsymbol{x}})\right)^2, \end{aligned}$

其中,

x~= (x+utk(x), y+vtk(x))T

表示当前第t帧第k层像素点根据光流运动信息获得的在下一帧对应位置的像素点坐标.

为了降低噪声等异常值因素对深度分层结果的影响, 本文采用文献[15]提出的深度图预处理方法, 掩盖无效的深度测量, 降低噪声影响.然后, 在获取高斯聚类光流分割结果后, 将其与深度分层结果进行对比, 并利用光流信息判定深度分割图中相邻层是否可以合并优化.

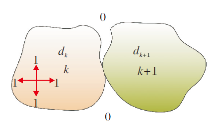
深度分层结果中的相邻层判定方法为:令d_k、d_k+1分别表示深度分层结果中的两个层, k表示d_k层中的标记, k+1表示d_k+1层中的标记.首先, 将第d_k层上下左右移动一个像素点, 再分别和d_k+1层相加.最后, 检测相加后的结果中最大值是否包含2k+1.如果包含, 判定为相邻区域, 进一步利用光流信息判定这两层是否可以合并.如果不包含, 保持原始深度分层结果.该过程如图5所示.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 相邻层判定Fig.5 Adjacent layer judgment

由于在小的局部范围内物体的运动是刚性的, 因此, 可以获取d_k层和d_k+1层的像素点坐标, 然后通过像素点坐标信息映射至对应的光流分层结果中, 从而找到该区域对应的光流分层区域.假设局部范围Ω内的深度分层结果中的相邻层d_k和d_k+1映射到对应光流分割层的区域为f_k和f_k+1, 此时计算光流分割区域f_k、 f_k+1所有像素点光流的平均角误差avg_AE和点误差avg_EE:

$\begin{aligned} & a v g \_A E=\arccos \left(\frac{\overline{\boldsymbol{u}}_{f_k} \overline{\boldsymbol{u}}_{f_{k+1}}+\overline{\boldsymbol{v}}_{f_k} \overline{\boldsymbol{v}}_{f_{k+1}}}{\sqrt{\overline{\boldsymbol{u}}_{f_k}^2+\overline{\boldsymbol{v}}_{f_k}^2} \sqrt{\overline{\boldsymbol{u}}_{f_{k+1}}^2+\overline{\boldsymbol{v}}_{f_{k+1}}^2}}\right), \\ & a v g_{-} E E=\sqrt{\left(\overline{\boldsymbol{u}}_{f_k}-\overline{\boldsymbol{u}}_{f_{k+1}}\right)^2+\left(\overline{\boldsymbol{v}}_{f_k}-\overline{\boldsymbol{v}}_{f_{k+1}}\right)^2}, \\ & \text { s. t. }\left\{f_k, f_{k+1}\right\} \in \Omega, 1 \leqslant k \leqslant K-1 \text {, } \end{aligned}$

其中, u-fk和 u-fk+1表示f_k和f_k+1光流分割区域的水平方向光流平均值, v-fk和 v-fk+1表示垂直方向光流平均值.

判定深度分层结果中相邻层是否可以合并的条件为:当avg_AE< TH_ae或avg_EE< TH_ee时, 合并深度分割层d_k和d_k+1, 否则不合并, 其中, TH_ae和TH_ee为预设置阈值.通过实验分析, 本文设置

TH_ae=0.01, TH_ee=0.004.

值得注意的是, 当包含深度层次不同、但在二维图像投影中连通的两个静止物体时, 因为这两个区域没有发生运动, 光流信息为0, 所以后置光流优化操作并不会优化该区域的层次划分, 深度分层保持不变.这也说明, 本文方法仅适用于运动物体的深度分层优化, 因为运动是光流产生的必要条件.另外, 针对被深度聚类分配至不相邻层的情况, 是否可以合并需要依据物体的运动状态决定.当物体处于静止状态时, 由于没有产生光流优化所需的运动信息, 因此不会被合并.如果物体发生能够被捕捉到的光流运动信息, 可根据光流优化判定方法决定其是否可以合并:1)如果该运动信息满足优化合并判别条件, 合并; 2)如果该运动使物体的状态发生较大变化, 如中断、严重不连续, 导致运动信息差异太大, 则划分至不同层的部分难以被合并.

此外, 为了保证深度分层与光流分层在层次结构的相似性, 在实际计算过程中, 本文遵循文献[29]中的深度聚类合并策略, 对深度聚类分割后的区域先执行一次合并操作, 减少由于距离信息产生的过度分层, 使深度分层结果与光流估计结果更加接近.同时在光流分层时, 为了尽可能实现同层光流的聚类分割, 避免因相同区域光流之间的差异而导致的误分层问题, 本文基于局部刚性假设, 使用局部区域的平均光流代替该区域的全部光流以减缓该问题, 从而保证二者分层结果的相似性.

最后, 本文还采用迭代交替优化方案, 进一步减小噪声等异常值对模型的影响, 即先用Classic+NL计算的光流辅助优化深度分层, 获取初始优化结果, 然后, 利用该深度分层结果进行后续的场景流计算.由于光流本质上是场景流在二维空间的投影, 所以本文利用计算的场景流反作用于优化光流, 并对深度分层结果进行再一次优化.通过多次迭代, 提高深度分层分割精度.

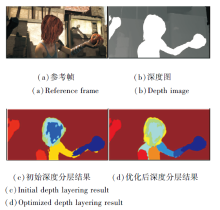
深度运动分层优化前后的结果对比如图6所示.由图可以看出, 初始深度分层结果存在较明显的错误, 如人物身体部分错误地与背景分割为一类, 而优化后的深度分层结果较好地避免该问题.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 深度运动分层优化结果对比Fig.6 Comparison of depth motion layering optimization results

对于给定的连续两帧RGB图像I₁、I₂和对应深度图像D₁、D₂, 本文首先将输入的图像序列依据深度分层分割结果划分为相互独立的运动层, 然后, 将全局运动计算分解成每个独立分割层运动的集合, 进而计算对应的每层运动.

依据运动方向的不同, 将全局运动分解为水平、垂直和深度方向的独立运动, 相应的半参数模型可表示为E_u(u_tk, φ _tk)、E_v(v_tk, φ _tk)、E_w(w_tk, φ _tk), 则

E_u(u_tk, φ _tk)= ∑xγ _b(u_tk(x)- utkR(x))·

∑x'∈Nxγ _u((u_tk(x)- utkR(x))-(u_tk(x')- utkR(x'))),

E_v(v_tk, φ _tk)= ∑xγ _b(v_tk(x)- vtkR(x))·

∑x'∈Nxγ _u((v_tk(x)- vtkR(x))-(v_tk(x')- vtkR(x'))),

E_w(w_tk, φ _tk)= ∑xγ _b(w_tk(x)- wtkR(x))·

∑x'∈Nxγ _u((w_tk(x)- wtkR(x))-(w_tk(x')- wtkR(x'))),

其中, u_tk表示场景流水平分量, v_tk表示场景流垂直分量, w_tk表示场景流深度分量, γ _b、γ _u表示鲁棒惩罚函数, x'=(x', y')^T表示像素点x的局部邻域N_x内的任意像素, φ _tk= (Rtk, Ttk)T表示第t帧中第k层分割层的变换矩阵, R_tk为旋转矩阵, T_tk为平移矩阵.

假设位于相同分割层的对应像素点坐标集合为m_i和n_i, 通过Horn四元数法可以计算每层对应的旋转矩阵R和平移矩阵T, 该过程可公式化为

E(R, T)=min ∑Ω(Rm_i+T-n_i)², (3)

其中, i表示像素点索引, Ω表示图像区域.

由于本文将图像场景分割为相互独立的运动层, 因此, 假设每个分割层中所有像素点均具有相同的运动参数矩阵, 则基于高斯混合模型的RGBD场景流计算模型可表示为

$\begin{aligned} & E(\boldsymbol{u}, \boldsymbol{v}, \boldsymbol{w}, g, \boldsymbol{\varphi})= \\ & \sum_{t=1}^{T-1}\left\{\sum_{k=1}^K\left\{E_{\mathrm{data}}\left(\boldsymbol{u}_{t k}, \boldsymbol{v}_{t k}, g_t\right)+\lambda_d E_{\mathrm{depth}}\left(\boldsymbol{u}_{t k}, \boldsymbol{v}_{t k}, \boldsymbol{w}_{t k}\right)+\right.\right. \\ & \left.\lambda_m\left\{E_u\left(\boldsymbol{u}_{t k}, \boldsymbol{\varphi}_{t k}\right)+E_v\left(\boldsymbol{v}_{t k}, \boldsymbol{\varphi}_{t k}\right)+E_w\left(\boldsymbol{w}_{t k}, \boldsymbol{\varphi}_{t k}\right)\right\}\right\}+ \\ & \left.\sum_{k=1}^{K-1} \lambda_t E_t\left(g_t, g_{t+1}, \boldsymbol{u}_{t k}, \boldsymbol{v}_{t k}\right)\right\}+\sum_{t=1}^T \sum_{k=1}^{K-1} \lambda_g E_g\left(g_{t k}\right), \end{aligned}$

其中, λ _d表示深度图约束项权重, λ _m表示全局运动分解约束项权重, λ _t表示时间约束项权重, λ _g表示空间约束项权重, E_data(u_tk, v_tk, g_t)表示基于高斯混合模型的光流聚类RGBD数据约束项, E_depth(u_tk, v_tk, w_tk)表示基于高斯混合模型的深度图约束项,

$\begin{aligned} & E_{\text {data }}\left(\boldsymbol{u}_{t k}, \boldsymbol{v}_{t k}, g_t\right)=\sum_x s_{t k}(\boldsymbol{x}) \rho_c\left(\tilde{I}_t(\boldsymbol{x})-\tilde{I}_{t+1}(\tilde{\boldsymbol{x}})\right) \text {, } \\ & E_{\mathrm{depth}}\left(\boldsymbol{u}_{t k}, \boldsymbol{v}_{t k}, \boldsymbol{w}_{t k}\right)=\sum_x s_{t k}(\boldsymbol{x}) \rho_d\left(z_{t+1}(\tilde{\boldsymbol{x}})-z_t(\boldsymbol{x})-\boldsymbol{w}_{t k}(\boldsymbol{x})\right), \\ & \end{aligned}$

I~(x)表示像素点x的灰度特征, z(x)表示像素点x的深度值, ρ _c、 ρ _d表示鲁棒参数, s_tk(x)表示根据高斯混合模型光流聚类分割结果和深度运动分层优化结果定义的图像分层函数,

s_tk(x)= gtk(x)∏k'=1k-1(1-gtk'(x)), 1≤k< K∏k'=1k-1(1-gtk'(x)), k=K

g_tk(· )表示第t时刻第k层支撑函数, 是光流聚类结果得到的二进制掩码, g_tk(· )≥ 0表示像素点属于该层, 否则说明像素点属于其它分割层, 即当s_tk(x)=1时, 该像素点是属于第k层的点.当在计算第k层的场景运动时, 通过图像分层函数将属于该分割层的数据项置为1, 而不属于该分割层的数据项置为0, 从而避免非本层像素点对本文方法计算的影响.

针对场景流计算在图像边缘存在模糊的问题, 本文在RGB数据约束项和深度图约束项中引入双边滤波约束, 在场景流优化计算过程中使用双边滤波优化, 进而达到保护图像边缘目的.加入双边滤波约束后的RGB数据约束项和深度图约束项可写为

$\begin{aligned} & E_{\mathrm{data}}\left(\boldsymbol{u}_{t k}, \boldsymbol{v}_{t k}, g_t\right)=\sum_x b f\left(s_{t k}(\boldsymbol{x}) \rho_c\left(\tilde{I}_t(\boldsymbol{x})-\tilde{I}_{t+1}(\tilde{\boldsymbol{x}})\right)\right), \\ & E_{\mathrm{depth}}\left(\boldsymbol{u}_{t k}, \boldsymbol{v}_{t k}, \boldsymbol{w}_{t k}\right)=\sum_x b f\left(s_{t k}(\boldsymbol{x}) \rho_d\left(z_{t+1}(\tilde{\boldsymbol{x}})-z_t(\boldsymbol{x})-w_{t k}(\boldsymbol{x})\right)\right). \end{aligned}$

其中bf(· )表示双边滤波约束.

为了求解分层场景流中第k层的场景流, 本文首先将t时刻参考第1帧图像中第k层的目标像素点记为p=(x, y)^T, 对应深度值记为z.然后, 计算t时刻到t+1时刻连续图像序列间的帧间光流(u, v)^T, 并由该光流信息计算t+1时刻p点在第2帧图像中对应的位置p'=(x', y')^T, 而

x'=x+u, y'=y+v.

同时, 采用双线性插值算法, 可求得p'点对应深度值为z_w.根据相机映射关系, 将像素点p和p'的坐标映射到相机坐标系, 则两点的坐标可表示为

P=(X, Y, z)^T, P'= (X', Y', zw)T,

即

X= z(x-cx)fx, Y= z(y-cy)fy,

X'= zw(x'-cx)fxY'= zw(y'-cy)fy

其中, c_x、c_y表示相机的中心, f_x表示相机水平方向的焦距, f_y表示相机垂直方向的焦距.

假设在前后两帧图像序列中属于第k层的所有像素点的坐标集合记为A_i、B_i, i=1, 2, …, k, 利用式(3)计算每层的旋转矩阵R_tk和平移矩阵T_tk , 则点p对应的新的三维空间位置可表示为

(X', Y', z')=R_tk· X+T_tk.

依据上式, 其对应的2D位置为

$\begin{aligned} & \left\lgroup f_x \frac{X^{\prime}}{z^{\prime}}+c_x, f_y \frac{Y^{\prime}}{z^{\prime}}+c_y\right\rgroup \end{aligned}$,

则像素平面上的场景流为

u(p)=fxX'z'+cx-x, v(p)=fxY'z'+cy-y, w(p)=zw-z.

最后, 为了保护图像边缘结构, 使用双边滤波约束分别对场景流水平方向分量u, 垂直分量v和深度分量w进行优化, 优化方法如下:

$\begin{aligned} & \boldsymbol{u}^{\prime}\left(p_c\right)= \frac{1}{W} \sum_{p \in N_p} G_{\sigma_s}\left(\left\|p-p_c\right\|\right) G_{\sigma_r}\left(\left|\boldsymbol{u}(p)-\boldsymbol{u}\left(p_c\right)\right|\right) \boldsymbol{u}\left(p_c\right), \\ & \boldsymbol{v}^{\prime}\left(p_c\right)= \frac{1}{W} \sum_{p \in N_p} G_{\sigma_s}\left(\left\|p-p_c\right\|\right) G_{\sigma_r}\left(\left|\boldsymbol{v}(p)-\boldsymbol{v}\left(p_c\right)\right|\right) \boldsymbol{v}\left(p_c\right), \\ & \boldsymbol{w}^{\prime}\left(p_c\right)= \frac{1}{W} \sum_{p \in N_p} G_{\sigma_s}\left(\left\|p-p_c\right\|\right) G_{\sigma_r}\left(\left|\boldsymbol{w}(p)-\boldsymbol{w}\left(p_c\right)\right|\right) \boldsymbol{w}\left(p_c\right), \end{aligned}$

其中, p_c表示中心像素点, N_p表示中心像素点的空间邻域, p表示该空间内像素点, u(p_c)、v(p_c)、w(p_c)表示场景流在像素点p_c处水平、垂直和深度方向的值, W表示归一化常数

W= ∑p∈NpGσs(‖ p-p_c‖ ) Gσr(|I(p)-I(p_c)|),

G_σ (· )表示高斯函数, σ表示标准差, Gσs(· )表示空域核, Gσr(· )表示值域核,

$\begin{aligned} & G_{\sigma_s}=\exp \left(\frac{-\left(p-p_c\right)^2}{2 \sigma_s^2}\right), \\ & G_{\sigma_r}=\exp \left(\frac{-\left|\boldsymbol{u}(p)-\boldsymbol{u}\left(p_c\right)\right|^2}{2 \sigma_s^2}\right) . \end{aligned}$

当优化区域在图像平坦区域时, 该区域像素值变化很小, 像素差值接近于0, 此时空间域权重起主要作用, 对图像进行去噪.当优化区域在图像边缘区域时, 该区域像素值变化较大, 像素值差值较大, 此时值域权重起主要作用, 保护图像边缘信息.

以连续多帧图像序列场景流计算效果对比为例, 在引入多通道双边滤波约束前后, 场景流计算效果的差异如图7所示.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 引入多通道双边滤波约束前后场景流计算效果对比Fig.7 Comparison of scene flow calculation effects before and after introducing multi-channel bilateral filtering constraints

由图7可以看出, 未引入多通道双边滤波约束时, 场景计算结果在边缘区域包含较明显的模糊与异常值.加入多通道双边滤波约束后, 场景流计算结果在边缘区域更加清晰, 异常值大幅减少.上述情况说明本文引入多通道双边滤波约束, 可以有效抑制图像边缘的模糊与异常值现象, 对提高场景流计算效果具有显著作用.

本文采用场景流计算研究中普遍采用的光流异常值百分比(Fl-all)^[24]、平均角误差(Average Angu-lar Error, AAE)和均方根误差(Root Mean Squared Error, RMSE)^[23]指标, 从异常值、角度与幅度三方面对场景流计算结果进行量化评价:

$\begin{aligned} & F l \text {-all }=\frac{P}{A L L} \times 100 \%, \\ & A A E=\frac{1}{N} \arccos \left(\frac{1+\boldsymbol{u}_{\mathrm{GT}} \boldsymbol{u}+\boldsymbol{v}_{\mathrm{GT}} \boldsymbol{v}}{\sqrt{\boldsymbol{u}_{\mathrm{GT}}^2+\boldsymbol{v}_{\mathrm{GT}}^2+1} \sqrt{\boldsymbol{u}^2+\boldsymbol{v}^2+1}}\right), \\ & R M S E= \\ & \sqrt{\frac{1}{N} \sum_{(x, y)}\left(\left(\boldsymbol{u}_{\mathrm{GT}}(x, y)-\boldsymbol{u}(x, y)\right)^2+\left(\boldsymbol{v}_{\mathrm{GT}}(x, y)-\boldsymbol{v}(x, y)\right)^2\right)}, \end{aligned}$

其中, P表示光流端点误差大于3个像素的像素点个数, ALL表示整幅图像所有的像素个数, (u, v)^T表示光流计算值, (uGT, vGT)T表示真实光流值.

Fl-all表示光流异常值百分比, 反映计算值偏离真实值超过一定阈值时离群像素点占整幅图像总像素点个数的百分比.AAE为平均角误差, 反映光流计算值与光流真实值之间的角度误差.RMSE为均方根误差, 遍历图像中的所有像素, 将算法获取的三维场景流映射为二维光流, 并与真实光流值进行对比, 反映误差分布和整体准确度水平.

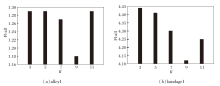
由于本文方法使用K均值进行参数初始化, 因此, K均值中K的设置对本文方法计算效果存在一定影响.本文使用MPI-Sintel数据集的测试图像集上alley1、bandage1图像序列进行参数设置实验, 分析不同K值对本文方法场景流计算的影响, 实验设置K=3, 5, 7, 9, 11.

不同K值对本文方法场景流计算精度的影响如图8所示.由图可以看出, 随着K值的增加, 场景流计算的Fl-all值呈现先降低后增大的趋势, 当K=9时, Fl-all值达到最高.因此, 本文方法设置初始分层数K=9.

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 不同K值对Fl-all的影响Fig.8 Effect of different K on Fl-all

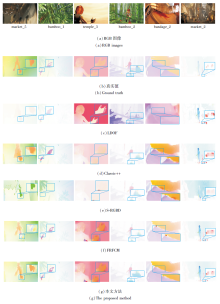
首先采用Middlebury数据集上提供的标准测试图像序列验证本文方法场景流计算的准确性与边缘保护效果.选取S-RGBD^[19]、Classic++^[25]、LDOF(Large Displacement Optical Flow)^[30]、FRFCM(Fast and Robust Fuzzy C-means)^[31]作为对比方法.Classic++采用经典鲁棒参数变分模型, 在优化过程中采用中值滤波去除光流结果中的异常值.LDOF是基于特征匹配与金字塔变形策略结合的计算方法.S-RGBD利用深度图进行深度分割排序, 并结合光流计算每层的运动, 最后使用金字塔分层变形技术优化各层场景流.FRFCM对光流彩色编码结果进行聚类, 并利用深度信息优化聚类结果, 计算场景流.

各方法在Middlebury数据集测试图像序列上的RMSE和AAE统计结果如表1所示.从表中可以看出, 本文方法仅在Laundry、Moebius、Books图像序列上的RMSE和AAE值略低于FRFCM, 而在Art、Reindeer、Dolls图像序列上, 本文方法的RMSE和AAE值最低.相比FRFCM, 本文方法的RMSE值降低74.69%, AAE值降低36.36%.以上说明本文方法针对具有大位移运动、运动遮挡等复杂场景的图像序列场景流计算具有较高的准确性与鲁棒性.

表1

Table 1

表1(Table 1)

表1 各方法在Middlebury数据集图像序列上的场景流计算误差统计 Table 1 Calculation error statistics of scene flow of different methods on images sequence of Middlebury dataset 图像序列 LDOF Classic++ S-RGBD FRFCM 本文方法 RMSE AAE RMSE AAE RMSE AAE RMSE AAE RMSE AAE Laundry 22.91 2.41 46.08 34.29 0.39 0.18 0.26 0.16 0.25 0.16 Art 11.96 1.53 8.39 1.14 1.69 0.77 0.97 0.22 0.20 0.14 Reindeer 62.07 1.62 7.07 0.44 4.24 0.54 3.08 0.43 0.23 0.17 Moebius 12.39 1.09 18.86 5.80 0.17 0.13 0.17 0.13 0.17 0.12 Books 10.82 2.02 23.75 15.10 0.13 0.15 0.13 0.16 0.12 0.14 Dolls 10.67 1.02 18.28 0.55 0.53 0.38 0.40 0.20 0.27 0.12 平均值 37.38 1.62 20.40 9.55 1.19 0.36 0.83 0.22 0.21 0.14

表1 各方法在Middlebury数据集图像序列上的场景流计算误差统计 Table 1 Calculation error statistics of scene flow of different methods on images sequence of Middlebury dataset

各对比方法在Middlebury数据集图像序列上的可视化结果如图9所示, 相应标签局部放大图如图10所示.由图9可见, 在场景流整体计算效果方面, Classic++由于使用基于加权中值滤波的计算策略, 产生过度平滑的现象, 尤其是在Moebius、Books、Dolls等具有大位移运动和遮挡场景图像序列上存在明显错误计算.由于Middlebury图像序列上包含大位移运动产生的遮挡区域, LDOF的局部区域匹配策略无法获得正确的匹配结果, 导致算法计算效果较差.S-RGBD由于使用基于深度图像的分层计算策略, 场景流计算结果产生边缘模糊现象, 尤其在Art、Laundry图像序列上产生强遮挡区域.

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 各方法在Middlebury数据集测试图像上的可视化结果Fig.9 Visualization results of different methods on test images of Middlebury dataset

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 图9中标签区域的局部放大图Fig.10 Partial enlargement of labeled area in Fig.9

由图10可以看出, 在Laundry图像序列上, LDOF和Classic++存在明显的计算错误, 整个区域的场景流信息丢失严重.S-RGBD和FRFCM较准确地计算出标签区域场景流信息, 但是在边缘区域存在较多的异常值.本文方法不仅完整地计算出标签区域的场景流, 而且在边缘区域消除异常值.在Art图像序列上, 本文方法效果优于LDOF、Classic++和S-RGBD.相比FRFCM, 本文方法效果与其相似, 但是在数值精度方面, 本文方法获取更高的计算精度.在Reindeer序列上, 本文方法在边缘区域取得最佳的计算效果, LDOF和Classic++并未计算出边缘信息, S-RGBD和FRFCM在边缘区域存在较严重的扩张错误.实验结果说明本文方法在Middlebury测试集图像序列上的场景流计算效果更接近于真实值, 准确性更高.

为了验证本文方法针对大位移、遮挡等复杂场景的场景流计算效果, 采用MPI-Sintel数据集, 选取Object Scene Flow(本文简记为OSF)^[11]、SceneFlowFields^[13]、S-RGBD^[19]、Flow-ex^[22]、Classic++^[25]、LDOF^[30]、FRFCM^[31]作为对比方法.OSF通过离散标签将超像素平面与对象进行分配, 建立基于MRF的吉布斯能量函数, 有效改善在大位移运动下场景流计算的准确性.SceneFlowFields采用Lucas & Kanade模型计算光流, 通过稀疏匹配的密集插值结合立体图像视差, 得到密集的场景流.Flow-ex为基于光学膨胀的场景流计算模型, 根据光学膨胀获取深度信息, 通过深度信息结合光流重构场景流.

本文先将MPI-Sintel数据集按照运动场景的不同划分为大位移场景和运动遮挡场景两类, 并针对这两类场景图像序列进行测试.各方法针对大位移场景和运动遮挡场景的Fl-all值如表2所示, 表中黑体数字表示最优值.由于文献[22]中并未提供完整的测试结果数据, 因此本文仅列出已有数据进行对比分析.由表可以看出, 在针对大位移情况场景流计算时, 本文方法Fl-all值整体最优, 相比FRFCM, 在数值精度方面具有明显提升.在针对运动遮挡场景光流计算时, 本文方法在平均值上整体最优.在cave_4、ambush_2、market_2场景上, 相比FRFCM, 本文方法精度具有明显提升.虽然在bandage_2、bamboo_2图像序列上精度略低于FRFCM, 但差距很小.实验结果说明本文方法在针对大位移和运动遮挡情况下的场景流计算时, 具有较高的计算精度与鲁棒性.

表2

Table 2

表2(Table 2)

表2 各方法在MPI-Sintel数据集上Fl-all值统计 Table 2 Fl-all value statistics of different methods on MPI-Sentel dataset 场景 图像序列 LDOF Classic++ S-RGBD OSF SceneFlowFields Flow-ex FRFCM 本文方法 大位移 market_5 42.45 38.78 86.76 29.58 40.77 - 40.57 38.02 alley_1 2.75 2.22 9.84 7.33 5.94 - 1.32 1.18 allay_2 2.75 1.99 39.87 1.44 2.85 - 1.23 1.2 bamboo_1 3.58 2.82 1.9 4.04 6.11 - 2 2.01 temple_3 49.9 41.56 62.18 81.39 72.28 48.52 42.79 41.21 平均值 20.29 17.47 40.11 24.76 25.59 17.58 16.72 运动遮挡 cave_4 16.39 19.57 69.76 33.94 15.63 20.76 16 15.26 bandage_2 5.59 4.63 20.9 13.12 10.72 4.67 3.77 3.78 ambush_2 89.02 80 98.46 87.37 90.92 76.19 82.66 78.85 market_2 7.09 6.73 7.93 10.08 7.11 - 5.43 5.23 bamboo_2 5.52 5.25 4.72 4.86 5.84 6.33 3.91 4.01 平均值 24.72 23.24 40.35 29.87 26.04 22.35 21.43

表2 各方法在MPI-Sintel数据集上Fl-all值统计 Table 2 Fl-all value statistics of different methods on MPI-Sentel dataset

各方法针对大位移与运动遮挡场景流计算的可视化结果如图11所示.由图可以看出, 在大位移场景中, 本文方法在market_5、temple_3图像序列的人物脚部、手部区域明显优于对比方法, 相比FRFCM, 本文方法场景流计算更准确, 较准确地计算出market_5图像序列标签脚部区域场景流, 同时, 大幅消除temple_3图像序列标签手部周围区域的异常值.在bamboo_1图像序列上, 本文方法是唯一计算出木棒区域场景流信息的方法.针对运动遮挡场景, 本文方法场景流计算效果仍然优于对比方法, 且与FRFCM差异明显.在bamboo_2、market_2标签区域, 本文方法均较完整地计算出该区域的场景流, 而FRFCM在bamboo_2标签区域丢失大量运动信息, 在market_2标签区域的边缘处存在明显的异常值与粘连, 并未完全分离出相邻的两个运动物体.实验结果进一步说明, 本文方法在针对大位移和运动遮挡场景流计算时具有较好的计算效果.

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 各方法在MPI-Sintel数据集测试图像上的可视化结果Fig.11 Visualization results of different methods on test images of MPI-Sentel dataset

最后, 为了验证本文方法的鲁棒性, 选用SRSF数据集^[23]进行测试. SRSF数据集主要由真实场景组成, 包含非刚性形变、遮挡、大位移等运动场景.由于该数据集并未提供场景流真实值, 因此, 本文采用场景流计算可视化结果进行定性对比分析.各方法在SRSF数据集上的可视化结果如图12所示, 其中, 第1列场景为手部旋转运动, 第2列为非刚性形变运动, 第3列为既包含大位移又包含运动遮挡的复杂场景.由图可以看出, 在第1幅图像上本文方法效果明显优于对比方法, 更加精确地捕捉到手部运动信息.在包含非刚性形变运动的第2列图像序列, 本文方法效果仅低于S-RGBD, 这说明本文方法在针对非刚性形变运动场景流计算时存在一定限制, 但是在边缘处, 本文方法保持较高精度的计算效果.在第3幅图像上, 本文方法效果相对优于Classic++、LDOF和DSRSF, 相比S-RGBD, 尽管在背景区域效果欠佳, 但获得更准确的人物头部运动信息.这说明本文方法在应对包含真实复杂运动情况下的场景流计算仍然具有较高的计算精度与鲁棒性.

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 各方法在SRSF数据集测试图像上的可视化结果Fig.12 Visualization results of different methods on test images of SRSF dataset