路径积分最早可追溯到20世纪中叶的惯导系统.该系统主要依赖陀螺仪和加速度计, 通过积分加速度实现位置估计^[16].这种方法在早期航空和导弹导航中得到广泛应用, 但容易受到振动、温度变化和传感器漂移的影响, 无法长期维持精度.

为了缓解其局限性, 后续研究引入概率滤波方法.EKF（Extended Kalman Filter）^[17]是一种经典的计算框架, 在机器人轨迹跟踪领域得到广泛应用.但是, EKF计算复杂度较高, 在高度非线性或动态环境中容易出现滤波发散.

粒子滤波作为另一种概率方法, 通过蒙特卡罗采样表示状态分布, 进一步提升非线性处理的鲁棒性^[18].然而, 粒子滤波的计算开销更大, 尤其是在高维状态空间中.

随着视觉和激光雷达的兴起, 路径积分技术进一步演化.视觉里程计利用相机捕获的图像序列估计机器人运动, 通过特征匹配和位姿优化实现路径积分^[19].激光SLAM技术结合激光雷达数据, 同时进行定位与地图构建, 提升结构化环境中的导航精度^[20].

作为大鼠执行路径积分的核心神经元, 内嗅网格细胞和海马位置细胞的放电模型受到学者广泛关注.

网格细胞放电模型主要包含OI（Oscillatory Interference）^[21]和CAN（Continuous Attractor Network）^[22].OI认为网格细胞放电是由多个不同频率的振荡器相互干涉形成.该类模型能解释网格细胞的一些特征, 如网格间隔的比例关系、网格方向的偏移等, 但容易受到振荡器的稳定性、干涉的同步性等影响.CAN认为网格细胞的放电是由神经元之间的循环连接和抑制作用形成的.该类模型能解释网格间隔的离散性、网格方向的一致性等特征, 但容易受到波包的形成机制、移动方式等影响.Zhang等^[23]的研究也发现支持CAN的证据.

位置细胞的单峰放电野一直被认为是由多个具有不同空间尺度的网格细胞模块产生的.因此, 多个计算模型展示网格-位置映射机制, 包括固定权重的突触连接^[24]、异突触Hebb学习规则^[25]、竞争性神经网络^[26]及其它不同种类的神经网络等, 均可成功模拟生理学上位置细胞的放电模式.周阳等^[27]还实现智能体在给定空间内的定位, 但模型需要预训练, 无法自发形成映射关系.

然而, 位置细胞同样接受来自非网格细胞结构的信息投射^[28], 如边界细胞和Theta细胞.边界细胞主要为位置细胞提供边界信息, 并不参与路径积分的计算过程.Theta细胞以自运动线索为输入, 产生VCO（Velocity-Controlled Oscillator）信号编码特定的相位关系, 形成具有单峰放电活动的位置细胞, 从而表征空间位置^[29].

因此, 仅以网格细胞为输入的位置细胞模型无法充分表现其空间编码机制, 对位置细胞接收多源输入的特性进行建模越发重要.

空间细胞通过整合自运动信息维持对位置的连续估计.早期研究提出自旋玻璃模型以模拟内嗅皮层中的路径积分机制, 其中CAN可实现网格细胞的周期性放电^[30].Bjerknes等^[31]将此扩展到发育中的位置细胞, 揭示大鼠幼年期路径积分功能的出现, 并在三维环境中验证模型的鲁棒性.2008年, Milford等^[32]提出RatSLAM, 核心是由位姿细胞组成的三维CAN, 不仅具备实现路径积分的能力, 还能表征智能体的方向.2022年, Dumont等^[33]提出基于尖峰神经网络的路径积分模型, 使用SSPs（Spatial Semantic Pointers）桥接神经和符号表示, 能精确跟踪随机路径上的位置, 并在工作记忆模块中实现短期地图存储和检索.2025年, Li等^[34]提出RC-HMM（Road-network-Constraint Hidden Markov Model）, 通过模仿头方向细胞和网格细胞的动态路径积分方法, 实现在稀疏环境中的高效认知地图构建.

此外, 于乃功等^[35]在前期研究工作中也提出基于鼠脑内嗅-海马认知机制的移动机器人空间定位模型, 以网格细胞作为唯一输入, 驱动位置细胞放电, 并通过离线训练得到的权重固定的神经网络实现路径积分.与之相比, 本文改进如下.

1）多源输入的神经机制.本文引入Theta节律调制的VCO信号作为位置细胞的第二独立输入, 与网格细胞信号实时融合, 不仅更符合生理学事实, 也显著增强积分误差的抑制能力.

2）Hebb在线学习规则实现的可塑性机制.本文采用在线竞争性Hebb学习, 使连接权重在探索中自发调整, 无需预训练即可形成稳定单峰位置野, 更接近真实海马突触可塑性.

3）位置解码算法.本文采用质心法直接对放电率分布加权平均, 能更精确、鲁棒地反映兴奋活动包在细胞板上的几何中心.

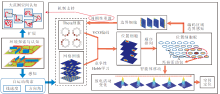
本文提出鼠脑内嗅-海马结构启发的移动机器人仿生路径积分模型（EHPI）, 整体运行机理如图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 EHPI整体运行机理示意图Fig.1 Schematic diagram of overall operating mechanism of EHPI

首先, 机器人通过传感器采集自运动信息, 输入Theta细胞和网格细胞计算模型.位置细胞通过神经网络结构, 同时接受来自Theta细胞和网格细胞的前向投射, 形成对应空间区域的单峰放电野.Theta细胞和位置细胞之间的神经网络采用固定权重的方式, 而网格细胞和位置细胞之间的网络权重通过竞争型Hebb学习机制进行调整.

为了解算机器人在环境中的位置, 首先建立位置细胞群的放电活动与机器人在物理环境中的真实位置之间的转换关系, 并引入边界细胞对空间细胞的放电活动进行周期性重置, 保证机器人在任意大小空间区域内的定位能力.

鉴于位置细胞具有单峰放电特性, 若将一定数量的位置细胞排列成矩形的细胞板, 在细胞板上也将呈现一个单峰的兴奋活动包.若全体位置细胞的放电野中心位置均匀覆盖某个空间区域, 则该区域能被细胞板编码.当大鼠在空间中移动时, 兴奋活动包在细胞板上的位置也随之移动, 从而模拟位置细胞的路径积分过程.

因此, 本文将位置细胞板及其编码空间区域的形状均设定为正方形.每个位置细胞的放电野中心坐标如下：

$ \boldsymbol{r}_{i j}^{\mathrm{pc}}=\left(\frac{L^{\mathrm{pc}}}{2 N_{x}}+(i-1) \frac{L^{\mathrm{pc}}}{N_{x}}, \frac{L^{\mathrm{pc}}}{2 N_{x}}+(j-1) \frac{L^{\mathrm{pc}}}{N_{x}}\right), $

其中, i、 j分别表示位置细胞在细胞板中所处的行列数, L^pc表示细胞板编码正方形空间区域的边长, N_x表示细胞板边长（即位置细胞个数为 Nx2）.

单个位置细胞随时间和空间响应的放电率如下：

F^pc（t）=F^pct（t）F^pcr（r（t））,

其中, F^pct（t）表示随时间变化的载波信号, F^pcr（r（t））表示随空间位置变化的包络信号.

鉴于本文基于空间细胞的放电机理进行定位, 因此仅需考虑位置对空间细胞放电率的影响.位置细胞随空间响应的包络信号为：

F^pcr（r（t））=max（F orgpcr（r（t））-ϑ _thF maxpcr, 0）.

其中：F maxpcr表示位置细胞的放电率峰值, ϑ _th表示放电率阈值, 确保位置细胞板中只有少部分位置细胞处于兴奋状态;

$\begin{array}{l} F_{\text {org }}^{\text {pcr }}(\boldsymbol{r}(t))= \\ \quad w^{\text {vco_pc }} F^{\text {vco_pc }}(\boldsymbol{r}(t))+w^{\text {gc_pc }} F^{\text {gc_pc }}(\boldsymbol{r}(t)), \end{array}$

表示原始包络信号, F^vco_pc（r（t））表示VCO的输入信号, F^gc_pc（r（t））表示网格细胞的输入信号, w^vco_pc、w^gc_pc表示各信号的权重,

w^vco_pc+w^gc_pc=1.

为了避免信号强度差异的问题, F^vco_pc（r（t））和F^gc_pc（r（t））均为归一化操作之后的值.

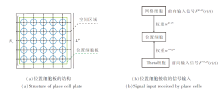
位置细胞板结构如图2（a）所示, 位置细胞接收的信号输入如图2（b）所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 位置细胞板结构及接收的信号输入示意图Fig.2 Structure of place cell plate and received signal input

VCO的相位变化率由自运动线索和Theta节律共同决定.Theta节律表示Theta细胞群的固有振荡活动, 在记忆处理中发挥关键作用.运动速度作为Theta细胞的前向输入信号, 实现特定方向上的路径积分^[29].

第n个VCO的参考相位偏移量：

δ _n（r（t））=δ _n（r（0））+ ∫0td_nv（t）dt=

δ n_（r（0））+dn_（r（t）-r（0））,

其中, r（0）表示大鼠的初始位置, δ _n（r（0））表示第n个VCO的初始参考相位偏移量, v（t）表示时刻t大鼠的运动速度,

d_n=（cos（θ _now-θ _pefer）, sin（θ _now-θ _pefer））,

表示第n个VCO的偏好方向矢量, θ _now表示大鼠当前的方向角, θ _pefer表示第n个VCO的偏好方向.可以看出, 当大鼠在位置r（t）处时, 第n个VCO的参考相位偏移量δ _n严格取决于大鼠当前位置与初始位置的距离 r（t）-r（0）及偏好矢量d_n, 则时刻t的包络信号为：

$F^{\text {vco_pc }}(\boldsymbol{r}(t))=\sum_{n=1}^{N} w_{n} F_{n}^{\text {theta }}(t) .$

其中：w_n表示第n个Theta细胞与位置细胞之间的连接权重;

F ntheta（t）=|exp（iτ δ _n（Δ r^pc））|, （1）

表示时刻t第n个Theta细胞的放电率, τ =γ 2^k-1, γ 表示放电常数, k表示放电野调整系数, 取值为大于0的整数,

Δ r^pc=min（|r（t）-r^pc|, L^pc-|r（t）-r^pc|）,

表示当前位置r（t）与位置细胞放电野中心位置的最小差值, r^pc表示编码位置细胞的放电野中心位置, 通过该方式可避免大鼠靠近编码区域边界时的放电活动缺失.

最后, 利用欧拉公式展开式（1）, 得

F ntheta（t）=|cos（τ δ _n（Δ r^pc））+i sin（τ δ _n（Δ r^pc））|≈

cos（τ δ n（Δ r^pc））.

网格细胞的放电活动同样能被位置细胞利用, 从而更准确表征大鼠位置.然而, 单个网格细胞会导致位置表征的模糊性, 不足以执行路径积分功能, 因此需要不同尺度及方向的网格细胞群编码位置细胞.

本文采用网格神经板, 在固定的网格野上编码不同面积的空间区域, 生成多尺度网格细胞, 具体如图3（a）所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
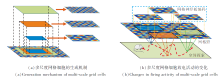	图3 利用网格神经板建模多尺度网格细胞的示意图Fig.3 Schematic diagram of modeling multi-scale grid cells using grid neural plate

当智能体在空间中移动时, 网格神经板类似于一个滑动窗口, 在空间区域内的移动能编码不同区域的网格野, 从而模拟网格细胞放电活动的变化^[36], 具体如图3（b）所示.

首先, 通过振荡干涉获得网格细胞在位置r处的放电率：

$F^{\mathrm{gc}}(\boldsymbol{r})=\frac{2}{3} g_{\max }\left(\frac{1}{3} \sum_{i=1}^{3} \cos \left(\boldsymbol{k}_{i}\left(\boldsymbol{r}-\boldsymbol{r}_{\mathrm{gc}}\right)\right)+\frac{1}{2}\right), $

其中, g_max表示网格细胞放电率的最大值, k_i表示波矢量, r_gc表示网格野位相.网格神经板的形状、尺寸与位置细胞板一致, 编码的正方形区域边长为L^gc.

网格神经板上第i行第j列的神经元在空间中的编码位置为：

rijgc_neuron= rijgc_org+ rijneuron_org,

其中

rijgc_org=( Lgc2Nx+（i-1） LgcNx, Lgc2Nx+（j-1） LgcNx),

表示神经板上第i行第j列的神经元相对于左下角的位置,

rijneuron_org= LgcLpcr-r^gc_max,

表示神经板编码区域左下角在环境中的位置, r^gc_max表示网格细胞产生最大放电率对应的空间位置.

可以看出, r^gc_max、L^gc、L^pc均为定值, rijgc_neuron和F^gc（ rijgc_neuron）均为仅关于r变化的函数.F^gc（ rijgc_neuron）不仅表示网格细胞在位置 rijgc_neuron处的放电率, 也表示当大鼠运动至位置r处时, 网格神经板上第i行第j列神经元的放电率.

为了便于后续计算, 将网格神经板上的神经元放电率也转化为集合的形式, 即

$\begin{array}{l} \text { GC_neuron }= \\ \qquad\left\{F_{1}^{\text {ge_neuron }}(t), F_{2}^{\text {gc_neuron }}(t), \cdots, F_{j}^{\text {gc_neuron }}(t)\right\}, \end{array}$

其中F jgc_neuron（t）表示t时刻在第j层网格神经板上与第i个位置细胞所处行列数相同的网格神经元放电率.

因此, 第i个位置细胞接收网格细胞的反馈输入信号如下所示：

$F_{i}^{\mathrm{gc} \_\mathrm{pc}}(t)=\sum_{j=1}^{N^{\mathrm{gc}}} w_{j}^{\mathrm{gc} \_\mathrm{pc}} F_{j}^{\mathrm{gc} \_ \text {neuron }}(t)-C_{\mathrm{inh}}, $

其中, C_inh表示位置细胞板的全局抑制系数, N^gc表示网格神经板的层数, wjgc_pc表示网格神经板到位置细胞板的神经网络权值, 该值仅与网格神经板的层数有关.

为了保证网格细胞到位置细胞板的反馈信号也是单峰活动, 需要对网络权值 wijgc_pc进行学习.本文使用竞争性Hebb学习规则对 wjgc_pc进行调整, 即

Δ wjgc_pc=ϑ _{gc_pc}F ipcr（r（t））(F jgc_neuron（t）- $\overline{F^{\text {gc_neuron }}}$),

其中, $\overline{F^{\text {gc_neuron }}}$表示集合GC_neuron的平均值, ϑ _{gc_pc}表示学习率.

为了防止学习过程中权值变为负数, 每次权值更新后都将 wjgc_pc约束为大于0的数.

通过竞争性Hebb学习对权值进行调整, 可保证任何时刻都只有一小部分突触权重为正, 而大部分突触权重在学习过程中会收敛为0.因此, 任何时刻都只选择网格细胞群体的一小部分, 确保形成位置细胞群体的单峰活动.

在得到单峰活动的位置细胞板后, 可利用其放电活动完成智能体的空间定位.定义兴奋活动包在细胞板上位置的横纵坐标分别为 Pxt、 Pyt, 在智能体探索过程中使用质心法实时计算其数值, 即

$\left(P_{x}^{t}, P_{y}^{t}\right)=\frac{\sum_{i=1}^{N_{x}} \sum_{j=1}^{N_{x}} F_{i, j}^{\mathrm{pcr}}(\boldsymbol{r}(t)) \cdot(j, i)}{\sum_{i=1}^{N_{x}} \sum_{j=1}^{N_{x}} F_{i, j}^{\mathrm{pcr}}(\boldsymbol{r}(t))}, $

其中F i，jpcr（r（t））表示细胞板上第i行第j列的位置细胞在r（t）处的放电率.为了使模型不仅仅局限于编码区域内的空间认知, 引入对编码区域边界具有特异性放电作用的边界细胞.

设细胞板编码的正方形区域中心位置为r_area, 当智能体到达给定区域空间的任意边界时, 该边界对应的边界细胞会产生放电活动.与此同时, 编码区域中心位置r_area也会被重置.周期性重置过程的表达式如下：

r_area= rarea, BiBthrarea+(rx-Lpc2, Lpc(-1)i-122), Bi≥Bth, i=1, 3rarea+(Lpc(-1)i22, ry-Lpc2), Bi≥Bth, i=2, 4

其中, r_x、r_y分别表示当前时刻智能体在环境中所处位置的横、纵坐标, B_i表示各边界对应的边界细胞放电率, i=1, 2, 3, 4, 分别对应正方形区域的上、左、下、右边界, B_th表示边界细胞的放电阈值.

通过该方式, 每完成一次重置, 位置细胞板就可编码新的空间区域, 实现智能体在任意大小空间区域内的位置认知.在边界细胞的重置机制下, 智能体在空间区域内的位置坐标为：

$ \begin{array}{l} \left(X_{\mathrm{env}}^{t}, Y_{\mathrm{env}}^{t}\right)= \\ \quad\left(\beta\left(P_{x}^{t}-\frac{N_{x}}{2}\right)+Q_{x}, \beta\left(P_{y}^{t}-\frac{N_{x}}{2}\right)+Q_{y}\right) . \end{array} $

其中：β 表示位置细胞板上的坐标向真实位置坐标转换的比例系数, 取值大小等于编码区域的边长L^pc与位置细胞板边长N_x的比值; Q_X、Q_Y分别表示上一次重置时记录的智能体在空间区域内的横纵坐标.

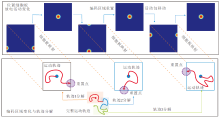
周期性重置下的位置认知运行机理如图4所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 周期性重置下的位置认知机制示意图Fig.4 Schematic diagram of positional cognition mechanism under periodic resetting

为了验证EHPI的性能, 分别设计仿真实验与机器人平台物理实验.仿真实验重点探究EHPI中各类空间细胞的放电模式, 并评估其在智能体沿生理学轨迹运动时的定位性能.物理实验旨在分析EHPI搭载于移动机器人时, 在环境探索过程中的路径积分性能, 并与多种模型进行对比, 评估EHPI路径积分的准确度.

仿真实验均在Dell Optiplex 7080服务器上进行.该服务器配备1块英伟达RTX3070显卡, CPU为Intel I9-10900K, 运行内存32 GB, 操作系统为Windows 10旗舰版.为了提升计算速度, 涉及矩阵的运算均使用GPU进行加速.物理实验分别在室内外环境中进行.在实验过程中, 由于机器人需要接受电脑端发送的运动指令, 故将笔记本电脑置于机器人平台上, 使用无线键盘操控机器人在环境中运动, 通过编码器和IMU传感器采集速度和方向信息.

相关参数设定如下.位置细胞板尺寸为40× 40, 编码正方形空间区域边长L^pc=10 m, 放电率阈值ϑ _th=0.65, 放电常数γ =0.14, 单个位置细胞与12个Theta细胞连接, 神经网络连接权重w_n=1.0.全体网格细胞的网格野相位在编码区域内任意选取, 网格野定向在0~π /2内随机选取, 网格野间距在50~200 cm之间随机选取, 网格细胞放电率的最大值g_max=1.网格细胞个数设为40, 神经板尺寸与位置细胞板一致, 编码的空间区域边长L^gc也与L^pc一致, 学习率ϑ _{gc_pc}=0.02.权重w^vco_pc=0.4, w^gc_pc=0.6, 放电阈值B_th=0.5.

Theta细胞和网格细胞作为海马体和内嗅皮层的重要组成部分, 分别独立与协同影响位置细胞的空间编码能力.下文将验证不同输入源对位置细胞放电活动编码的有效性.首先, 断开网格细胞的输入, 仅考虑Theta细胞作为位置细胞的信息输入源.由于每个位置细胞与12个Theta细胞连接, 因此第i个Theta细胞产生VCO信号的偏好矢量方向为2π （i-1）/12.

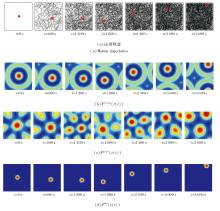
VCO位置细胞放电如图5所示, （a）中放电野调整系数k=3.5.由（a）可见, 每个位置细胞的放电率呈现单峰特性, 随着放电野中心的变化, 放电峰值相应移动, 反映VCO如何通过参考相位偏移量编码位置信息.由（b）可见, 较小的放电野半径对应更尖锐的放电峰, 位置表达更精细, 而较大的放电野半径产生更宽广的放电区域, 增强对噪声的抗扰能力.在后续实验中, 选择k=3.0, 兼顾位置表征的精确性和鲁棒性.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 基于VCO的位置细胞放电效果Fig.5 Place cell firing effect based on VCO

然后, 将Theta细胞的输入断开, 仅考虑网格细胞作为位置细胞的信息输入源.设计10 m× 10 m的二维空间区域, 让智能体在其中随机探索300 s, 记录探索过程中与空间编码相关的各参数变化情况.

基于网格细胞编码的位置细胞放电效果如图6所示.由图可看出, 在智能体探索过程中, 网格神经板能模拟多尺度网格细胞群的周期性放电.同时, 网格神经板到位置细胞板的神经网络权值 wjgc_pc也在竞争性Hebb学习的调整下不断发生变化.这一过程能保证任意时刻只选择一小部分网格神经板以形成单峰输入F^gc_pc（t）, 确保位置表征的局部性和精确性, 避免模糊编码.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 基于网格细胞编码的位置细胞放电效果Fig.6 Effect of place cell firing based on grid cell coding

综上所述, EHPI能有效模拟Theta细胞和网格细胞对位置细胞的投射, 形成可靠的空间编码基础.

下面整合来自Theta细胞与网格细胞的空间信息输入, 模拟位置细胞在海马体中表现的多源信息融合机制.智能体首先在10 m× 10 m的二维空间区域中执行时长为3 600 s的自主随机探索任务, 模拟生物在长时路径积分过程中依赖的持续空间更新过程.此时, 位置细胞板恰好能编码整个空间区域, 故在智能体运动过程中边界细胞不产生放电活动, 空间细胞也不产生放电重置.

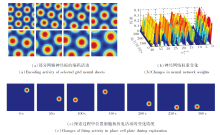
在探索过程中, 同步记录运动轨迹、智能体实时位置、VCO信号F^vco_pc、网格细胞编码信号F^gc_pc、位置细胞板放电活动信号F^pcr的动态演化趋势, 具体如图7所示.在图中, 黑线表示运动轨迹, 红点表示智能体的实时位置.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 智能体在10 m× 10 m空间区域中的探索结果Fig.7 Experimental results of agent exploration in a 10 m× 10 m area

由图7可看出, F^vco_pc、F^gc_pc、F^pcr在智能体整个运动过程中均表现出高度的空间一致性, 能准确追踪智能体的实时位置变化情况, 反映不同空间编码层次之间的协同工作特性.

然后, 将智能体放置在50 m× 50 m的二维空间区域中, 执行时长为500 s的随机探索任务, 验证EHPI在大范围空间中位置编码的有效性.此时, 细胞板无法编码整个空间区域, 需借助放电重置完成空间认知.

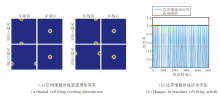
在智能体探索过程中, 穿越不同编码区域边界时空间细胞放电重置效果和边界细胞放电率的变化情况如图8所示.由图可看出, 当智能体穿越当前编码区域的边界时, 边界细胞的放电作用能将编码区域重置到以当前智能体的位置为中心的正方形区域.此时, 位置细胞板上的兴奋活动包也将随编码区域的重置而被重置到位置细胞板的中心位置, 确保在任意大小空间范围内进行路径积分的可行性.

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 智能体在50 m× 50 m空间区域中的探索结果Fig.8 Results of agent exploration within a 50 m× 50 m area

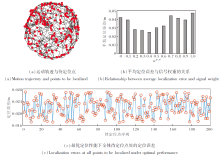
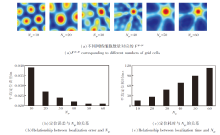
本节对基于空间细胞放电特性的路径积分方法进行2D仿真实验.为了增强实验的说服力, 将Haf- ting等^[37]采集的大鼠在2 m× 2 m真实环境中探索591 s产生的生理学轨迹放大25倍, 作为智能体在空间环境中的运动轨迹.取生理学轨迹上的200个点作为待定位点.在每个待定位点解算智能体的位置, 取解算位置至实际位置的直线距离作为定位误差.智能体沿生理学轨迹运动的定位结果如图9所示, （a）为智能体的运动轨迹与200个待定位点示意图, 黑线表示运动轨迹, 红点表示待定位点.为了探究信号权重w^vco_pc和w^gc_pc（w^vco_pc+w^gc_pc=1）对定位准确度的影响, 分别改变权重大小, 记录每组权重对应200个待定位点的平均定位误差, 如（b）所示.在最优定位性能对应的信号权重下, 全体待定位点处的定位误差结果如（c）所示.

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 智能体沿生理学轨迹运动的定位结果Fig.9 Results of agent localization along physiological trajectories

由图9（b）可看出, 对于定位性能而言, VCO信号F^vco_pc和网格细胞编码信号F^gc_pc呈互补关系.当w^vco_pc或w^gc_pc偏向极端值时, 平均定位误差显著增大.当w^vco_pc过高（VCO信号起主导作用）时, EHPI过度依赖持续的运动节律与矢量线索, 容易受振荡器的稳定性问题和干涉同步性不足的影响, 在复杂动态路径中导致位置估计不精确.当w^gc_pc过高（网格细胞起主导作用）时, EHPI强调周期性的空间锚点, 但缺乏连续动态更新, 容易在非结构化路径中产生定位模糊.多次实验发现, 当w^vco_pc=0.56, w^gc_pc=0.44时, EHPI达到最佳定位性能, 平均定位误差为0.022 m.这一实验结果进一步证实位置细胞多源输入的优势, 即VCO信号提供平滑的运动积分基础, 而网格细胞放电作为离散锚点可降低偏差, 二者在位置细胞层汇聚整合, 形成单一、稳定的位置认知信号.

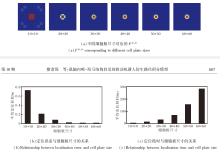
除了信号权重的影响以外, 网格细胞数量和位置细胞板尺寸同样决定模型的定位性能.为了探究其关联, 首先定义网格细胞数量为40, 分别设定位置细胞板的尺寸为10× 10、20× 20、30× 30、40× 40、50× 50、60× 60, 针对不同尺寸的位置细胞板的实验结果如图10所示.

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 不同尺寸位置细胞板的实验结果Fig.10 Experimental results for different place cell plates of varying sizes

由图10可看出, 随着细胞板尺寸增大, 分辨率逐渐提高, 定位误差逐渐降低.原因在于：细胞板的分辨率反映其对位置信息的表征能力, 分辨率越高意味着细胞板越能更精确地表征位置信息.尽管分辨率的提升带来显著优势, 但参与计算的神经元数量也相应增加, 导致计算复杂度增加.这意味着路径积分任务需要更多的计算资源和时间来完成.因此, 权衡定位精度与计算复杂度, 选择40× 40作为后续实验中的细胞板尺寸.

然后, 定义位置细胞板尺寸为40× 40, 分别设定网格细胞数量N_gc=10, 20, 30, 40, 50, 60, 不同网格细胞数量的实验结果如图11所示.

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 不同网格细胞数量的实验结果Fig.11 Experimental results of different numbers of grid cells

由图11可看出, 当网格细胞数量较少时, 编码信号表现出较高的模糊性, 导致位置表征不够精确, 定位误差较大.当网格细胞数量增至40以上时, 意味着竞争性Hebb学习机制能选择更多样化的网格细胞子集, 编码信号F^gc_pc能更好地整合不同方向和尺度的空间信息.这将形成更稳定的单峰输入信号传递至位置细胞板, 从而减少位置模糊性, 降低定位误差.

值得注意的是, 当网格细胞数量大于40后, 再增加也不会显著降低定位误差, 但每次定位所需的计算耗时却与网格细胞数量呈正相关.因此, 权衡定位精度与计算复杂度, 选择40作为后续实验中网格细胞数量.

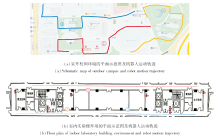
为了进一步突出EHPI的性能优势, 分别设计室内外真实环境下的机器人平台路径积分实验.室外实验在校园中进行, 室内实验在实验楼走廊中进行, 每组实验分别执行3次不同的路径积分任务.室内外环境的平面示意图及机器人执行路径积分任务的运动轨迹如图12所示.

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 机器人路径积分任务示意图Fig.12 Schematic diagram of robot path integration task

将EHPI与EKF（Extended Kalman Filter）^[17]、RatSLAM^[32]、基于SSPs的递归神经网络（后文简记为SSPs）^[33]进行对比, 同时也与直接对角速度和线速度进行积分运算以获取当前位置的模型（后文简记为TPI）进行对比.

室外环境实验直接计算路径积分轨迹与真实轨迹（将智能手机放置在机器人平台上, 通过RTK高精卫星定位获取, 定位误差为± 5 cm）之间的平均绝对误差, 具体如表1所示.各模型输出路径及路径误差变化如图13和图14所示.

表1

Table 1

表1(Table 1)

表1 室外实验中各模型输出轨迹的平均绝对误差 Table 1 Average absolute errors of trajectories generated by different models in outdoor experiments m 任务 TPI EKF RatSLAM SSPs EHPI 路径积分任务① 5.32 4.47 7.45 4.68 2.91 路径积分任务② 4.21 3.45 6.65 4.19 1.61 路径积分任务③ 8.47 2.74 5.83 3.93 2.08 平均性能 5.99 3.55 6.64 4.27 2.20

表1 室外实验中各模型输出轨迹的平均绝对误差 Table 1 Average absolute errors of trajectories generated by different models in outdoor experiments m

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 室外实验中各模型的输出路径Fig.13 Output path of different models in outdoor experiments

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 室外实验中各模型输出路径的误差变化Fig.14 Error changes in output paths of different models in outdoor experiments

由于室内环境无法获取真实轨迹, 故将机器人的运动轨迹设置为直线, 使用卷尺测量机器人路径积分过程始末位置的直线距离, 作为路径长度的真实值.室内实验中各模型输出轨迹的路径长度如图15所示.

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 室内实验中各模型输出轨迹路径长度Fig.15 Path length of trajectories output by different models in indoor experiments

从图13~图15和表1可看出, TPI和RatSLAM的路径误差最大, 室外实验中平均轨迹误差分别为5.99 m和6.64 m, 室内实验中轨迹长度与真实长度的差距也最大.这是因为TPI直接使用原始信号进行计算, RatSLAM同样也是由自运动信息直接驱动三维连续吸引子网络pose cell的放电活动, 无法有效滤除干扰信号.EKF和SSPs的路径误差也相对较高, 室外实验中平均轨迹误差分别为3.55 m和4.27 m.EKF作为一种概率滤波的数学优化框架, 虽然能处理非线性系统的噪声, 但在动态环境中容易出现滤波发散, 无法像生物系统那样通过神经元协作维持稳定的空间表征.SSPs虽基于尖峰神经网络, 桥接神经和符号表示, 但空间语义指针机制更注重抽象的短期记忆存储, 同时也忽略网格细胞的周期性放电模式与边界细胞的特异性响应, 在长期路径积分中难以有效整合连续的自运动线索.

相比之下, EHPI在室外实验中的平均绝对误差仅为2.20 m, 室内实验中的路径积分长度也与真实长度最接近, 展现出显著的低累计误差特性.根本原因在于EHPI从神经生物学层面复现内嗅-海马系统抑制误差的两大核心机制.1）多源异质输入的互补与校正.海马位置细胞同时整合两类在时间特性和误差传播模式上高度互补的驱动信号：Theta细胞调制的VCO信号提供连续高分辨率积分, 网格细胞群提供周期性空间锚点.当VCO信号因噪声或长时间运行发生相位漂移时, 网格细胞在特定相位产生的尖锐放电峰形成强校正信号, 抑制误差增长.2）竞争性Hebb学习实现动态的网格子集选择.不同网格模块之间存在随时间缓慢积累的相位漂移, 但海马位置细胞通过突触可塑性, 仅在每一时刻选择当前相位一致性最高的网格细胞子集构建单峰位置野, 这种“ 赢者通吃” 的动态选择机制相当于生物意义上的“ 误差选择性抑制” , 进一步削弱漂移较大的网格模块影响.