引用本文
孙世光, 兰旭光, 张翰博, 郑南宁. 基于模型的机器人强化学习研究综述. 模式识别与人工智能, 2022,35(1): 1-16
SUN Shiguang, LAN Xuguang, ZHANG Hanbo, ZHENG Nanning. Model-Based Reinforcement Learning in Robotics: A Survey. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(1): 1-16.  
Doi: 10.16451/j.cnki.issn1003-6059.202201001
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于模型的机器人强化学习研究综述
孙世光1, 兰旭光1, 张翰博1, 郑南宁1
1.西安交通大学 人工智能与机器人研究所 西安 710049
通讯作者:

兰旭光,博士,教授,主要研究方向为计算机视觉、机器学习.E-mail:xglan@mail.xjtu.edu.cn.

作者简介:

孙世光,博士研究生,主要研究方向为基于模型的强化学习、机器人控制.E-mail:sunshi.guang@163.com.

张瀚博,博士研究生,主要研究方向为深度强化学习、机器人控制.E-mail:zhanghanbo163@stu.xjtu.edu.cn.

郑南宁,博士,教授,主要研究方向为计算机视觉、模式识别.E-mail:nnzheng@mail.xjtu.edu.cn.

收稿日期: 2022-01-08 接受日期: 2022-01-20
资助项目: 国家重点研发计划项目(No.2021ZD0112700)、国家自然科学基金面上项目(No.62125305,62088102,61973246)、教育部规划项目资助
摘要

基于模型的强化学习通过学习一个环境模型和基于此模型的策略优化或规划,实现机器人更接近于人类的学习和交互方式.文中简述机器人学习问题的定义,介绍机器人学习中基于模型的强化学习方法,包括主流的模型学习及模型利用的方法.主流的模型学习方法具体介绍前向动力学模型、逆向动力学模型和隐式模型.模型利用的方法具体介绍基于模型的规划、基于模型的策略学习和隐式规划,并对其中存在的问题进行探讨.最后,结合现实中机器人学习任务面临的问题,介绍基于模型的强化学习在其中的应用,并展望未来的研究方向.

关键词: 人工智能; 机器人学习; 强化学习; 基于模型的强化学习
中图分类号:TP 181
Model-Based Reinforcement Learning in Robotics: A Survey
SUN Shiguang1, LAN Xuguang1, ZHANG Hanbo1, ZHENG Nanning1
1. Institute of Artificial Intelligence and Robotics, Xi'an Jiaotong University, Xi'an 710049
Corresponding author:
LAN Xuguang, Ph.D., professor. His research interests include computer vision and machine learning.

About Author:
SUN Shiguang, Ph.D. candidate. His research interests include model-based reinforcement learning and robot controlling.
ZHANG Hanbo, Ph.D. candidate. His research interests include deep reinforcement learning and robot controlling.
ZHENG Nanning, Ph.D., professor. His research interests include computer vision and pattern recognition.

Fund:National Key Research and Development Program of China(No.2021ZD0112700), General Program of National Natural Science Foundation of China(No.62125305,62088102,61973246), Program of Ministry of Education of China for Universities
Abstract

The model-based reinforcement learning makes robots closer to human-like learning and interaction by learning an environment model and optimizing policy or planning based on the model. In this paper, the definition of robot learning problems is described, and model-based reinforcement learning methods in robot learning are introduced, including mainstream model learning and model utilization methods. The mainstream model learning methods are given including the forward dynamics model, the inverse dynamics model and the implicit model. The model utilization methods are presented including model-based planning, model-based policy learning and implicit planning. The current problems on model-based reinforcement learning are discussed. Aiming at the problems of the robot learning task in reality, the application of model-based reinforcement learning is illustrated and the future research directions are analyzed.

Key words: Artificial Intelligence; Robot Learning; Reinforcement Learning; Model-Based Reinforcement Learning

本文责任编委 张军平

Recommended by Associate Editor ZHANG Junping

传统的机器人控制大多基于定制化程序解决固定任务, 只适合简单的结构化环境.而对于各种复杂环境下的复杂任务, 机器人本身的最优行为并不唯一, 缺乏固定范式, 因此无法对机器人策略进行预编程[1].近年来, 学习算法的快速发展使解决此类问题成为可能.机器人学习(Robot Learning)是机器学习和机器人技术的交叉领域, 目的是研究让机器人通过与环境自主交互和学习, 获得新技能以适应环境, 使机器人能完成复杂任务.机器人学习涉及计算机视觉、自然语言处理、机器人控制等多个领域的研究.

在强化学习(Reinforcement Learning, RL)[2]中, 机器人可通过与世界环境交互, 从环境中获得反馈并优化自己的行动策略.深度强化学习(Deep RL, DRL)结合深度学习, 使用神经网络表征策略和状态, 对复杂的环境更鲁棒, 更适用于机器人学习中的复杂任务.而基于模型的强化学习(Model-Based RL, MBRL)作为强化学习的一个主要分支, 通常会基于交互信息学习一个环境动力学模型(Dynamics Model), 并基于该模型生成数据优化行动策略, 或利用模型进行规划.无模型的强化学习(Model-Free RL, MFRL)不需要建模, 简单直观, 样本效率较低, 但是渐进性能较高, 适用于游戏领域.而基于模型的强化学习需要学习模型, 学到模型后会有较高的样本效率, 但缺陷是对于有些复杂任务, 模型不容易学到.在机器人控制领域, 模型都有确定的物理规律作为指导, 动作空间相对较小, 模型容易学到, 因此基于模型的强化学习算法更适用.

目前在机器人控制领域, 强化学习算法取得重要进展, OpenAI等[3]通过深度强化学习和虚拟到现实(Sim to Real)的方法, 训练一只可玩魔方的机械手, 灵活性甚至超过人类.相比无模型算法, 基于模型的强化学习算法在机器人上应用更广泛.Levine等[4]基于引导策略搜索(Guided Policy Search), 可让机器人直接从摄像机原始像素中学习灵巧操作, 实现端到端的机器人操作控制.Fazeli等[5]让机器人学习融合视觉和触觉的多模态的推理模型, 结合规划使机器人学会玩叠叠乐(Jenga).Fisac等[6]利用系统动力学模型的近似知识结合贝叶斯机制, 构建机器人控制的通用安全框架, 有效提升机器人操作中的安全性.基于模型的机器人学习算法可从样本中学习一个环境模型, 基于模型学习操作技能, 更适合高维图像输入, 更接近人类的学习方式, 有助于构建人类期望中的机器人.

本文首先从机器人学习问题的建模入手, 介绍马尔科夫决策过程的相关概念, 并将机器人学习问题形式化.详细介绍机器人学习中基于模型的强化学习方法, 包括主流的模型学习及模型利用的方法.主流的模型学习方法具体介绍前向动力学模型、逆向动力学模型和隐式模型.模型利用的方法具体介绍基于模型的规划、基于模型的策略学习和隐式规划, 并对其中存在的问题进行探讨.最后, 结合现实中机器人学习任务面临的问题, 介绍基于模型的强化学习在其中的应用, 并展望基于模型的强化学习未来的研究方向.

1 机器人学习问题的形式化

机器人的长时决策问题[7]通常可表示为一个马尔科夫决策过程(Markov Decision Process, MDP), 用一个五元组表示为(S, A, P, R, γ ).S⊆Rn为状态空间(State Space), 是环境状态(State)构成的集合; A⊆Rn为动作空间(Action Space), 是机器人动作(Action)构成的集合; P(s'|s, a)为状态转移概率(Transition Probability), 描述系统的环境动力学模型, 即机器人在状态s时执行动作a到达下一个状态s'的概率分布; R(s, a, s')为奖励函数(Reward Function), 表示机器人在状态s时执行动作a到达状态s'获得的即时奖励; γ ∈ [0, 1]为折扣因子, 计算累计奖励时降低未来回报对当前的影响.学习的目的是找到一个从状态到动作的映射π, 称为策略(Policy), 使累积折扣奖励 ∑k=0∞γ krk最大化.这样建模可概括机器人学习的任务, 研究人员也可据此研究通用算法.机器人操作的学习问题涉及到学习定义状态空间、学习环境动力学模型、学习运动技能.在机器人强化学习算法中, 状态空间是给定的, 主要学习运动控制策略.环境动力学模型通常是未知的.基于模型的强化学习会通过与环境交互学习环境动力学模型, 以此为基础再进行策略的学习.

将具有相似结构的任务建模为一个MDP的集合(MDPs), 称为一个任务族.使用P(M)表示任务的分布, 每个MDP都是一个特定的任务.任务族中所有任务的动作空间都是相同的, 由机器人决定.但是任务之间的状态空间可能有所不同.第i个任务的状态空间可表示为机器人自身的状态空间和第i个任务环境的状态空间的笛卡尔积:

Si=Sr× Sei,

其中, Sr表示机器人自身的状态空间, Sei表示第i个任务对应环境的状态空间, 可以是原始图像、传感器的数值或预处理的相关任务变量的集合.相应地, 任务族中每个任务的奖励函数也由两部分组成:

Ri=C+Gi,

其中, C表示任务族中公共环境背景的损失函数, Gi表示第i个任务的奖励函数.任务族中的多数任务环境可视为物体集合, 因此也可由描述任务相关物体的变量集合描述.可将环境模型进一步分解为物体状态的集合:

Sei= Swi× Ω1i× …× Ωkii,

其中, Swi为公共的环境背景状态, Ωji为第i个任务中第j个相关物体的状态, ki表示第i个任务环境中包含ki个相关物体.这样建模任务有一个明显的优点, 针对某些物体学到的模型和策略在包含这些物体的新环境中可重复利用[7].

2 基础理论
2.1 强化学习概念

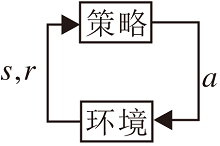
强化学习一般通过马尔科夫决策过程建模, 目标是求解特定任务的最优策略.机器人学习中的长时决策问题也可建模成一个MDP, 因此强化学习适合作为机器人学习的算法.无模型强化学习过程如图 1所示.强化学习的主体称为智能体(Agent).智能体首先对环境进行观测, 得知自身目前所处的状态s, 根据当前状态进行决策, 执行某个动作a, 环境接收到智能体的动作后会转移到一个新的状态s', 同时反馈给智能体一个奖励r=R(s, a, s'), 智能体再次对环境进行观测执行动作, 直到到达终止状态.智能体和环境进行一次完整的交互, 这个过程称为一幕(Episode).记录交互过程中的状态动作, 以时间序列的形式保存, 称为轨迹(Trajectory), 表示为

τ ={s0, a0, ……, st, at, st+1, at+1, …}.

一次交互过程结束时的累积奖励记为

Gt=rt+γ rt+1+γ 2rt+2+…= ∑k=0∞γ krt+k.

图1 无模型强化学习Fig.1 Model-free reinforcement learning

累积奖励中折扣因子γ 的存在降低未来回报对当前的影响.强化学习的最终目标是最大化累积奖励.强化学习过程中智能体通过策略和环境交互, 策略是状态到动作的映射, 可分为随机策略和确定性策略.随机策略会输出一个动作的分布

a=π(·|s),

而确定性策略会输出一个确定性的动作a=π(s).

为了优化策略, 需要评价策略的好坏, 直观方法是对比不同策略在某一特定状态下的累计奖励.在随机策略π下, 计算累积奖励Gt会有多个可能值, 无法进行对比, 但可对Gt求期望, 进行对比.因此定义累积奖励在状态 s 处的期望为状态值函数(Value Function), 简称值函数, 记为

Vπ(s)=E[Gt|st=s].

在某一状态 s 处, 选择不同的动作a会导致不同的累积奖励.定义在状态s处选择动作a的累积奖励的期望为状态-动作值函数(Q Function), 简称Q值函数, 记为

Qπ(s, a)=E[Gt|st=s, at=a].

值函数和Q值函数关系如下[8]:

Vπ(s)=∑a∈Aπ(a|s)Qπ(s, a), Qπ(s, a)=∑s'∈SPss'a[R(s, a, s')+γVπ(s')].

在强化学习问题中, 策略与值函数一一对应, 最优策略对应的值函数称为最优值函数.可证明, 最优策略与最优值函数具有等价性, 该最优值函数满足贝尔曼最优性原理[2]:

V* (s)=max∑s∈SPss'a[R(s, a, s')+γV* (s')], Q* (s, a)=∑s'∈SPss'a[R(s, a, s')+γmaxa'Q* (s', a')].

通常情况下, 可通过迭代解法近似求解最优值函数[2].求出最优值函数后, 可根据最优值函数与最优策略的关系进一步导出最优策略:

π* (s)=arg maxa∈AQ* (s, a).

2.2 基于模型的强化学习

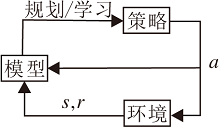
无模型强化学习和基于模型的强化学习的主要区别是机器人决策过程中是否需要环境的动力学模型.无模型的强化学习方法中, 机器人无法知道环境模型, 只能通过不断与环境交互, 收集样本, 优化策略以学习.基于模型的强化学习会学习一个环境模型, 并基于此模型进行策略优化或规划.基于模型的强化学习可定义为:基于一个已知或习得的模型, 学习近似一个全局值函数或策略以求解MDP[9], 过程如图2所示.

图2 基于模型的强化学习Fig.2 Model-based reinforcement learning

根据这个定义中的2个关键点— — 模型学习和策略优化, 可以将基于模型的强化学习划分为3类[9].

1)模型已知, 只需要通过规划学习一个全局值函数或策略.

2)模型未知, 需要学习模型, 基于模型进行规划而不需要学习全局值函数或策略.

3)模型未知, 需要同时学习模型和全局值函数或策略.

在机器人操作领域, 大多时候无法直接得到环境模型, 因此第1类基于模型的强化学习方法应用较少.对于一些棋牌游戏, 规则是人类事先设定, 可直接得到模型, 如用于围棋的AlphaGo Zero[10].第2类方法和第3类方法都需要学习环境模型, 在机器人操作领域应用较多.本文涉及的方法以第2类和第3类为主.

3 学习环境的动力学模型
3.1 模型学习概要

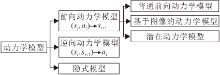
基于模型的强化学习, 学习环境的动力学模型是算法中不可或缺的一步.本文将动力学模型分为3类:1)前向动力学模型, 2)逆向动力学模型, 3)隐式模型.具体如图3所示.

图3 动力学模型分类Fig.3 Dynamics model taxonomy

前向动力学模型根据当前时刻状态和当前动作预测下一时刻的状态, 即(st, at) → st+1, 这是目前应用最广的动力学模型.逆向动力学模型通过当前时刻状态和下一时刻状态推断当前时刻应采用的动作, 即(st, st+1) → at, 这种模型大多应用在基于图像为输入的任务上.隐式模型不关注对下一时刻状态的精确预测.

模型的学习主要有参数化方法和非参数化方法两种.参数化方法是当前通用的模型近似方法, 最基本的形式是表格模型, 但仅能应用于离散状态空间, 在早期的强化学习方法[11, 12]中较常见, 应用受限, 泛化性较差.机器人操作任务的状态空间和动作空间通常都是连续的, 例如, 状态可以是物体的连续位姿、机械臂的关节位置, 动作是机械臂各关节的扭矩.因此环境模型也均为连续模型, 故本文不再讨论表格模型.参数化方法另一形式是函数近似, 通过拟合一个函数以描述系统动力学模型.近似方法有多种, 如线性回归[13, 14]、动态贝叶斯回归(Dynamic Bayesian Networks, DBN)[15]、最近邻[16]、随机森林[17]、支持向量回归[18]和神经网络[19, 20].随着深度学习的发展, 深度神经网络已变为模型学习中最广泛的方法.深度神经网络具有较优的特征提取能力和良好的非线性函数逼近能力, 能扩展到高维图像输入, 契合机器人学习问题.

非参数化的方法主要有高斯过程(Gaussian Processes)[21]和局部加权回归(Locally Weighted Regression)[22].这类模型虽然泛化性能有限, 但样本效率较高.此外, 高斯过程还可用于描述模型中的不确定性.由于非参数化方法的计算复杂度取决于样本数据集的大小, 导致其难以扩展到高维问题.从某种意义上说, 用于存放经验样本的重放缓冲区(Replay Buffer)[23]也算是一种非参数化的模型.van Hasselt等[24]讨论重放缓冲区和参数化模型的区别, 并说明参数化模型在强化学习中的应用时机.

动力学模型还可分为全局模型和局部模型.全局模型近似整个状态空间, 学习到的模型对整个状态空间都是有效的.而局部模型只对动力学模型进行局部近似, 围绕局部模型进行规划.局部模型的优点是在近似环境时可选择简单函数, 如线性函数, 从而可配合某些特定的规划算法.

此外, 对于某些基于强化学习的算法来说, 还需要学习一个奖励函数模型.例如, 利用潜在动力学模型进行策略学习过程依赖于定义在潜在空间上的奖励函数.

3.2 前向动力学模型

3.2.1 普通前向动力学模型

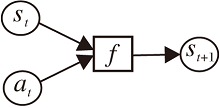
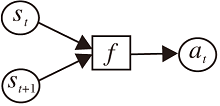
本节描述的普通前向动力学模型是指环境模型中的状态可表示为低维向量的前向动力学模型, 即输入当前状态和动作得到下一时刻的状态, 一般形式是一个确定性函数f(st, at)=st+1或一个随机分布

f(st, at)=P(st+1|st, at),

结构如图4所示.

图4 前向动力学模型结构图Fig.4 Structure of forward dynamics model

模型的学习一般通过监督学习的方式进行.给定当前状态, 机器人执行一个动作和环境交互, 到达下一个状态, 从而得到一组数据样本{st, at, st+1}.收集足够样本后, 可用监督学习的方式学习模型.在基于模型的强化学习算法中, 模型的学习和策略的优化通常迭代进行, 先通过监督学习学到一个模型, 基于此模型进行策略优化, 然后用新策略和环境交互得到数据, 再学一个更精确的模型, 如此迭代进行.

学习到的动力学模型会存在不确定性.不确定性可分为2种:1)固有的随机性, 也称为任意不确定性(Aleatoric Uncertainty), 2)认知不确定性(Episte-mic Uncertainty)[25].固有的随机性是指模型在预测下一步状态时, 会有一个自带的随机性.例如, 掷一个骰子, 落下时朝上的一面是随机的.认知不确定性是指因为数据样本不可能完全覆盖整个状态空间, 所以模型在状态空间的某些区域必定是不准确的.

随机性在机器人操作任务中很常见[22, 26], 通常使用概率模型捕捉噪声并近似估计下一时刻状态的分布.例如, 在均方误差损失上训练一个神经网络f(st, at)时, 实际上该神经网络在学习输出下一时刻状态的均值和方差[27], 通常使用这个均值和方差组成高斯分布, 在分布中采样得到下一时刻的状态.

模型的认知不确定性不同于随机性.随机性源于事物本身, 无法减少.而认知不确定性源于数据不足, 理论上可通过增加样本数据以减小.在解决认知不确定性上较成功的方法是非参数的贝叶斯方法.贝叶斯方法建立概率动力学模型, 捕捉模型预测中的不确定性[21, 28].基于核的高斯过程是目前学习动力学模型通用的贝叶斯方法之一[21, 29].Deisenroth等[30]提出PILCO (Probabilistic Inference for Learning Control), 使用高斯过程对环境动力学进行建模, 得到概率动力学模型, 可表达学习到的动力学模型的不确定性, 并将模型不确定性集成到长期的规划和决策中.高斯过程存在的问题是难以扩展到高维情况.Gal等[31]使用贝叶斯网络代替高斯回归模型, 成功将PILCO扩展到高维系统中.

在神经网络中解决认知不确定性的典型方法如下.Kurutach等[32]提出模型集成(Model-Ensemble)方法, 使用相同真实世界中的样本数据拟合一组动力学模型集合{ fϕ1, fϕ2, …, fϕk}.这些模型的不同仅在于初始权重不同及训练时从真实世界中抽取样本的抽取小批量(Mini-batches)样本的顺序不同.此外在策略优化的过程中随机选择一个模型预测给定当前状态和动作的下一个状态.模型集成的方法减小不确定性, 使学习的过程更稳定, 简单灵活, 在基于模型的强化学习中被广泛应用.模型不确定性目前仍是基于模型的强化学习和深度学习的热点问题之一.

学习到环境模型之后, 可进行规划.规划过程会得到一条决策序列.上述涉及的均是单步预测模型, 在规划过程中反复利用模型进行单步预测, 但是由于存在随机性和不确定性, 学到的模型中会存在误差.而在多次单步预测过程中, 会累积模型误差, 从而导致序列与真实情况相背离.这一问题广泛存在于基于模型的强化学习中[33, 34].

如何获得更好的多步预测, 目前主要有2种方法.1)改进损失函数.Abbeel等[35]提出在模型的训练过程中包括多步的预测损失.通过最大似然法得到模型网络参数:

θ^=arg maxθ∑t=0T-1∑k=1T-tγ k log Pθ(st+k|st).

模型仍然是单步预测, 但是不同于预测下一时刻状态的普通模型, 该模型的损失函数中包括多步之后的预测损失.

2)Asadi等[36]提出学习一个预测n步的动力学模型.模型可表示为

Tn(s, s', π)=Pr(st+n=s'|st=s, π),

即基于当前时刻的状态和未来的动作序列预测当前时刻之后第n步的状态分布.通过实验说明此模型长期预测的累积误差小于单步预测模型.相比预测n步的动力学模型, Mishra等[37]进一步提出预测整个序列的模型.对于多步预测的模型, 如何更好地衡量模型性能也是一个问题.

利用环境动力学模型可大幅提高强化学习的样本效率, 但模型误差会降低基于模型的强化学习的性能, 因此学习模型时如何降低模型的不确定性及控制模型误差是当前的主要挑战.

3.2.2 基于图像的动力学模型

本节讨论基于图像的动力学模型的学习.人类感知环境最基本的方式是视觉.类似于人类, 机器人也可通过摄像头感知环境.此时机器人能接收到的原始状态就是摄像头传递的图像输入, 通常称为观测(Observation).相比普通状态, 图像输入的显著特点就是维度变大.普通低维状态可能从几维到几十维, 而以一幅64× 64的RGB图像作为状态, 维度高达12 288维.高维的难点在于:1)维度增加, 计算量也会大幅增加, 即维度诅咒; 2)高维图像输入中有许多冗余信息, 影响机器人的学习.

高维图像的动力学模型几乎只能靠深度神经网络完成.Levine等[4]实现端到端的机器人操作, 输入图像, 输出动作.经过巧妙推导, 得出不需要学习一个图像转移模型, 而是需要学习一个状态转移模型p(xt+1|xt, ut) 和一个观测分布p(ot|xt)的结论, 并且只在训练中需要观测分布, 在测试时不需要.虽然实现策略以图像输入作为状态产生动作, 但是算法训练过程仍需要知道系统的状态xt, 状态不仅需要包含机器人本身的信息, 还需要知道物体的位置信息等.

Finn等[38]真正提出可应用于机器人的基于图像的环境动力学模型, 利用卷积神经网络(Convolu-tional Neural Network, CNN)和长短时记忆网络(Long Short-Term Memory, LSTM), 可预测从当前帧到下一帧的随机像素流变换(Pixel Flow Transfor-mation), 可在先前帧直接获取图像的背景信息, 合并两者, 能更好地预测未来多步视频序列.该模型真正实现输入机器人状态、动作和图像, 输出下一帧图像, 而不需要标签物体的信息.此后, Finn等[39]进一步将该模型结合规划算法, 真正应用在机器人控制上.

Ebert等[40]基于Finn等的工作进一步改进模型, 提出SNA(Skip Connection Neural Advection Model).SNA可使用时间上的跳跃连接处理遮挡问题, 当一个像素被机器人手臂或其它物体遮挡时, 仍可在序列的后面重新出现.

基于图像的动力学模型还存在部分可观测的(Partial Observability)问题.当观测(Observation)不能提供关于MDP真实状态的所有信息时, MDP会产生部分可观测性.图像观测多数时无法反映真实状态的所有信息, 如环境中有遮挡, 无法知道遮挡后的物体信息.Levine等[4]的方法需要知道真实的状态信息, 因此规避部分可观测性.部分可观测性源于当前观测中信息的缺乏, 但可通过纳入以前的观测信息以部分缓解, 因此Finn和Ebert等提出的基于图像的环境动力学模型都使用循环神经网络(Recurrent Neural Network, RNN)或LSTM, 以此缓解部分可观测带来的问题.

对于部分可观测性还可通过串联n个观测, 作为一个状态来处理.这在以图像为输入的强化学习中较常见, DQN(Deep Q-Network)及其衍生系列算法[41, 42, 43, 44, 45, 46, 47, 48]就使用这种方法.

3.2.3 潜在动力学模型

基于图像的动力学模型的缺点在于需要重构图像, 即使训练好模型, 测试时也需要重构图像, 耗费算力.因此研究者们提出使用表示学习(Representation Learning)结合潜在的动力学模型(Latent Dynamics Model)缓解此问题.表示学习主要用于降维, 本身也是机器学习一个重要研究领域.

一个潜在动力学模型可分为3部分:1)编码器(Encoder)zt=fφ(ot), 将观测结果ot映射到潜在状态(Latent State) zt上; 2)潜在状态转移函数zt+1=fθ(zt, at), 根据当前潜在状态和动作计算得到下一个潜在状态; 3)解码器(Decoder)ot+1=fψ (zt+1), 将潜在状态重新映射回观测.编码器、转移函数和解码器均为深度神经网络, φ、θ、ψ 为对应的网络参数.

潜在动力学模型的重点如下:1)要学到一个足够好的紧凑表示; 2)潜在转移函数能确保进行规划.

当前强化学习中较优的表示学习方法是深度神经网络, 其中生成模型, 如变分自编码器(Variational Auto-Encoder, VAE)[49], 应用尤为广泛.VAE通过最大化条件观测p(ot|zt) 的似然函数进行学习表示, 即需要从潜在状态对观测进行像素级的重构.许多基于模型的强化学习工作[50, 51, 52]在学习表示时都采用VAE.

学到足够好的紧凑表示, 意味着潜在状态能尽可能多地编码观测中的有用信息.通过标准VAE学习表示需要进行像素级重构, 这表明其潜在状态含有与任务无关的信息, 不够紧凑.目前有如下2种思路帮助学习紧凑的表示.1)加入先验知识, 学到一个紧凑表示.Diuk等[53]提出OO-MDPs(Object-Oriented MDPs), 旨在学习到场景中的物体及其交互.这类方法的难点在于如何加入先验知识, 一种方法是通过使用明确的物体识别器.例如, Fragkiadaki等[54]结合物体识别器学习场景中物体运动的规律以泛化到稍有不同的其它环境, Kansky等[55]结合物体识别器, 试图描述物体的局部因果关系并结合到规划中.另一种方法是将先验知识嵌入神经网络结构中.在图神经网络的一些研究中[56, 57], 图的节点对应物体, 边对应物体的关系, 物体间的相互作用通过图神经网络建模.Kipf等[58]提出C-SWMs(Contrastively-Trained Structured World Models), 通过图神经网络对物体的关系进行建模, 并利用对比学习的损失函数进行训练.Watters等[59]采用MONet(Multi-object Network)[60]学习场景的表示, MONet是一个自动回归的VAE, 可在无监督的情况下学习将场景分解为实体, 用于学习更有效的表示.Veerapaneni等[61]提出OP3(Object-Centric Perception, Prediction, and Planning)框架, 试图让机器人理解什么是对象.引入的先验知识为场景中的物体遵循相同的物理规律, 故场景建模可转为对物体和决定物体间交互的局部物理过程的建模, 使用一个以物体为中心的函数(Entity-Centric Function)建模, 再将此函数应用于场景中的每个物体, 简化多物体动态场景.因此OP3可将潜在状态分解为局部物体状态, 每个局部状态均可通过相同的函数进行处理.

2)改进损失函数以学习紧凑表示.典型的做法是结合对比学习(Contrastive Learning)的思想构造对比损失.Ma等[62]结合对比学习, 在标准VAE中使用对比损失替换观测重构项p(ot|zt), 学习一个紧凑表示.Sermanet等[63]构造专家样本时从不同视角记录相同的动作序列, 构造对比损失函数强制同一状态不同视角在潜在空间中相互接近, 以此学习好的表示.Ghosh 等[64]构造基于两个状态之间相互抵达所需动作次数的损失, 使通过较少次数动作就可相互抵达的状态对在表示空间中也较接近.由此学得的紧凑表示更有利于规划.改进损失函数也可和先验知识结合, 即通过改进损失函数体现先验知识.Jonschkowski等[65]将物理学规律作为先验知识, 通过改进损失函数将其引入以学习紧凑表示.Kipf等[58]的方法也可看作引入先验知识和改进损失函数两者的结合.

潜在状态转移函数能确保进行规划意味着要保证转移函数预测的下个潜在状态与编码的当前观测的潜在状态在同个嵌入空间.通常做法是增加一个损失函数, 强制转移函数预测的下个潜在状态接近下一时刻真实观测通过编码器得到的潜在状态[50].此外, 有时还可对潜在状态转移函数进行一些额外限制, 以配合特定的规划算法.例如, 线性二次调节器(Linear Quadratic Regulator, LQR)适用于线性动力学函数, 因此在一些工作[50, 51]中, 研究者将其潜在状态转移函数进行局部线性化, 可应用线性二次调节器进行规划.

潜在动力学模型的研究重点还是在表示学习上, 一个好的表示能提升算法学习与性能.目前许多工作都集中在确保潜在状态尽可能多地蕴含有用信息, 然而一个好的表示也需要尽可能剔除无关信息.如何引入先验知识, 使表示中更多地蕴含有用信息同时剔除无关信息是一个值得研究的问题.

3.3 逆向动力学模型

与前向的潜在动力学模型类似, 逆向动力学模型在强化学习中通常也是和表示学习结合, 即通过编码器将观测ot映射到潜在状态st上, 再通过前后两个时刻的潜在状态预测当前时刻应采取的动作:(st, st+1) → at, 结构如图5所示.逆向动力学模型的引出是因为在状态表征复杂、前向动力学模型学习困难的任务中, 逆向动力学结合某些先验知识效果更优, 同时输出动作可作为监督信息.

图5 逆向动力学模型结构图Fig.5 Structure of inverse dynamics model

Pathak等[66]提出 ICM(Intrinsic Curiosity Mo-dule), 集成逆向模型和前向模型.作者认为使用逆向模型可学习到有用的信息, 忽视无关信息, 由此学到一个好的表示.Agrawal等[67]联合训练前向模型和逆向模型, 在联合训练中, 逆向模型将观测编码为潜在状态, 可为前向模型预测的潜在状态提供监督, 实践中联合损失由逆向模型损失与前向模型损失之和构成.

Shelhamer等[68]将逆向动力学作为辅助的损失函数.初衷是为了增加奖励, 对于强化学习任务, 奖励稀疏意味着缺乏监督, 逆向模型可从相邻状态预测动作.作者指出此动作和与环境交互的动作的误差可起到自监督的作用.Zhang等[69]将表示学习、奖励函数、前向动力学模型和逆向动力学模型进行解耦, 并指出逆向模型在稳定学习方面具有重要作用.

其它一些工作[70, 71, 72]试图利用逆向动力学学习环境中可控制的部分.逆向动力学模型在应用中通常是针对状态表征复杂、前向动力学模型学习困难的特殊任务, 和表示学习结合后形成逆向的潜在动力学模型.主要挑战是如何将逆向和先验知识有机结合, 学到更好的表示.

3.4 隐式模型

一般的前向动力学模型通过当前状态和动作预测环境的下一时刻状态, 这是典型的显式模型.强化学习的最终目的是找到针对特定任务的最优策略.因此真正值得关心的并非状态, 而是最优价值或最优策略.隐式模型通过学习其它函数, 可达到与显式模型相同的效果.相比显式模型, 隐式模型不关注下一时刻状态的精确预测.

Grimm等[73, 74]提出价值等价模型(Value Equi-valent Models), 指出如果一个模型能预测价值, 则状态信息就不再重要, 并说明在相同的贝尔曼算子下, 两个模型对一组函数和一组策略能产生相同的更新, 则这两个模型是价值等价的.Farquhar等[75]进一步提出自洽的价值等价模型.应用价值等价模型的典型例子是MuZero[76].MuZero训练模型时从重放缓存区(Replay Buffer)中选择一条轨迹, 输入第一个状态和整个动作序列, 将模型展开K步, 其中展开的每步动作都是动作序列中的真实动作, 预测奖励值、价值和策略.联合损失函数表示如下:

lt(θ)= ∑k=0Klr(ut+k, rtk)+lv(zt+k, vtk)+lp(πt+k, Ptk)+c‖θ‖2

其中, ut+k、zt+k、πt+k分别表示真实的奖励、价值、策略, rtk、 vtk、 Ptk分别表示预测的奖励、价值、策略.

价值等价模型更早要追溯到Silver等[77]工作.他们的工作与MuZero不同之处在于只接收一个状态作为输入而不需要动作序列, 展开模型只预测该状态的价值.价值预测网络(Value Prediction Network, VPN)[78]与MuZero类似, 但预测奖励、价值和折扣因子.价值等价模型经常也和表示学习结合, 从某种意义上说, 可作为一种先验知识以辅助学习紧凑表示.

隐式模型也存在着一些问题.以价值等价模型为例, 学到的预测都集中在价值和奖励信息上.而这些信息来源于奖励这一简单的标量信息, 因此可能会遗漏环境的一些相关信息.此外, 目前的隐式模型针对的环境动作空间较简单, 大都为离散动作空间, 因此在机器人领域应用较少.

4 模型利用

学习到环境模型之后, 下一步就是如何利用学到的模型.通常在基于模型的强化学习中, 模型主要有3种用途:1)基于模型的规划, 对应2.2节中的第2类方法; 2)基于模型的策略学习, 对应2.2节中的第3类方法; 3)隐式规划, 这是一类特殊的基于模型的强化学习方法, 兼有前两类的一些特点.

4.1 基于模型的规划

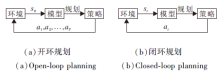
学习到环境的动力学模型后, 可直接利用模型进行规划.强化学习可转化成一个最优控制问题, 通过规划算法得到最优策略, 也可利用规划算法产生较好的样本辅助学习.规划算法种类繁多, 应用广泛, 按照交互方式主要可分为2类:开环规划与闭环规划.开环规划中环境给出初始状态s0, 机器人根据动力学模型规划一条完整的动作序列, 如图6(a)所示.闭环规划中环境给出一个状态, 机器人根据动力学模型进行规划, 执行规划动作, 模型接收到机器人的动作后再给出下一个状态, 往复循环, 如图6(b)所示.

图6 规划过程Fig.6 Planning process

开环规划在强化学习中应用最多的是交叉熵方法(Cross Entropy Method, CEM).CEM的思想是假设动作序列服从某个先验分布, 采样动作得到轨迹, 挑选好的轨迹对先验分布进行后验更新, 具体如下.假设动作服从多元高斯分布A~N(μ, Σ), 第一步, 采样M条动作序列Ai= a1i, a2i, … aTi.第二步, 评估这M条动作序列J(A1), J(A2), …, J(AM), 并按奖励最大或损失最小进行排序.第三步, 挑选出前K条较好的动作序列, 计算均值和方差, 并以此更新高斯分布的参数, 迭代该过程.CEM的缺陷是当动作维度变高时, 规划效果会变差, 适合动作维度较低的简单模型.

由于随机性和不确定性, 模型会存在误差, 如果仅在得知初始状态后进行规划, 可能造成很大的累积误差.这是开环规划本身存在的问题.为了解决这个问题, 引出模型预测控制(Model Predictive Control, MPC).MPC并非一个固定算法, 而是一个控制框架, 可对其进行很多扩展.MPC的思想如下.在每次迭代中, 第一步, 在执行某个动作后, 根据环境动力学模型预测下一个状态.第二步, 求解一个开环优化问题, 这一步可应用某些具体的开环规划算法, 如CEM.第三步, 执行第二步求解的第1个动作, 如此反复进行.可看到, MPC是闭环控制框架, 但在每次迭代中都会优化一个开环控制问题.MPC在基于模型的强化学习中应用广泛, 机器人操作[39, 79]、自动驾驶[80]、无人机[81]等均有应用.CEM经常作为MPC第二步的开环规划算法, 典型算法有Visual MPC[39]、PlaNet(Deep Planning Network)[82].MPC计算量较大, 收敛较慢, 适合简单模型.

闭环规划在强化学习中应用最广泛的是蒙特卡罗树搜索(Monte Carlo Tree Search, MCTS)和线性二次调节器(Linear Quadratic Regulator, LQR).MCTS适用于离散动作空间, 核心搜索过程可分为四步.第一步, 选择.从已知的树节点中根据UCT(Upper Confidence Bounds for Trees)值选择最值得探索的节点.第二步, 扩展.从这个节点选择一个没被执行过的行动, 执行这个行动得到下一个状态, 然后根据这个状态创建节点.第三步, 根据扩展出的子节点, 利用学到的模型进行模拟, 直至结束产生结果.第四步, 回传信息.模拟结束后, 将结果回传给前面所有的父节点, 更新它们的估计值.UCT值的计算公式为

UCTScore(st)= Q(st)N(st)+2C 2lnN(st-1)N(st),

其中, Q(st)表示某个状态的价值, N(st)表示对某个状态的探索次数, st-1表示st的上一个状态, 即父节点.上式平衡探索和利用, 等号后的第1项可看作当前状态的平均价值, 第2项衡量探索次数.参数C调整探索和利用之间的权重关系.可看到, 一个节点要被选中, 必须是价值较大或探索次数较少.MCTS适用于离散动作空间, 在自动驾驶和机器人上均有应用[83, 84].

LQR适用于连续动作空间, 源于控制论, 但在控制领域的符号表示和强化学习有所不同.观测状态st→ xt, 动作at→ ut, 奖励函数变为损失函数r(s, a)→ c(x, u), 最大化问题转为最小化问题.

假设奖励函数r(st, at)为一个二次函数, 而状态转移函数f(st, at)为一个线形函数, 其优化问题形式为

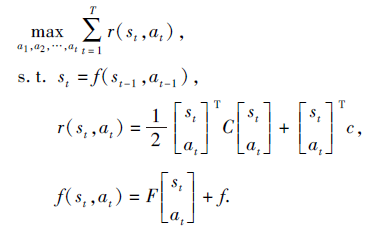
LQR包含反向计算和前向计算, 具体过程可参考最优控制.标准LQR中模型是线性确定的.针对随机模型, 可将高斯分布应用到状态转移函数中, 从而引入随机性.LQR扩展的迭代线性二次调节器(Iterative LQR, iLQR)可应用到非线性模型中.iLQR中的动力学模型近似是一阶近似, 将其扩展到二阶, 就是微分动态规划(Differential Dynamic Programming, DDP).LQR及其扩展方法在基于模型的强化学习中应用广泛.LQR适用于误差较小的模型, 基于引导策略搜索(Guided Policy Search)的一类算法[4, 85, 86]是应用LQR系列规划方法的典型代表.

MPC、CEM存在的问题是计算量较大, 收敛较慢.应用MPC、CEM, 每输入一个状态, 需再次规划才能获取输出动作, 而一个训练好的策略直接将状态映射为动作, 实际应用中训练好的策略比规划算法更快.LQR本身有敏感性的问题, 初始动作中一点微小的改变会导致下游状态变化很大, 模型存在误差时, 这一点尤为严重.因而引导策略搜索一类算法[4, 85, 86]中利用iLQR/DDP产生好的样本以引导策略学习, 最终仍会得到一个策略.

4.2 基于模型的策略学习

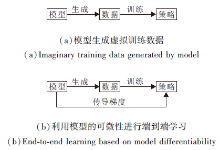
模型的另一种用法就是和无模型的强化学习算法结合, 利用模型辅助无模型强化学习训练策略.可细分为2种:1)通过模型的预测能力生成虚拟训练数据, 如图7(a)所示; 2)利用模型的可微性实现模型学习梯度的端到端反向传播, 如图7(b)所示.

图7 基于模型的策略学习Fig.7 Model-based policy learning

4.2.1 基于模型的虚拟数据生成

这类算法主要是将模型虚拟展开, 生成数据, 混合真实数据和虚拟数据以训练算法, 这也是MBRL样本效率较高的原因.该类算法典型代表是文献[11].由于随机性和不确定性, 模型会存在误差.此外, 用于近似模型的函数也可能存在近似误差, 同时模型误差还会累积传播形成复合误差.如何减小模型误差的影响是一个问题.

Kurutach等[32]通过模型集成表达环境的不确定性, 同时指出建模时数据较少的区域模型误差会较大, 而在这些区域探索会增加模型误差的影响.因此作者在TRPO(Trust Region Policy Optimization)上增加一个迭代阈值, 限制策略朝着环境不熟悉的地方迭代, 以此减小模型误差的影响.

Kalweit等[87]认为误差较大的模型提供的数据质量较低, 会影响算法的最终效果.因此作者把DDPG(Deep Deterministic Policy Gradient)的重放缓存区一分为二, 传统的重放缓存区存储真实环境数据, 想象的重放缓存区存储虚拟环境的数据.通过计算Q值的不确定性, 得到一个动态概率P, 以此决定从哪个重放缓存区中获取数据.这样增加对真实数据的利用, 减少对模型生成数据的利用, 限制模型误差的影响.

Gu等[88]针对环境模型预估不准的问题, 采用基于时间序列的线性模型建模环境, 但为了达到最佳效果, 在训练中会启发式地停用模型.Feinberg等[89]阐明上述方法可能是无效的, 因此提出MVE(Model-Based Value Expansion), 将模型的展开保持在一个固定深度, 控制模型的不确定性, 目标Q值是先通过环境模型模拟H步之后, 再进行Q值估计.于是Q值的估计融合基于环境动力学模型的短期预估及基于目标Q值网络的长期预估, 步数H限制复合误差的累积, 提高Q值的准确性.

Buckman等[90]改进MVE, 提出STEVE(Stocha-stic Ensemble Value Expansion).文章指出MVE要想获得好的效果, 需要依赖调整展开(Rollout)的步数H, 但在复杂环境中H过大会引入较大误差, 而简单环境步数H过小又会减小Q值的估计精度.作者在不同环境中展开特定步数, 计算每步的不确定性, 动态调整及整合不同步数之间Q值的权重, 并且确保仅在不引入重大误差时才使用模型, 以此限制模型误差的影响.

对于模型误差的影响, 有些学者试图从理论上分析.Luo等[91]从理论上说明模型误差的表示, 并量化模型不确定性的指标, 提出SLBO(Stochastic Lower Bound Optimization), 保证算法能单调提升.Janner等[92]针对环境模型和采样可能导致的总偏差C, 提出每次更新后, 策略的累积回报在模型上的改善若大于C, 就能保证在真实环境中提高策略性能.文章提出分支展开(Branched Rollout), 在轨迹中间采样一个状态后, 该状态作为分支点, 展开模型, 训练策略.但由于误差的存在, 只能在模型上展开k步, 文章对k值进行理论分析, 但是策略单调改善的理论分析不够严谨.

Lai等[93]提出BMPO(Bidirectional Model-Based Policy Optimization), 建议另外构造一个后向动力学模型, 同时使用前向模型和后向模型进行展开.由于使用双模型展开, 当展开轨迹的总步数相等时, 前向模型和后向模型各自展开的步数均小于仅使用前向模型展开的步数, 因此复合误差累积显著小于完全使用单向模型的情形.作者通过理论分析和实验验证说明BMPO比MBPO(Model-Based Policy Opti-mization)复合误差更小, 训练效果更优.

4.2.2 基于模型可微性的端到端学习

除了利用模型虚拟展开生成数据外, 如果模型是神经网络或其它可微函数, 还可同时利用模型可微的特点直接辅助策略的学习, 这种方法更进一步利用模型.

Heess等[94]提出SVG(Stochastic Value Gradi-ents), 利用模型的可微性计算值函数的梯度.该文思想较简单, 利用链式法则和模型的可微性直接对值函数求导, 利用梯度上升法优化值函数, 学习策略.对于随机性的环境和策略, 可通过重参数化技巧引入噪声.SVG利用真实样本拟合模型, 利用模型的可微性优化值函数, 在优化过程中只利用真实样本, 并未利用模型产生虚拟数据.这样做的好处是可缓解模型不准确造成的影响, 但同时由于不利用模型产生虚拟数据, 样本效率并未得到较高提升.

Clavera等[95]在SVG的基础上更进一步, 采用执行者-评论家(Actor-Critic)框架, 提出MAAC(Mo-del-Augmented Actor-Critic).除了利用模型的梯度外, 采用H步自举(Bootstrapping)的Q值函数作为强化学习的目标函数:

Jπ(θ)=E[ ∑t=0H-1γ tr(st)+γ H Q︿(sH, aH)].

同时重放缓存区中的数据既有和真实环境交互的数据也有模型虚拟展开的数据.超参数H可使目标函数在模型的准确性和Q值函数的准确性之间权衡.Hafner等[96]提出Dreamer, 值函数估计采用另一种平衡方差和偏差的方式, 但Dreamer是图像输入, 学习潜在模型, 利用潜在模型的H步展开和可微性.

利用模型的可微性延时反向传播计算梯度可能会遇到深度学习中存在的一类问题— — 梯度消失和梯度爆炸.MAAC中采用终端Q函数(Terminal Q-Function)[32]缓解此问题, SVG和Dreamer并未讨论这个问题, 在实现时使用梯度裁剪的技巧.此外, 利用模型可微性还存在容易陷入局部最优的问题.

4.3 隐式规划

隐式规划是一种特殊的基于模型的强化学习方法, 规划过程可嵌入到计算图中, 如图8所示.典型例子是值迭代网络(Value Iteration Network, VIN)[97].VIN设计值迭代模块, 并嵌入CNN中.类似的工作还有UPN(Universal Planning Networks)[98]和QMDP-Net[99].UPN在一个目标导向的策略中嵌入可微分的规划模块.QMDP-Net在一个RNN中嵌入QMDP(Q Values of the Underlying MDP)和贝叶斯滤波器, 求解POMPD(Partially Observable MDP).

图8 隐式规划过程Fig.8 Process of implicit planning

还有一类隐式规划是去学习规划.在一系列任务中优化规划器, 得到更好的规划算法.典型例子是MCTSNets(Monte-Carlo Tree Search Networks)[100].MCTSNets优化MCTS过程中的各个步骤, 如选择、回传和最终的动作输出.另一个例子是I2As(Imagi-nation-Augmented Agents)[101], 设计想象核, 先学习动力学模型, 使用此模型想象未来轨迹.想象的信息会被编码并用于辅助策略的学习.所有模块都整合在一个计算图中.类似的工作还有IBP(Imagination-Based Planner)[102].

隐式规划的缺陷是规划过程中可能会利用任务中的无关特征, 同时计算图通常较大, 计算要求较高, 优化容易不稳定.这些缺点导致隐式规划目前在机器人领域应用较少.

5 在机器人领域的应用与挑战
5.1 在机器人领域的应用

现实中的机器人学习任务面临的问题主要有如下3处.1)高维视觉输入.类似人通过眼睛观察世界, 视觉也是机器人感知环境的重要方式, 研究者们希望机器人能以图像为输入完成操作任务, 不以视觉为输入的机器人犹如盲人摸象, 缺乏实际意义.2)样本效率问题.机器人学习的一个问题是样本效率低下, 无模型的强化学习算法需要和环境交互, 通过试错学习, 这需要大量样本, 对于机器人操作任务, 采样通常麻烦且耗时.3)安全问题.机器人在学习时需要探索, 真实环境中, 无效探索增加机器人的磨损, 因此需要好的探索方法.为了安全起见, 可以在虚拟环境中进行训练, 再迁移到现实世界中, 在虚拟环境中训练策略往往比直接在现实世界中进行更安全.本节从图像输入、样本效率、探索和迁移介绍基于模型的强化学习在机器人上的应用.

高维视觉输入的难点主要有:1)数据维度较高, 计算耗费较大; 2)视觉输入往往是真实环境动力学模型的非线性函数, 导致图像动力学模型的学习及基于此模型的规划非常困难.基于模型的强化学习适合高维视觉输入的任务.Levine等[4]推导不需要学习图像动力学模型, 而是需要学习一个状态转移模型p(xt+1|xt, ut) 和一个观测分布p(ot|xt)的结论, 并且仅在训练策略时需要观测分布, 测试时不再需要, 实现端到端的机器人操作, 输入图像, 机器人会输出动作, 实现操作任务.Finn等[38]通过CNN和LSTM学习前后两帧像素流的变换, 结合先前帧中的背景信息, 真正学到基于图像的环境动力学模型, 可通过机器人当前状态、当前帧和动作预测下一帧, 并结合规划算法, 应用在真实机器人操作上.潜在动力学模型结合表示学习将高维图像观测嵌入低维潜在空间中, 在此低维潜在空间中学习动力学模型及基于模型进行规划都相对容易.许多工作[51, 103]结合潜在动力学模型, 都实现高维图像输入的真实机器人操作任务.

基于模型的强化学习优势是样本效率较高, 因为模型可提供虚拟样本, 因此在机器人控制中, 利用机器人与环境交互得到的真实样本学到一个模型, 利用模型产生大量的虚拟样本以学习策略, 大幅提升样本效率.但是模型误差的存在会降低算法性能, 因此需要更多的真实样本以学习更精确的模型, 提升算法性能, 这相当于降低样本效率.PILCO[30]使用高斯过程表征模型的不确定性, 并将不确定性集成到长期决策中, 将模型误差纳入算法的考虑范围中.因此PILCO可提供高质量的虚拟样本, 实验中只需要七八个迭代周期就解决真实小车倒立摆的控制问题, 只需约4 min就可学习一个复杂物块堆叠任务, 同时使用知识迁移时, 时间可进一步减少到90 s.E2C(Embed to Control)[50]学习一个局部线性的潜在动力学模型, 可结合iLQR进行规划, 在倒立摆的实验中, 平均15次实验就可达到90%的成功率.SOLAR(Stochastic Optimal Control with Latent Re-presentations)[51]利用概率图模型结构学习更精确的潜在动力学模型, 只需要训练2 h就可完成真实环境中以图像为输入的Baxter机器人操作任务.

为了安全起见, 在机器人学习中, 必须限制机器人在真实环境中的探索.当学到环境动力学模型后, 可利用模型辅助探索.Lowrey等[104]学习多个值函数组成内在奖励, 在规划时用于指导探索, 在MuJoCo(Multi-joint Dynamics with Contact)[105]任务和虚拟的机械臂操控魔方上都有不错效果.Sekar等[106]在规划轨迹中计算内在奖励, 使用基于模型的方法最大化规划轨迹中的内在奖励, 预测对未来轨迹的好奇心以增加探索.Nair等[103]学习一个状态的密度模型, 并从中选择目标, 训练机器人完成这个想象中的目标, 在测试时机器人就有可能泛化完成新的目标.这一思想类似Hindsight Experience Replay[107].

在虚拟环境中训练机器人再迁移到现实世界, 可相对保证机器人的安全, 是促进机器人学习相关算法落地应用的重要手段.虚拟到现实(Sim to Real)的迁移关键点为虚拟环境和虚拟到现实的差距(Simulation-to-Reality Gap).目前机器人学习领域常用的虚拟环境主要有MuJoCo[105], Pybullet和Gaze-bo[108].MuJoCo被广泛用于作为强化学习算法性能的测试环境.MuJoCo和Pybullet与深度学习和强化学习的相关库结合较好, 能提供快速训练.Gazebo被集成到机器人操作系统(Robot Operating System, ROS)中, 更适合较复杂的场景.

而针对虚拟到现实的差距目前主要有两类方法— — 域随机化(Domain Randomization)和域适应(Domain Adaption).域随机化的思想为, 不去过多关注虚拟环境和现实的差距, 而是尽可能随机化生成虚拟环境, 尽量覆盖现实环境.域随机化的具体做法有2类.1)视觉随机化, 随机生成的域数据涉及工作台上物体的形状、数目、颜色、纹理、位置、工作台的纹理、摄像机的位置角度、背景的噪声等, 这些不会改变环境动力学模型, 这方面的机器人学习研究主要有Tobin等[109]的工作.2)域随机化是动力学随机化, 虚拟环境中随机生成的数据涉及摩擦系数、关节质量、关节阻尼系数、动作时间步长等, 这些数据的改变会影响环境动力学模型, 这方面的研究有Peng等[110]和Andrychowicz等[111]的工作.视觉随机化和动力学随机化也可结合起来, 如OpenAI灵巧手操控魔方的工作[3].域适应的重点是可获取少量真实环境的一些知识, 结合到虚拟环境的训练中, 提高完成真实环境中任务的性能.域适应在纯视觉领域应用很多, 结合机器人学习也有一些值得关注的工作[112, 113].基于模型的强化学习算法可辅助机器人虚拟到现实的迁移.Christiano等[114]学习一个逆向动力学模型, 决定真实机器人执行什么样的动作会更容易实现虚拟环境中下一时刻的状态, 以此实现迁移.Nagabandi等[115]利用元学习(Meta-Lear-ning)训练动力学模型先验, 再结合最新数据快速学习环境模型, 实现快速迁移.

5.2 在机器人领域的挑战

目前基于模型的强化学习也存在一些不足.首先, 模型存在不确定性和近似误差, 虽然有很多工作缓解这个问题, 然而大多都是针对虚拟环境, 而真实的机器人环境更复杂, 因此对模型要求更高, 如何在真实环境中减小模型误差是一个问题.其次, 基于模型的强化学习的渐进性能不如无模型的强化学习, 这是限制其应用的一个原因, 因此利用MBRL的高样本效率的同时需要设法达到MFRL的高渐进性能.针对视觉输入, 潜在动力学模型是一个有效方法, 但是通常需要学习一个表示, 如何结合先验知识学习一个更好的表示也是未来值得研究的方向.此外, 考虑安全问题和采样效率, 机器人学习适合先在虚拟环境中训练再迁移到真实世界, 这方面的研究可考虑集成迁移学习中域随机化和域适应的方法, 是未来研究方向的一个重点.最后, 基于模型的强化学习通常有更多的超参数和网络模型, 可能存在计算量较大、不稳定的问题, 这个问题可能无法避免, 需要在算法研究中尽量设法减轻.针对这些问题, 基于模型的强化学习还有很大的研究空间.

6 结束语

机器人学习作为人工智能领域的研究热点, 受到研究者们的广泛关注.强化学习由于适合解决决策问题, 因此被视为解决机器人学习的一种有效方法, 而基于模型的强化学习(MBRL)存在许多优点, 更接近人类的学习方式, 也更适合机器人学习.本文首先介绍机器人学习的形式化.然后, 介绍基于模型的强化学习算法的基础理论, 详细论述当前MBRL中模型的学习和模型的利用.最后, 基于MBRL的优点介绍其在机器人学习中的应用, 并展望MBRL未来的研究方向.随着基于模型的强化学习的发展, 其在机器人学习中存在的问题会逐一解决, 机器人也将更多地出现在工程和生活之中.

参考文献
[1] OSA T, PAJARINEN J, NEUMANN G, et al. An Algorithmic Perspective on Imitation Learning. Foundations and Trends® in Robo-tics, 2018, 7(1/2): 1-179. [本文引用:1]
[2] SUTTON R S, BARTO A G. Reinforcement Learning: An Introduction. Cambridge, USA: The MIT Press, 1998. [本文引用:3]
[3] AKKAYA I, ANDRYCHOWICZ M, CHOCIEJ M, et al. Solving Rubik's Cube with a Robot Hand [C/OL]. [2021-12-26]. https://arxiv.org/pdf/1910.07113.pdf. [本文引用:2]
[4] LEVINE S, FINN C, DARRELL T, et al. End-to-End Training of Deep Visuomotor Policies. Journal of Machine Learning Research, 2016, 17(1): 1334-1373. [本文引用:6]
[5] FAZELI N, OLLER M, WU J, et al. See, Feel, Act: Hierarchical Learning for Complex Manipulation Skills with Multisensory Fusion. Science Robotics, 2019, 4(26). DOI: DOI:10.1126/scirobotics.aav3123. [本文引用:1]
[6] FISAC J F, AKAMETALU A K, ZEILINGER M N, et al. A Gene-ral Safety Framework for Learning-Based Control in Uncertain Robotic Systems. IEEE Transactions on Automatic Control, 2019, 64(7): 2737-2752. [本文引用:1]
[7] KROEMER O, NIEKUM S, KONIDARIS G. A Review of Robot Learning for Manipulation: Challenges, Representations, and Algorithms. Journal of Machine Learning Research, 2021, 22: 1-82. [本文引用:2]
[8] BELLMAN R. On the Theory of Dynamic Programming. Proceedings of the National Academy of Sciences of the United States of America, 1952, 38(8): 716-719. [本文引用:1]
[9] MOERLAND T M, BROEKENS J, JONKER C M. Model-Based Reinforcement Learning: A Survey[C/OL]. [2021-12-26]. https://arxiv.org/pdf/2006.16712v3.pdf. [本文引用:2]
[10] SILVER D, SCHRITTWIESER J, SIMONYAN K, et al. Mastering the Game of Go without Human Knowledge. Nature, 2017, 550(7676): 354-359. [本文引用:1]
[11] SUTTON R S. Dyna, An Integrated Architecture for Learning, Pla-nning, and Reacting. ACM SIGART Bulletin, 1991, 2(4): 160-163. [本文引用:2]
[12] SUTTON R S. Planning by Incremental Dynamic Programming // Proc of the 8th International Conference on Machine Learning. San Diego, USA: JMLR, 1991: 353-357. [本文引用:1]
[13] SUTTON R S, SZEPESVÁRI C, GERAMIFARD A, et al. Dyna-Style Planning with Linear Function Approximation and Prioritized Sweeping // Proc of the 24th Conference on Uncertainty in Artificial Intelligence. New York, USA: ACM, 2008: 528-536. [本文引用:1]
[14] PARR R, LI L H, TAYLOR G, et al. An Analysis of Linear Mo-dels, Linear Value-Function Approximation, and Feature Selection for Reinforcement Learning // Proc of the 25th International Con-ference on Machine learning. San Diego, USA: JMLR, 2008: 752-759. [本文引用:1]
[15] HESTER T, STONE P. Learning and Using Models // WIERING M, VAN OTTERLO M, eds. Reinforcement Learning. Berlin, Ger-many: Springer, 2012: 111-141 [本文引用:1]
[16] JONG N K, STONE P. Model-Based Function Approximation in Reinforcement Learning // Proc of the 6th International Joint Conference on Autonomous Agents and Multiagent Systems. New York, USA: ACM, 2007: 1-8. [本文引用:1]
[17] HESTER T, STONE P. TEXPLORE: Real-Time Sample-Efficient Reinforcement Learning for Robots. Machine Learning, 2013, 90: 385-429. [本文引用:1]
[18] MÜLLER K R, SMOLA A J, RÄTSCH G, et al. Predicting Time Series with Support Vector Machines // Proc of the International Conference on Artificial Neural Networks. Berlin, Germany: Springer, 1997: 999-1004. [本文引用:1]
[19] FU J, LEVINE S, ABBEEL P. One-Shot Learning of Manipulation Skills with Online Dynamics Adaptation and Neural Network Priors // Proc of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington, USA: IEEE, 2016: 4019-4026. [本文引用:1]
[20] WAHLSTRÖM N, SCHÖN T B, DEISENROTH M P. From Pixels to Torques: Policy Learning with Deep Dynamical Models[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1502.02251v2.pdf. [本文引用:1]
[21] DEISENROTH M P, FOX D, RASMUSSEN C E. Gaussian Pro-cesses for Data-Efficient Learning in Robotics and Control. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(2): 408-423. [本文引用:3]
[22] KOPICKI M, ZUREK S, STOLKIN R, et al. Learning Modular and Transferable Forward Models of the Motions of Push Manipulated Objects. Autonomous Robots, 2017, 41(5): 1061-1082. [本文引用:2]
[23] LIN L J. Self-Improving Reactive Agents Based on Reinforcement Learning, Planning and Teaching. Machine Learning, 1992, 8: 293-321. [本文引用:1]
[24] VAN HASSELT H P, HESSEL M, ASLANIDES J. When to Use Parametric Models in Reinforcement Learning? // Proc of the 33rd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2019: 14345-14356. [本文引用:1]
[25] DER KIUREGHIAN A, DITLEVSEN O. Aleatory or Epistemic? Does It Matter? Structural Safety, 2009, 31(2): 105-112. [本文引用:1]
[26] LANG T, TOUSSAINT M, KERSTING K. Exploration in Relatio-nal Domains for Model-Based Reinforcement Learning. Journal of Machine Learning Research, 2012, 13: 3725-3768. [本文引用:1]
[27] MOERLAND T M, BROEKENS J, JONKER C M. Learning Multimodal Transition Dynamics for Model-Based Reinforcement Lear-ning[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1705.00470.pdf. [本文引用:1]
[28] SCHOLZ J, LEVIHN M, ISBELL C, et al. A Physics-Based Mo-del Prior for Object-Oriented MDPs. Proceedings of Machine Lear-ning Research, 2014, 32(2): 1089-1097. [本文引用:1]
[29] HÖGMAN V, BJÖRKMAN M, MAKI A, et al. A Sensorimotor Learning Framework for Object Categorization. IEEE Transactions on Cognitive and Developmental Systems, 2016, 8(1): 15-25. [本文引用:1]
[30] DEISENROTH M P, RASMUSSEN C E. PILCO: A Model-Based and Data-Efficient Approach to Policy Search // Proc of the 28th International Conference on Machine Learning. San Diego, USA: JMLR, 2011: 465-472. [本文引用:2]
[31] GAL Y, MCALLISTER R T, RASMUSSEN C E. Improving PILCO with Bayesian Neural Network Dynamics Models[C/OL]. [2021-12-26]. http://mlg.eng.cam.ac.uk/yarin/PDFs/DeepPILCO.pdf. [本文引用:1]
[32] KURUTACH T, CLAVERA I, DUAN Y, et al. Model-Ensemble Trust-Region Policy Optimization[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1802.10592v1.pdf. [本文引用:3]
[33] KE N R, SINGH A, TOUATI A, et al. Learning Dynamics Model in Reinforcement Learning by Incorporating the Long Term Future[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1903.01599v2.pdf. [本文引用:1]
[34] VENKATRAMAN A, HEBERT M, BAGNELL J A. Improving Multi-step Prediction of Learned Time Series Models // Proc of the 29th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI, 2015: 3024-3030. [本文引用:1]
[35] ABBEEL P, NG A Y. Learning First-Order Markov Models for Control[C/OL]. [2021-12-26]. http://ai.stanford.edu/~ang/papers/nips04-controlmodel.pdf. [本文引用:1]
[36] ASADI K, CATER E, MISRA D, et al. Towards a Simple Approach to Multi-step Model-Based Reinforcement Learning[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1811.00128.pdf. [本文引用:1]
[37] MISHRA N, ABBEEL P, MORDATCH I. Prediction and Control with Temporal Segment Models // Proc of the 34th International Conference on Machine Learning. San Diego, USA: JMLR, 2017: 2459-2468. [本文引用:1]
[38] FINN C, GOODFELLOW I, LEVINE S. Unsupervised Learning for Physical Interaction through Video Prediction // Proc of the 30th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2016: 64-72 [本文引用:2]
[39] FINN C, LEVINE S. Deep Visual Foresight for Planning Robot Motion // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2017: 2786-2793. [本文引用:3]
[40] EBERT F, FINN C, DASARI S, et al. Visual Foresight: Model-Based Deep Reinforcement Learning for Vision-Based Robotic Control[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1812.00568.pdf. [本文引用:1]
[41] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-Level Control through Deep Reinforcement Learning. Nature, 2015, 518(7540): 529-533. [本文引用:1]
[42] VAN HASSELT H, GUEZ A, SILVER D. Deep Reinforcement Learning with Double Q-Learning // Proc of the 30th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI, 2016: 2094-2100. [本文引用:1]
[43] WANG Z Y, SCHAUL T, HESSEL M, et al. Dueling Network Architectures for Deep Reinforcement Learning[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1511.06581.pdf. [本文引用:1]
[44] HAUSKNECHT M, STONE P. Deep Recurrent Q-Learning for Partially Observable MDPs[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1507.06527v4.pdf. [本文引用:1]
[45] BELLEMARE M G, DABNEY W, MUNOS R. A Distributional Perspective on Reinforcement Learning[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1707.06887.pdf. [本文引用:1]
[46] SCHAUL T, QUAN J, ANTONOGLOU I, et al. Prioritized Experience Replay[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1511.05952.pdf. [本文引用:1]
[47] FORTUNATO M, AZAR M G, PIOT B, et al. Noisy Networks for Exploration[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1706.10295.pdf. [本文引用:1]
[48] HESSEL M, MODAYIL J, VAN HASSELT H, et al. Rainbow: Combining Improvements in Deep Reinforcement Learning // Proc of the 32nd AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI, 2018: 3215-3222. [本文引用:1]
[49] KINGMA D P, WELLING M. Auto-Encoding Variational Bayes[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1312.6114v10.pdf. [本文引用:1]
[50] WATTER M, SPRINGENBERG J T, BOEDECKER J, et al. Embed to Control: A Locally Linear Latent Dynamics Model for Control from Raw Images[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1506.07365.pdf. [本文引用:4]
[51] ZHANG M, VIKRAM S, SMITH L, et al. SOLAR: Deep Structured Representations for Model-Based Reinforcement Learning. Proceedings of Machine Learning Research, 2019, 97: 7444-7453. [本文引用:4]
[52] HA D, SCHMIDHUBER J. World Models[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1803.10122.pdf. [本文引用:1]
[53] DIUK C, COHEN A, LITTMAN M L. An Object-Oriented Representation for Efficient Reinforcement Learning // Proc of the 25th International Conference on Machine Learning. San Diego, USA: JMLR, 2008: 240-247. [本文引用:1]
[54] FRAGKIADAKI K, AGRAWAL P, LEVINE S, et al. Learning Visual Predictive Models of Physics for Playing Billiards[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1511.07404.pdf. [本文引用:1]
[55] KANSKY K, SILVER T, MÉLY D A, et al. Schema Networks: Zero-Shot Transfer with a Generative Causal Model of Intuitive Physics // Proc of the 34th International Conference on Machine Learning. San Diego, USA: JMLR, 2017: 1809-1818. [本文引用:1]
[56] VAN STEENKISTE S, CHANG M, GREFF K, et al. Relational Neural Expectation Maximization: Unsupervised Discovery of Objects and Their Interactions[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1802.10353v1.pdf. [本文引用:1]
[57] BATTAGLIA P W, PASCANU R, LAI M, et al. Interaction Networks for Learning about Objects, Relations and Physics[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1612.00222.pdf. [本文引用:1]
[58] KIPF T, VAN DER POL E, WELLING M. Contrastive Learning of Structured World Models[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1911.12247.pdf. [本文引用:2]
[59] WATTERS N, MATTHEY L, BOSNJAK M, et al. Cobra: Data-Efficient Model-Based Rl through Unsupervised Object Discovery and Curiosity-Driven Exploration[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1905.09275v1.pdf. [本文引用:1]
[60] BURGESS C P, MATTHEY L, WATTERS N, et al. MONet: Un-supervised Scene Decomposition and Representation[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1901.11390.pdf. [本文引用:1]
[61] VEERAPANENI R, CO-REYES J D, CHANG M, et al. Entity Abstraction in Visual Model-Based Reinforcement Learning. Proceedings of Machine Learning Research, 2020, 100: 1439-1456. [本文引用:1]
[62] MA X, CHEN S W, HSU D, et al. Contrastive Variational Reinforcement Learning for Complex Observations. Proceedings of Machine Learning Research, 2021, 155: 959-972. [本文引用:1]
[63] SERMANET P, LYNCH C, CHEBOTAR Y, et al. Time-Contrastive Networks: Self-Supervised Learning from Video // Proc of the IEEE International Conference on Robotics and Automation. Wa-shington, USA: IEEE, 2018: 1134-1141. [本文引用:1]
[64] GHOSH D, GUPTA A, LEVINE S. Learning Actionable Representations with Goal-Conditioned Policies[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1811.07819.pdf. [本文引用:1]
[65] JONSCHKOWSKI R, BROCK O. Learning State Representations with Robotic Priors. Autonomous Robots, 2015, 39(3): 407-428. [本文引用:1]
[66] PATHAK D, AGRAWAL P, EFROS A A, et al. Curiosity-Driven Exploration by Self-Supervised Prediction // Proc of the 34th International Conference on Machine Learning. San Diego, USA: JMLR, 2017: 2778-2787. [本文引用:1]
[67] AGRAWAL P, NAIR A, ABBEEL P, et al. Learning to Poke by Poking: Experiential Learning of Intuitive Physics[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1606.07419.pdf. [本文引用:1]
[68] SHELHAMER E, MAHMOUDIEH P, ARGUS M, et al. Loss Is Its Own Reward: Self-Supervision for Reinforcement Learning[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1612.07307v1.pdf. [本文引用:1]
[69] ZHANG A, SATIJA H, PINEAU J. Decoupling Dynamics and Reward for Transfer Learning[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1804.10689.pdf. [本文引用:1]
[70] SAWADA Y. Disentangling Controllable and Uncontrollable Fac-tors of Variation by Interacting with the World[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1804.06955v2.pdf. [本文引用:1]
[71] THOMAS V, BENGIO E, FEDUS W, et al. Disentangling the Independently Controllable Factors of Variation by Interacting with the World[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1802.09484.pdf. [本文引用:1]
[72] CHOI J, GUO Y J, MOCZULSKI M, et al. Contingency-Aware Exploration in Reinforcement Learning[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1811.01483.pdf. [本文引用:1]
[73] GRIMM C, BARRETO A, SINGH S, et al. The Value Equivalence Principle for Model-Based Reinforcement Learning[C/OL]. [2021-12-26]. https://arxiv.org/pdf/2011.03506.pdf. [本文引用:1]
[74] GRIMM C, BARRETO A, FARQUHAR G, et al. Proper Value Equivalence[C/OL]. [2021-12-26]. https://arxiv.org/pdf/2106.10316v1.pdf. [本文引用:1]
[75] FARQUHAR G, BAUMLI K, MARINHO Z, et al. Self-Consistent Models and Values[C/OL]. [2021-12-26]. https://arxiv.org/pdf/2110.12840.pdf. [本文引用:1]
[76] SCHRITTWIESER J, ANTONOGLOU I, HUBERT T, et al. Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model. Nature, 2020, 588(7839): 604-609. [本文引用:1]
[77] SILVER D, VAN HASSELT H, HESSEL M, et al. The Predictron: End-to-End Learning and Planning. Proceedings of Machine Learning Research, 2017, 70: 3191-3199. [本文引用:1]
[78] OH J, SINGH S, LEE H. Value Prediction Network[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1707.03497.pdf. [本文引用:1]
[79] LENZ I, KNEPPER R, SAXENA A. DeepMPC: Learning Deep Latent Features for Model Predictive Control[C/OL]. [2021-12-26]. http://www.roboticsproceedings.org/rss11/p12.pdf. [本文引用:1]
[80] HUBER A, GERDTS M. A Dynamic Programming MPC Approach for Automatic Driving along Tracks and Its Realization with Online Steering Controllers. IFAC-PapersOnLine, 2017, 50(1): 8686-8691. [本文引用:1]
[81] ZHANG T H, KAHN G, LEVINE S, et al. Learning Deep Control Policies for Autonomous Aerial Vehicles with MPC-Guided Policy Search // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2016: 528-535. [本文引用:1]
[82] HAFNER D, LILLICRAP T, FISCHER I, et al. Learning Latent Dynamics for Planning from Pixels // Proceedings of the 36th International Conference on Machine Learning. San Diego, USA: JMLR, 2019: 2555-2565. [本文引用:1]
[83] VOLPI N C, WU Y, OGNIBENE D. Towards Event-Based MCTS for Autonomous Cars // Proc of the AFSIPA Annual Summit and Conference. Washington, USA: IEEE, 2017: 420-427. [本文引用:1]
[84] HESTER T, QUINLAN M, STONE P. RTMBA: A Real-Time Model-Based Reinforcement Learning Architecture for Robot Control // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2012: 85-90. [本文引用:1]
[85] LEVINE S, KOLTUN V. Guided Policy Search[C/OL]. [2021-12-26]. http://proceedings.mlr.press/v28/levine13.pdf. [本文引用:2]
[86] LEVINE S, ABBEEL P. Learning Neural Network Policies with Guided Policy Search under Unknown Dynamics // Proc of the 27th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2014, I: 1071-1079. [本文引用:2]
[87] KALWEIT G, BOEDECKER J. Uncertainty-Driven Imagination for Continuous Deep Reinforcement Learning. Proceedings of Machine Learning Research, 2017, 78: 195-206. [本文引用:1]
[88] GU S X, LILLICRAP T, SUTSKEVER I, et al. Continuous Deep Q-Learning with Model-Based Acceleration // Proc of the 33rd International Conference on Machine Learning. San Diego, USA: JMLR, 2016: 2829-2838. [本文引用:1]
[89] FEINBERG V, WAN A, STOICA I, et al. Model-Based Value Estimation for Efficient Model-Free Reinforcement Learning[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1803.00101v1.pdf. [本文引用:1]
[90] BUCKMAN J, HAFNER D, TUCKER G, et al. Sample-Efficient Reinforcement Learning with Stochastic Ensemble Value Expansion // Proc of the 32nd Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2018: 8224-8234. [本文引用:1]
[91] LUO Y P, XU H Z, LI Y Z, et al. Algorithmic Framework for Model-Based Deep Reinforcement Learning with Theoretical Gua-rantees[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1807.03858v3.pdf. [本文引用:1]
[92] JANNER M, FU J, ZHANG M, et al. When to Trust Your Model: Model-Based Policy Optimization[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1906.08253v2.pdf. [本文引用:1]
[93] LAI H, SHEN J, ZHANG W N, et al. Bidirectional Model-Based Policy Optimization[C/OL]. [2021-12-26]. https://arxiv.org/pdf/2007.01995.pdf. [本文引用:1]
[94] HEESS N, WAYNE G, SILVER D, et al. Learning Continuous Control Policies by Stochastic Value Gradients // Proc of the 28th International Conference on Neural Information Processing Sys-tems. Cambridge, USA: The MIT Press, 2015, II: 2944-2952. [本文引用:1]
[95] CLAVERA I, FU V, ABBEEL P. Model-Augmented Actor-Critic: Backpropagating through Paths[C/OL]. [2021-12-26]. https://arxiv.org/pdf/2005.08068.pdf. [本文引用:1]
[96] HAFNER D, LILLICRAP T, BA J, et al. Dream to Control: Learning Behaviors by Latent Imagination[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1912.01603v1.pdf. [本文引用:1]
[97] TAMAR A, LEVINE S, ABBEEL P, et al. Value Iteration Networks[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1602.02867v1.pdf. [本文引用:1]
[98] SRINIVAS A, JABRI A, ABBEEL P, et al. Universal Planning Networks: Learning Generalizable Representations for Visuomotor Control. Proceedings of Machine Learning Research, 2018, 80: 4732-4741. [本文引用:1]
[99] KARKUS P, HSU D, LEE W S. QMDP-Net: Deep Learning for Planning under Partial Observability[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1703.06692.pdf. [本文引用:1]
[100] GUEZ A, WEBER T, ANTONOGLOU I, et al. Learning to Search with MCTSnets[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1802.04697.pdf. [本文引用:1]
[101] RACANIÈRE S, WEBER T, REICHERT D P, et al. Imagination-Augmented Agents for Deep Reinforcement Learning // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2017: 5694-5705. [本文引用:1]
[102] PASCANU R, LI Y J, VINYALS O, et al. Learning Model-Based Planning from Scratch[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1707.06170v1.pdf. [本文引用:1]
[103] NAIR A, PONG V, DALAL M, et al. Visual Reinforcement Lear-ning with Imagined Goals[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1807.04742v2.pdf. [本文引用:2]
[104] LOWREY K, RAJESWARAN A, KAKADE S, et al. Plan Online, Learn Offline: Efficient Learning and Exploration via Model-Based Control[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1811.01848v1.pdf. [本文引用:1]
[105] TODOROV E, EREZ T, TASSA Y. MuJoCo: A Physics Engine for Model-Based Control // Proc of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington, USA: IEEE, 2012: 5026-5033. [本文引用:2]
[106] SEKAR R, RYBKIN O, DANIILIDIS K, et al. Planning to Explore via Self-Supervised World Models[C/OL]. [2021-12-26]. https://arxiv.org/pdf/2005.05960.pdf. [本文引用:1]
[107] ANDRYCHOWICZ M, WOLSKI F, RAY A, et al. Hindsight Experience Replay[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1707.01495v1.pdf. [本文引用:1]
[108] KOENIG N, HOWARD A. Design and Use Paradigms for Gazebo, an Open-Source Multi-robot Simulator // Proc of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington, USA: IEEE, 2004, III: 2149-2154. [本文引用:1]
[109] TOBIN J, FONG R, RAY A, et al. Domain Rand omization for Transferring Deep Neural Networks from Simulation to the Real World // Proc of the IEEE/RSJ International Conference on Inte-lligent Robots and Systems. Washington, USA: IEEE, 2017: 23-30. [本文引用:1]
[110] PENG X B, ANDRYCHOWICZ M, ZAREMBA W, et al. Sim-to-Real Transfer of Robotic Control with Dynamics Rand omization // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2018: 3803-3810. [本文引用:1]
[111] ANDRYCHOWICZ O A I M, BAKER B, CHOCIEJ M, et al. Learning Dexterous In-Hand Manipulation. International Journal of Robotics Research, 2020, 39(1): 3-20. [本文引用:1]
[112] BOUSMALIS K, IRPAN A, WOHLHART P, et al. Using Simu-lation and Domain Adaptation to Improve Efficiency of Deep Robotic Grasping // Proc of the IEEE International Conference on Robotics and Automation. Washington, USA: IEEE, 2018: 4243-4250. [本文引用:1]
[113] JAMES S, WOHLHART P, KALAKRISHNAN M, et al. Sim-to-Real via Sim-to-Sim: Data-Efficient Robotic Grasping via Rand omized-to-Canonical Adaptation Networks // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 12627-12637. [本文引用:1]
[114] CHRISTIANO P, SHAH Z, MORDATCH I, et al. Transfer from Simulation to Real World through Learning Deep Inverse Dyna-mics Model[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1610.03518v1.pdf. [本文引用:1]
[115] NAGABANDI A, CLAVERA I, LIU S M, et al. Learning to Adapt in Dynamic, Real-World Environments through Meta-Reinforcement Learning[C/OL]. [2021-12-26]. https://arxiv.org/pdf/1803.11347v6.pdf. [本文引用:1]