引用本文
关伟凡, 张希. 基于噪声对比估计的权重自适应对抗生成式模仿学习. 模式识别与人工智能, 2023,36(4): 300-312
GUAN Weifan, ZHANG Xi. Weight Adaptive Generative Adversarial Imitation Learning Based on Noise Contrastive Estimation. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(4): 300-312.  
Doi: 10.16451/j.cnki.issn1003-6059.202304002
Permissions
Copyright©2023, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于噪声对比估计的权重自适应对抗生成式模仿学习
关伟凡1,2, 张希1
1.中国科学院自动化研究所 模式识别国家重点实验室 北京 100190
2.中国科学院大学 人工智能学院 北京 100049
通信作者：

张 希,博士,副教授,主要研究方向为机器学习、强化学习.E-mail:xi.zhang@ia.ac.cn.

作者简介：

关伟凡,硕士研究生,主要研究方向为强化学习、模仿学习.E-mail:guanweifan2020@ia.ac.cn.

收稿日期: 2022-11-25 接受日期: 2023-04-11
资助项目: 科技创新2030——“新一代人工智能”重大项目(No.2020AAA0103400)资助
摘要

传统模仿学习需满足专家样本均为质量极高的最优专家样本,这一限制条件既提高数据的采集难度也限制算法的应用场景.由此,文中提出基于噪声对比估计的权重自适应对抗生成式模仿学习算法(Weight Adaptive Generative Adversarial Imitation Learning Based on Noise Contrastive Estimation, GLANCE),在专家样本质量不一致的任务场景下可保持较高性能.首先,使用噪声对比估计训练特征提取器,改善次优专家样本特征分布.然后,为专家样本设定可学习权重系数,并对基于权重系数重分布后的样本执行对抗生成式模仿学习.最后,基于已知相对排序的评估数据计算排序损失,通过梯度下降法优化权重系数,改善数据分布.在多个连续控制型任务上的实验表明,专家样本质量不一致时,GLANCE仅需要获取专家样本数据集上5%数据作为评估数据集,就可以达到较优的性能表现.

关键词: 强化学习; 模仿学习; 噪声对比估计; 自适应权重
中图分类号:TP 18
Weight Adaptive Generative Adversarial Imitation Learning Based on Noise Contrastive Estimation
GUAN Weifan1,2, ZHANG Xi1
1. National Laboratory of Pattern Recognition, Institute of Automation, Chinese Academy of Sciences, Beijing 100190
2. School of Artificial Intelligence, University of Chinese Academy of Sciences, Beijing 100049
Corresponding author:
ZHANG Xi, Ph.D., associate professor. Her research interests include machine learning and reinforcement lear-ning.

About Author:
GUAN Weifan, master student. His research interests include reinforcement lear-ning and imitation learning.

Fund:National Key Research and Development Program of China(No.2020AAA0103400)
Abstract

The traditional imitation learning requires expert demonstrations of extremely high quality. This restriction not only increases the difficulty of data collection but also limits application scenarios of algorithms. To address this problem, weight adaptive generative adversarial imitation learning based on noise contrastive estimation(GLANCE) is proposed to maintain high performance in scenarios where the quality of expert demonstration is inconsistent. Firstly, a feature extractor is trained by noise contrastive estimation to improve the feature distribution of suboptimal expert demonstrations. Then, weight coefficients are set for the expert demonstrations, and generative adversarial imitation learning is performed on the expert demonstrations after redistribution based on the weight coefficients. Finally, ranking loss is calculated based on the known relative ranking evaluation data and weight coefficients are optimized through gradient descent to improve the data distribution. Experiments on multiple continuous control tasks show that GLANCE only needs to obtain 5% of the expert demonstrations dataset as evaluation data to achieve superior performance while the quality of the expert demonstration is inconsistent.

Key words: Reinforcement Learning; Imitation Learning; Noise Contrastive Estimation; Adaptive Weight

模仿学习(Imitation Learning, IL)[1]旨在从人类专家执行目标任务产生的数据中进行信息挖掘, 进而学习到接近甚至超越人类专家策略的新策略.模仿学习可以改善强化学习(Reinforcement Lear-ning, RL)[2]采样效率较低、奖励函数难以设计等弊病, 因此受到学术界和工业界的广泛关注.近年来不断涌现出多种模仿学习相关算法, 主要类别有基于监督学习的行为克隆[3, 4, 5, 6]和基于对抗生成学习的逆强化学习[7, 8, 9, 10, 11]等.

目前, 模仿学习正在拓展到更复杂且更具挑战性的应用场景.Peng等[12]提出DeepMimic, 尝试对跳跃、空翻甚至武术等复杂的精密动作进行高质量还原.基于YouTube视频, Standford团队让机械臂学习抓取任务[13, 14, 15], 尝试从海量的无监督视频信息中直接学习行为动作.T-REX(Trajectory-Ranked Re-ward Extrapolation)[16]、D-REX(Disturbance-Based Reward Extrapolation)[17]、CAIL(Confidence-Aware Imitation Learning)[10]等尝试引入先验信息, 使模仿学习算法的性能超越被模仿的专家策略.若上述技术能够取得持续突破, 未来的模仿学习将有可能在海量无监督视频数据下模仿复杂动作行为, 达到超越被模仿者的性能表现.

逆强化学习(Inverse RL, IRL)[8]为模仿学习重要的研究方向之一.IRL的目的是从智能体的行动中推断出最优的奖励函数, 代替人工设计的奖励函数.区别于行为克隆对专家策略的单纯模仿, IRL不断挖掘专家样本的隐含信息, 学习到的奖励函数在应对环境变化时具有更好的泛化性和鲁棒性.

传统的模仿学习算法假设专家样本均为最优专家样本, 未针对专家样本的品质进行区分.这种做法具有明显的局限性:一方面, 在很多任务场景下, 出于人工成本的限制, 无法获取足够的最优专家样本供模仿学习智能体得到充分的训练, 这种情况下必须依赖于从次优专家样本中获取信息.另一方面, 算法性能过于依赖样本数据的品质, 一旦专家数据集上含有次优专家样本, 对这类数据的直接模仿将使算法性能大打折扣.因此, 研究混合专家样本建模, 是提升模仿学习数据利用效率并最终提升算法性能亟待解决的问题.

目前学者们还提出一些针对混合专家样本任务场景的IRL相关工作.Chen等[18]提出SSRR(Self-Supervised Reward Regression), 通过IRL得到初始策略和奖励函数, 再向初始策略网络注入不同振幅的噪声, 形成带有噪声的专家样本, 最后利用噪声专家样本学习奖励函数, 并将学习到的奖励函数投放到前向强化学习中使用.Wu等[11]提出2IWIL(Two-Step Importance Weighting IL), 利用少量预先标注权重系数的专家样本训练预测器, 并通过该预测器预测大量无监督数据的权重系数, 再将权重系数重分布后的专家样本投入模仿学习的训练.Wu等[11]同时提出IC-GAIL(Generative Adversarial IL with Imperfect Demonstration and Confidence)[11], 他们认为2IWIL可能出现累计误差的问题, 在2IWIL的基础上, IC-GAIL以端到端的方式训练, 通过占有率度量匹配, 使策略分布接近最优策略分布.Zhang等[10]提出CAIL, 为专家样本设定初始权重系数, 并基于当前模仿学到的策略性能自适应地调整权重系数, 通过双重循环的交替式优化, 改善样本分布.Xu等[19]提出DWBC(Discriminator-Weighted Behavioral Cloning), 结合对抗生成式网络和行为克隆, 以分辨专家样本和非专家样本这一任务训练判别器, 并以收敛后判别器的输出结果作为权重系数, 计算行为克隆损失, 优化策略参数.Beliaev等[20]提出ILEED(Imitation Learning by Estimating Expertise of Demonstrators), 通过编码器将状态映射到隐空间, 在隐空间内计算专家样本和非专家样本的相似度系数, 并将其作为非专家样本的权重系数, 参与行为克隆的损失计算.

然而, 上述方法均依赖对专家样本进行预处理以获取相对排序或真实奖励等先验知识, 耗费大量人工标注成本.针对上述问题, 本文提出基于噪声对比估计的权重自适应对抗生成式模仿学习算法(Weight Adaptive Generative Adversarial Imitation Learning Based on Noise Contrastive Estimation, GLANCE), 仅需要获取专家样本数据集上5%数据的相对排序作为评估数据集, 就可以达到甚至超越同类算法的性能表现, 在提升性能的同时大幅节省标注数据的人力成本.GLANCE使用噪声对比估计对特征提取器进行预训练.对比次优专家样本和最优专家样本的行为特征, 使用噪声信号模拟两者之间的差距, 从而训练出更鲁棒的特征提取器.通过这种方法, 次优专家样本特征提取后的隐含状态将更接近最优专家样本的状态表征, 规避次优专家样本对算法性能的影响.同时以预测排序损失作为优化目标, 通过梯度下降法对权重系数进行更新, 使混合专家样本的数据分布尽可能接近最优策略的样本分布, 使算法在优化过程中更加关注最优专家样本, 提升算法性能.

1 相关知识
1.1 强化学习

强化学习(RL)[2]通过与周围环境互动, 并尝试根据周围环境反馈的奖励学习最佳的行动策略, 进而达到累计奖励最大化的目的.将强化学习问题建模成马尔可夫决策过程(Markov Decision Process, MDP), 由智能体(Agent)、环境(Environment)、状态(State)、动作(Action)、奖励(Reward)及状态转移概率(State Transition Probability)组成.MDP的数学形式可写成如下六元组:

M=< S, A, T, R, ρ 0, γ > ,

其中, S表示状态空间, A表示动作空间, T表示状态转移概率, R表示奖励函数, ρ 0表示初始状态分布, γ 表示奖励的衰减系数.策略π ∶ S× A→ [0, 1]定义为给定状态下, 动作空间中动作的概率分布.

智能体连续与环境进行决策交互, 使用累计期望回报评估策略的性能表现, 表达式为

η π = Es0~ρ0, π[ ∑t=0+∞γ tR(st, at)].

强化学习算法的最终目标为寻得最优策略, 即能最大化累计期望回报的策略.

1.2 模仿学习

相比强化学习, 模仿学习[1]从专家策略π d产生的专家样本{ξ 1, ξ 2, …, ξ k}中学习专家的决策规律.从专家样本中自适应地学习奖励函数, 摆脱对人工设计奖励函数的依赖, 并且从在线交互式学习转向离线数据驱动式学习, 提高采样效率和学习速率.每条专家样本为一条状态动作对序列

ξ i={s0, a0, s1, a1, …, sn, an},

期望回报为

η ξ = ∑t=0nγ tR(st, at).

定义占有率度量(Occupancy Measure)[8], ρ π 为策略π 在和环境交互过程中访问的状态动作对数据分布, 则

ρπ:S×A→R:ρπs, a=πas∑t=0∞γtPst=sπ

模仿学习的目标可以描述为:使当前策略的占有率度量尽可能接近被模仿的专家策略的占有率度量, 从而在相同环境状态下, 当前策略的动作决策接近专家策略的动作决策, 进而达到模仿专家行为的目的.选用相对熵(Relative Entropy), 即KL散度度量两个分布之间的距离, 则模仿学习的优化目标可写为

arg minπKL( ρπd‖ ρ π )=arg minπ∑ ρπdlog( ρπdρπ),

其中, ρπd表示专家策略的占有率度量, ρ π 表示当前策略的占有率度量.

1.3 对抗生成式模仿学习

对抗生成网络(Generative Adversarial Net-work, GAN)[21]是一种主流的生成式模型, 核心由两部分组成:生成器G与判别器D.

GAN的优化目标可写作

$\begin{aligned}V(D, G)= & E_{x \sim p_{\mathrm{data}}}[\log D(x)]+ \\& E_{z \sim p_{z}}[\log (1-D(G(z)))],\end{aligned}$

其中, pdata表示真实样本分布, p(z)表示噪声分布.优化目标V(D, G)值越高表示判别结果越准确.

生成器通过最小化优化目标达到由噪声信号生成近似真实样本的仿真样本的目的, 而判别器通过最大化优化目标以精确分辨真实样本和仿真样本, 故GAN对抗训练的优化目标为:

minGmaxDV(D, G)= Ex~pdatalog D(x)]+ Ez~pzlog(1-D(x))].

GAN通过对抗训练的方式, 不断减小仿真样本和真实样本分布的KL散度, 达到生成类似真实样本的仿真样本的目的.

受GAN启发, GAIL(Generative Adversarial Imitation Learning)[8]通过对抗训练的方式减小当前策略和专家策略的占有率度量的KL散度, 从而使当前策略模仿专家策略的决策行为.GAIL的优化目标如下:

minπmaxRV(R, π )= Es, a~πd[log R(s, a)]+Es', a'~π [log(1-R(s', a'))],

其中, π 表示当前策略, π d表示被模仿的专家策略, 奖励函数R充当判别器.

2 基于噪声对比估计的权重自适应对抗生成式模仿学习

在实际场景中, 为了保证数据规模及收集效率, 专家数据往往由多个不同的专家策略 πid产生, i=1, 2, …, n.其中必有策略产生样本的累计期望回报优于其它策略, 本文称为最优策略π * , 从最优策略中产生的专家样本即视为最优专家样本, 而其余样本称为次优专家样本.

本文针对混合专家样本数据集上模仿学习算法性能损失问题, 提出基于噪声对比估计的权重自适应对抗生成式模仿学习算法(GLANCE).

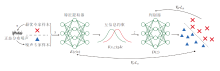
GLANCE流程如图1所示.算法主体分为两部分.1)特征提取器的训练.利用最优专家样本及噪声专家样本进行噪声对比估计, 得到具有特征选择作用的特征提取器, 使次优专家样本的状态表征更接近最优专家样本.2)权重系数的学习.先运行对抗生成式模仿学习算法, 再利用奖励函数预测的样本排序和真实排序计算排序误差作为损失函数, 优化专家样本的权重系数.通过权重系数对专家数据进行重分布, 使其数据分布进一步接近最优专家策略, 进而提高模仿学习算法性能.

图1 GLANCE流程图Fig.1 Flow chart of GLANCE

2.1 训练特征提取器

模仿学习之所以能够取得出色的效果是因为其在很大程度上依赖充足的最优专家样本进行的策略学习.但在现实任务场景中, 为了提高采样效率, 常采用多个智能体策略同时进行专家样本采集, 难以保证所有专家策略性能一致.为此, 本文提出采用混合专家样本的方式, 由性能最优的策略产生的样本成为最优专家样本ξ * , 其余为次优专家样本ξ '.为了尽可能减少因直接对次优专家样本进行模仿而造成的模仿学习策略性能损失, 引入特征提取器, 使次优专家样本状态表征尽可能接近最优专家样本.

本文对比次优专家样本和最优专家样本的行为特征, 使用噪声信号模拟两者之间的差距, 这种方法被称为噪声注入[17].噪声注入只适用于次优专家样本与最优专家样本之间差异较小的情况, 噪声强度的选择也需要根据具体情况进行调整, 过强或过弱的噪声都可能影响模型效果.次优专家样本可认为是最优专家样本经由正态分布噪声$\epsilon$扰动后得到, 即

ξ '=ξ * +$\epsilon$.

假定最优专家样本状态动作对的占有率度量为ρ * (s, a), 添加正态分布噪声后的占有率度量为ρ '(s, a), 则特征提取器E(· )的优化目标为

arg minEKL(ρ * (s, a)‖ ρ '(s, a)),

即通过最小化两者的KL散度达到使次优专家样本状态表征接近最优专家样本状态表征的目的.GLANCE使用对抗生成式训练框架训练特征提取器E[· ], 引入特征判别器D(· ), 通过判断提取后的特征来源评估当前特征提取器的训练效果.

借鉴GAN[21]的思想, 特征判别器和特征提取器的损失函数分别为

LDs, a; θD=minθD⁡minθDEs, a∼ρ* Ez∼pzs, a-log⁡logDz

+Es, a∼ρ'Ez∼pzs, a-log⁡log1-Dz,

LEs, a; θE=maxθE⁡maxθEEs, a∼ρ* Ez∼pzs, a-log⁡logDz

+Es, a∼ρ'Ez∼pzs, a[-log⁡log1-Dz],

其中, z表示经过特征提取器后的特征, p(z|x)表示特征提取后生成的样本满足的条件概率分布, θ D表示特征判别器参数, θ E表示特征提取器参数.

GAIL证明优化上述极大极小值损失函数等价于优化最优专家策略和噪声专家策略占有率度量之间的KL散度, 从而使两个分布之间距离减小, 相似度提高.

随着特征提取器的引入, 最优专家样本和次优专家样本的特征分布距离减小, 可能会在训练中丢失最优专家样本的特征信息, 进而导致其退化成为次优专家样本, 造成模仿学习性能的损失.因此本文提出将特征提取前后最优专家样本的互信息[22]作为正则化项进行约束, 避免信息损失.

互信息定义为

$\begin{aligned}I(X, Z)= & \int p(x, z) \log \left(\frac{p(x, z)}{p(x) p(z)}\right) \mathrm{d} x \mathrm{~d} z= \\& \int p(x) p(z \mid x) \log \left(\frac{p(z \mid x)}{p(z)}\right) \mathrm{d} x \mathrm{~d} z, \end{aligned}$

其中, X=p(x)表示特征提取前专家样本的数据分布, Z=p(z)表示特征提取后专家样本的数据分布.难以直接通过采样计算得到

p(z)=∫ p(z|x)p(x)dx,

本文引入分布r(z), 对互信息的上界进行估计.由于

KL[p(x)‖ p(z)]≥ 0,

进而导出

∫ p(z)log p(z)dz≥ ∫ p(z)log r(z)dz,

得到I(X, Z)的上界:

$\begin{aligned} I(X, Z) \leqslant & \int p(x) p(z \mid x) \log \left(\frac{p(z \mid x)}{r(z)}\right) \mathrm{d} x \mathrm{~d} z= \\ & E_{x \sim p(x)} K L[p(z \mid x) \| r(z)], \end{aligned}$

其中, 选择分布r(z)为均值为0、方差为1的正态分布, 将互信息的上界作为特征提取器优化目标的正则化项, 从而达到减少最优专家样本信息损失的目的.完整的优化目标为:

LE(s, a; θ E)= maxθE Es, a~ρ* [Ez~p(z|s, a)[-log D(z)]]+

Es, a~ρ '[Ez~p(z|s, a)[-log(1-D(z))]]+

α Es, a~ρ* [KL[p(z|s, a)‖ r(s, a)]],

其中α 表示正则化项系数.

特征提取器的训练过程如图2所示.

图2 特征提取器训练过程Fig.2 Training process of feature extractor

2.2 训练权重系数

混合专家样本数据集的样本质量参差不齐, 如果不加以区分而直接进行无差别模仿, 会造成模仿学习策略的性能损失.因此, 本文引入权重系数β ∈ (0, 1), 用于标定专家样本的品质.权重系数的值越接近于1, 表示品质越高, 在模仿学习算法损失函数的计算中, 该样本权重占比就越大, 对该样本的模仿就越精确.

当前的混合专家策略表示为π d, 当前策略在和环境交互过程中的占有率度量为

ρπd(s, a)=π d(a|s) ∑t=0∞γ tP(st=s|π d).

通过对π d的状态动作对进行重分布后便可得到新策略π new, 其占有率度量可表示为

ρπnew(s, a)=β (s, a) ρπd(s, a).

经过权重系数重分布后的模仿学习损失函数可写作 $E_{s',a'~β(s,a)ρ^{d}(s,a)}L_{模仿}$, 其中L模仿可以是行为克隆或逆强化学习等任何传统模仿学习算法的损失函数.本文的目标就是通过权重系数, 对不同的专家样本进行差异化学习, 最大化模仿学习算法性能, 即达到最大化累计期望回报的目的.最优权重系数分布为

β * (s, a)=arg maxβ ηπnew,

其中,

$ \eta_{\pi_{\text {new }}}=E_{\left(s_{t}, a_{t}\right) \sim \rho_{\pi_{\text {new }}}}\left[\sum_{t=0}^{\infty} \gamma^{t} R\left(s_{t}, a_{t}\right)\right], $

表示重分布后策略π new的累积期望回报, R表示环境的奖励函数, γ 表示衰减系数.

权重学习的目的是最大化模仿学习算法的性能, 故可以通过对模仿学习算法的性能进行评估, 反映当前权重系数学习的效果.为此, 引入评估数据集DE, 对模仿学习算法进行评估, 引入权重损失函数反映评估效果, 并进一步优化权重系数.

在评估指标的选择上, 本文通过排序任务反映当前模仿学习算法的学习效果, 即首先预测专家样本的排序, 如果预测排序和真实排序越相符, 表示当前模仿学习算法效果越优.

评估数据集由少量已知相对排序的专家样本组成, 即

DE={η | ηξ1≥ ηξ2≥ …≥ ηξk}.

权重损失选择Margin Ranking Loss[23].

2.3 算法介绍

1)特征提取器学习.首先需要训练特征提取器.从混合专家样本数据集T上挑选最优专家样本构成数据集T* .向其中的样本添加正态分布噪声$\epsilon$, 获得噪声专家样本数据集T'.根据2.1节的方法, 通过噪声对比估计, 训练得到特征提取器E.为了使模仿学习策略和权重系数能得到稳定有效的训练, 本文选择一种交替式的优化框架, 分别对模仿学习策略参数θ 和权重系数β 进行交替优化.

2)模仿学习.在模仿学习训练阶段, 本文选用对抗式逆强化学习(Adversarial IRL, AIRL)[9]作为基础模型, AIRL延续GAIL[8]的学习范式, 在GAIL的基础上进行奖励构造, 将奖励拆解为

R(s, a, s')=g(s, a)+γ h(s')-h(s),

其中, g(· )由与状态-动作有关的奖励函数组成, h(· )由只与状态有关的奖励函数组成.AIRL证明, 这种奖励构造可以使算法针对环境的MDP改变, 具有更强的鲁棒性, 不同于GAIL, AIRL训练的产出结果不仅包括策略函数π , 还包括奖励函数R, 可投放到相似的测试环境中直接使用, 从而减小因频繁更换环境而重新训练的计算代价.

AIRL由策略网络π θ 和奖励函数网络Rθ 构成, 通过对抗生成式的训练方式, 使生成器生成样本尽可能接近专家样本的占有率度量.奖励函数网络R的损失函数为:

L模仿R(s, a; θ R, β )= Es', a'~E(πnew(s, a))-log R(s', a')]+Es', a'~E(π (s, a))[-log(1-R(s', a'))].

策略网络π 的损失函数为:

L模仿π(s, a; θ π )=Es', a'~E(π (s, a))[log R(s', a')-log(1-R(s', a'))].

其中E表示噪声对比估计阶段训练收敛的特征提取器.

3)权重学习.在权重学习阶段, 本文采用相对排序预测评估模仿学习阶段学习到的策略性能.收集少量已知相对排序的专家样本ζ 作为评估数据集, 经由AIRL训练后的奖励函数R预测的累计期望回报为:

η ' ζi= ∑t=0∞γ tR(s't, a't).

已知真实累计期望回报为η ζ , 从评估数据集上抽取若干条样本数据对, 排序损失定义为

L权重= ∑i∑j> iRank[η ' ζi, η ' ζj; I[ ηζi> ηζj]],

其中,

$\operatorname{Rank}\left[\eta_{\zeta_{i}}^{\prime}, \eta_{\zeta_{j}}^{\prime} ; I\left[\eta_{\zeta_{i}}> \eta_{\zeta_{j}}\right]\right]=\left\{\begin{array}{ll} \max \left(0, -I\left[\eta_{\zeta_{i}}> \eta_{\zeta_{j}}\right]\left(\eta_{\zeta_{i}}^{\prime}-\eta_{\zeta_{\zeta_{j}}}^{\prime}\right)\right), & \left|\eta_{\zeta_{i}}^{\prime}> \eta_{\zeta_{j}}^{\prime}\right|> \tau \\ \max \left(0, \frac{1}{4 \epsilon} I\left[\eta_{\zeta_{i}}> \eta_{\zeta_{j}}\right]\left(\left(\eta_{\zeta_{i}}^{\prime}-\eta_{\zeta_{j}}^{\prime}\right)-\tau\right)^{2}\right), & \left|\eta_{\zeta_{i}}^{\prime}> \eta_{\zeta_{j}}^{\prime}\right| \leqslant \tau \end{array}\right. $

I[· ]表示指示函数, 当 ηζi> ηζj时, I[ ηζi, ηζj]=1, 否则I[ ηζi, ηζj]=-1, τ =10-5, 表示拉普拉斯平滑系数.

4)模仿学习阶段和权重学习阶段交替执行, 迭代优化.权重学习通过评估模仿学习当前的性能, 计算排序损失并优化权重系数.模仿学习基于权重学习重分布后的样本分布进行学习, 完成对最优专家样本的模仿, 达到最大化累计期望回报的目的.

3 实验及结果分析
3.1 实验环境

本文在OpenAI gym[24]的MuJoCo(Mutil-Joint Dynamics with Contact)[25]仿真环境中进行对照实验.MuJoCo是一个模拟机器人、生物力学、图形和动画等领域的物理引擎, 常用于基于模型的计算、逆动力学的数据分析及强化学习算法的应用测试.本文选取其中6种机器人连续控制任务作为本次的实验环境, 分别为:Ant(训练四足机器人学会行走); Pusher(训练机械臂将物体推向指定位置); Half-Cheetah(训练二足机器人学会行走); Swimmer(训练粘性流体中的三连杆机器人, 控制两个关节, 使其尽可能快地往前游泳); Reacher(训练两连杆机器人不断去接近一个目标); Pendulum(训练机器人保持倒立摆不要掉落).实验环境示意图如图3所示.

图3 MuJoCo 训练仿真环境示意图Fig.3 Sketch map of MuJoCo training simulation environment

6种机器人控制任务均为强化学习和模仿学习中常用测试基准环境.本文分别在每个测试环境中收集最优专家样本及次优专家样本共同构建数据集, 验证算法在混合专家样本数据集设定下的有效性.

本文选用的实验评估指标为累计期望回报.将不同算法在训练环境中训练收敛的智能体置于测试环境中, 使其与测试环境交互, 并在此期间不断收集测试环境给予的真实奖励反馈, 对累计的真实奖励进行统计, 获得累计期望回报.累计期望回报越高, 表示当前策略学习程度越高, 性能越优.

对于不同的连续动作控制任务, 伴随着状态空间和动作空间维度的增加, 控制难度也逐渐上升.各MuJoCo控制任务的状态空间和动作空间的维度、算法参数设置如表1所示.

表1 GLANCE在不同MuJoCo测试任务上的参数设置 Table 1 Parameter settings of GLANCE in different MuJoCo test tasks
3.2 数据采集

模仿学习需要以事先收集的人类专家执行当前任务的专家样本为示例进行学习.本文采用已训练收敛的强化学习智能体作为专家进行样本收集, 选择近端策略优化算法(Proximal Policy Optimiza-tion, PPO)[26]作为专家智能体的训练算法.为了能够收集到混合专家样本数据, 在MuJoCo实验环境中使用物理引擎定义的真实奖励函数训练PPO至收敛, 保存训练过程中的4个中间策略模型参数, 作为次优专家策略, 保存最终收敛的策略模型作为最优专家策略.让这5个策略模型分别和环境交互, 收集40 000条轨迹数据, 混合后构成最终的混合专家样本数据集.另外, 本文选择其中5%的数据, 标注相对排序信息, 作为评估数据集, 用于评估权重损失.

3.3 基线算法

1)标准模仿学习算法.GAIL[8]和AIRL[9].

2)基于排序的方法.

(1)T-REX[16].标注相对排序的数据训练二分类器, 训练好的分类器保存专家样本之间相对排序的判别知识, 可以在测试时为更优的专家样本给予更高的打分.

(2)D-REX[17].进一步改进T-REX, 基于小批量最优专家样本, 通过行为克隆训练最优策略, 向最优策略中不断注入噪声, 产生具有相对排序的次优专家样本, 节约人工标注的成本.

3)基于权重的方法.

(1)2IWIL[11].利用少量标注权重系数的专家样本训练预测器, 并通过该预测器预测大量无监督数据的权重系数, 根据权重系数重分布后的专家样本完成模仿学习的训练.

(2)IC-GAIL[11].在2IWIL的基础上, 使用端到端的方式训练, 通过占有率度量匹配, 使策略分布接近最优策略分布.

(3)CAIL[10].采用自适应的权重系数优化方式, 未针对次优专家样本和最优专家样本的特征分布差异做出特定优化.

3.4 对比实验

本节将GLANCE的实验效果和近年同类算法进行横向对比.GAIL和AIRL直接从混合专家样本中进行学习.T-REX和D-REX需要预先排好相对顺序的专家样本对, 因此本文提供和GLANCE中评估数据集相同数量的专家样本对.D-REX需要额外提供噪声扰动的专家样本, 因此本文按照文献[17]提供相应的噪声样本.另外, 本文选用AIRL作为2IWIL、IC-GAIL和CAIL的基础算法.

本文使用PPO[26]作为专家策略进行数据采集, 也可选用TRPO(Trust Region Policy Optimiza-tion)[27]、SAC(Soft Actor-Critic)[28]或其它策略梯度优化算法.特征提取器、特征判别器、策略网络、奖励函数网络等架构均为两层全连接网络, 激活函数选择ReLU[29].

训练与评估都在NVIDIA A100 GPU上完成, 算法通过PyTorch[30]框架进行部署.

为了保证实验对照的公平性, 所有实验均在相同数据集上设置5个随机种子, 通过运行后得到的平均值进行性能对比.在每个测试环境上执行2 000 000步训练, 并记录策略生成轨迹的奖励回报随训练步数的变化情况, 具体如图4所示.由图可以直观看到, 待算法收敛后, GLANCE的训练结果均最优.

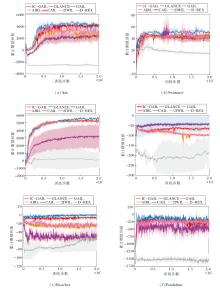图4 各算法在 MuJoCo 仿真环境中的累计期望回报曲线Fig.4 Cumulative expected return curves of different algorithms in MuJoCo simulation environment

各算法收敛后的累计期望回报平均值如表2所示, 表中黑体数字表示最优值.由表可见, D-REX、T-REX由于无法获得原论文实验设定下的大量人工标注相对排序的专家样本, 性能大幅衰减, 整体处于落后水平.GAIL和AIRL由于算法本身没有针对混合专家样本做出特定的优化, 性能表现也相对较差.CAIL在所有的测试环境中的性能表现均不及GLANCE, 这验证特征提取器模块及噪声对比估计学习范式的有效性.

表2 各算法在MuJoCo仿真环境中的累计期望回报 Table 2 Cumulative expected return of different algorithms in MuJoCo simulation environment

综上所述, 在混合专家样本的实验设定下, 在相同规模的数据集及相同网络参数设定的训练中, GLANCE取得最优的性能表现.

3.5 消融实验

本节分别针对特征提取器、权重系数优化及评估数据集规模进行消融实验, 验证上述模块在GLANCE中的有效性.特征提取器的作用在于对次优专家样本的状态表征进行重分布, 使其可以更加接近最优专家样本的状态分布, 提升数据质量, 进而提升整个算法的性能表现.

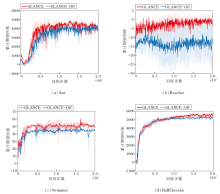
为了验证特征提取器的有效性, 本文在Ant、Reacher、Swimmer、HalfCheetah环境中分别对GLANCE和去除特征提取器的GLANCE(记为GLANCE-Off)进行对比实验, 累计期望回报随训练步数变化的曲线如图5所示.由图分析可知, 在算法训练达到收敛之后, GLANCE的性能明显优于GLANCE-Off.

图5 有无特征提取器的累计期望回报曲线Fig.5 Cumulative expected return curves with and without feature extractor

GLANCE和GLANCE-Off收敛后的累计期望回报的平均值如表3所示.由表可知, 去除特征提取器后, 虽然算法仍能达到收敛, 但性能受到不同程度的损失, 因此特征提取器模块在 GLANCE中的作用是不可或缺的.

表3 有无特征提取器的累计期望回报 Table 3 Cumulative expected return with and without feature extractor

权重系数的作用在于进一步区分特征提取之后的样本, 使品质更高的样本对应的权重系数更高, 在模仿学习的损失计算中占有更高的比重.让模仿学习在优化过程中着重于对最优专家样本的优化, 并尽可能多而有效地利用次优专家样本提升算法性能.

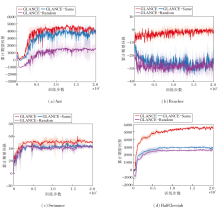
为了验证可学习权重系数的有效性, 本文在Ant、Reacher、Swimmer、HalfCheetah环境中分别使用GLANCE、初始化为1的相同权重系数(记为GLANCE-Same)、满足标准正态分布的随机权重系数(记为GLANCE-Random)进行实验对比, 累计期望回报随训练步数变化的曲线如图6所示.由图分析可知, 在算法训练达到收敛之后, GLANCE性能表现最优, GLANCE-Same次之, GLANCE-Random表现最差.

图6 不同权重系数的累计期望回报曲线Fig.6 Cumulative expected return curves with different weight coefficients

算法收敛后的平均累计期望回报如表4所示.由表分析可知, 相比于固定相同的权重系数以及随机分布的权重系数, 可优化的权重系数可显著提高GLANCE性能.

表4 不同权重系数的累计期望回报 Table 4 Cumulative expected return with different weight coefficients

GLANCE的权重训练过程依赖评估数据集.评估数据集包含已知相对排序的专家样本, 用于评估当前模仿学习的训练效果.在现实任务场景中, 专家样本相对排序往往依赖人工标注, 出于对人工成本的考虑, 难以获取较大规模的评估数据集, 因此本文设计消融实验, 探究评估数据集规模对算法性能的影响.除了GLANCE以外, 依赖已标注的相对排序的专家样本进行训练的算法还包括2IWIL、IC-GAIL和T-REX.2IWIL和IC-GAIL需要专家样本的真实奖励作为先验知识, 将每个专家样本的真实奖励经过归一化后作为权重系数对数据集样本进行重分布, 并进行对抗生成式训练.T-REX依赖相对排序的先验知识作为监督信号, 使用Luce-Shephard Choice Rule[31]作为损失函数训练奖励函数, 再将训练好的奖励函数投放到前向强化学习中进行后续的学习.

为此本文在Reacher环境中, 分别使用混合专家样本中1%, 2%, 10%, 20%, 50%, 100%的数据, 对其相对排序进行标注, 并将对比算法在不同规模的标注数据集上进行训练, 结果如表5所示.由表分析可知, T-REX对评估数据集的规模具有较高要求, 性能随评估数据集的规模增大而显著升高, 在现实任务场景中难以获得大规模标注数据, 这也是T-REX的缺陷之一.2IWIL、IC-GAIL和GLANCE在标注数据规模达到全部数据规模的10%时便取得较好的性能表现, 因此性能表现不受评估数据集规模这一客观条件的约束, 更节省标注数据的人力成本.GLANCE的性能远优于2IWIL和IC-GAIL, 表现最佳.

表5 Reacher环境中各算法在不同规模评估数据集上的累计期望回报 Table 5 Cumulative expected return of different algorithms in Reacher environment on evaluation datasets of different scales
4 结束语

本文提出基于噪声对比估计的权重自适应对抗生成式模仿学习算法(GLANCE).以互信息作为约束, 对专家样本进行噪声对比估计以训练特征提取器.交替进行模仿学习和权重系数优化, 通过改良数据分布提高模仿学习算法的性能上限.在多个环境上的实验证实GLANCE在混合专家样本设定下的性能较优, 并且仅需要少量人工标注数据(5%), 便可取得优异的性能表现.目前GLANCE仍依赖人工标注排序作为先验知识, 因此如何从无监督的混合专家样本中进行数据挖掘从而提升模仿学习性能是今后的研究方向之一.

本文责任编委 杨 明

Recommended by Associate Editor YANG Ming

参考文献
[1] ARGALL B D, CHERNOVA S, VELOSO M, et al. A Survey of Robot Learning from Demonstration. Robotics and Autonomous Systems, 2009, 57(5): 469-483. [本文引用:2]
[2] SUTTON R S, BARTO A G. Reinforcement Learning: An Introduction. 2nd Edition. Cambridge, USA: MIT Press, 2018. [本文引用:2]
[3] BAIN M, SAMMUT C. A Framework for Behavioural Cloning. Ma-chine Intelligence, 1995, 15: 103-129. [本文引用:1]
[4] ROSS S, BAGNELL J A. Efficient Reductions for Imitation Learning // Proc of the 13th International Conference on Artificial Intelligence and Statistics. San Diego, USA: JMLR, 2010: 661-668. [本文引用:1]
[5] ROSS S, GORDON G, BAGNELL D. A Reduction of Imitation Lear-ning and Structured Prediction to No-regret Online Learning // Proc of the 14th International Conference on Artificial Intelligence and Statistics. San Diego, USA: JMLR, 2011: 627-635. [本文引用:1]
[6] SHALEV-SHWARTZ S. Online Learning and Online Convex Optimization. Foundations and Trends® in Machine Learning, 2011, 4(2): 107-194. [本文引用:1]
[7] ABBEEL P, NG A Y. Apprenticeship Learning via Inverse Reinforcement Learning // Proc of the 21st International Conference on Machine Learning. New York, USA: ACM, 2004. DOI: DOI:10.1145/1015330.1015430. [本文引用:1]
[8] HO J, ERMON S. Generative Adversarial Imitation Learning[C/OL]. [2022-10-15]. https://arxiv.org/pdf/1606.03476.pdf. [本文引用:6]
[9] FU J, LUO K, LEVINE S. Learning Robust Rewards with Adversa-rial Inverse Reinforcement Learning[C/OL]. [2022-10-15]. https://arxiv.org/pdf/1710.11248.pdf. [本文引用:3]
[10] ZHANG S Y, CAO Z J, SADIGH D, et al. Confidence-Aware Imitation Learning from Demonstrations with Varying Optimality[C/OL]. [2022-10-15]. https://arxiv.org/pdf/2110.14754.pdf. [本文引用:4]
[11] WU Y H, CHAROENPHAKDEE N, BAO H, et al. Imitation Lear-ning from Imperfect Demonstration // Proc of the 36th International Conference on Machine Learning. San Diego, USA: JMLR, 2019: 6818-6827. [本文引用:6]
[12] PENG X B, ABBEEL P, LEVINE S, et al. DeepMimic: Example-Guided Deep Reinforcement Learning of Physics-Based Character Skills. ACM Transactions on Graphics, 2018, 37(4). DOI: DOI:10.1145/3197517.3201311. [本文引用:1]
[13] RAFAILOV R, YU T H, RAJESWARAN A, et al. Visual Adver-sarial Imitation Learning Using Variational Models[C/OL]. [2022-10-15]. https://arxiv.org/pdf/2107.08829.pdf. [本文引用:1]
[14] FINN C, YU T H, ZHANG T H, et al. One-Shot Visual Imitation Learning via Meta-Learning // Proc of the 1st Annual Conference on Robot Learning. San Diego, USA: JMLR, 2017: 357-368. [本文引用:1]
[15] YU T H, FINN C, XIE A N, et al. One-Shot Imitation from Observing Humans via Domain-Adaptive Meta-Learning[C/OL]. [2022-10-15]. https://arxiv.org/pdf/1802.01557.pdf. [本文引用:1]
[16] BROWN D, GOO W, NAGARAJAN P, et al. Extrapolating Beyond Suboptimal Demonstrations via Inverse Reinforcement Lear-ning from Observations // Proc of the 36th International Conference on Machine Learning. San Diego, USA: JMLR, 2019: 783-792. [本文引用:2]
[17] BROWN D S, GOO W, NIEKUM S. Better-Than-Demonstrator Imi-tation Learning via Automatically-Ranked Demonstrations[C/OL]. [2022-10-15]. http://proceedings.mlr.press/v100/brown20a/brown20a.pdf. [本文引用:4]
[18] CHEN L T, PALEJA R R, GOMBOLAY M. Learning from Suboptimal Demonstration via Self-Supervised Reward Regression // Proc of the 4th Conference on Robot Learning. San Diego, USA: JMLR, 2020: 1262-1277. [本文引用:1]
[19] XU H R, ZHAN X Y, YIN H L, et al. Discriminator-Weighted Offline Imitation Learning from Suboptimal Demonstrations // Proc of the 39th International Conference on Machine Learning. San Diego, USA: JMLR, 2022: 24725-24742. [本文引用:1]
[20] BELIAEV M, SHIH A, ERMON S, et al. Imitation Learning by Estimating Expertise of Demonstrators // Proc of the 39th International Conference on Machine Learning. San Diego, USA: JMLR, 2022: 1732-1748. [本文引用:1]
[21] GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Gene-rative Adversarial Networks. Communications of the ACM, 2020, 63(11): 139-144. [本文引用:2]
[22] KRASKOV A, STÖGBAUER H, GRASSBERGER P. Estimating Mutual Information. Physical Review E, 2004, 69. DOI: DOI:10.1103/PhysRevE.69.066138. [本文引用:1]
[23] HERBRICH R, GRAEPEL T, OBERMAYER K. Large Margin Rank Boundaries for Ordinal Regression // SMOLA A J, BARTLETT P L, SCHÖLKOPF B, et al. , eds. Advances in Large Margin Classifiers. Cambridge, USA: MIT Press, 2000: 115-132. [本文引用:1]
[24] BROCKMAN G, CHEUNG V, PETTERSSON L, et al. OpenAI Gym[C/OL]. [2022-10-15]. https://arxiv.org/pdf/1606.01540.pdf. [本文引用:1]
[25] TODOROV E, EREZ T, TASSA Y. MuJoCo: A Physics Engine for Model-Based Control // Proc of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington, USA: IEEE, 2012: 5026-5033. [本文引用:1]
[26] SCHULMAN J, WOLSKI F, DHARIWAL P, et al. Proximal Policy Optimization Algorithms[C/OL]. [2022-10-15]. https://arxiv.org/pdf/1707.06347.pdf. [本文引用:2]
[27] SCHULMAN J, LEVINE S, MORITZ P, et al. Trust Region Policy Optimization // Proc of the 32nd International Conference on Machine Learning. San Diego, USA: JMLR, 2015: 1889-1897. [本文引用:1]
[28] HAARNOJA T, ZHOU A, ABBEEL P, et al. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor // Proc of the 35th International Conference on Machine Learning. San Diego, USA: JMLR, 2018: 1861-1870. [本文引用:1]
[29] AGARAP A F M. Deep Learning Using Rectified Linear Units (ReLU)[C/OL]. [2022-10-15]. https://arxiv.org/pdf/1803.08375.pdf. [本文引用:1]
[30] PASZKE A, GROSS S, MASSA F, et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library[C/OL]. [2022-10-15]. https://papers.nips.cc/paper/2019/file/bdbca288fee7f92f2bfa9f7012727740-Paper.pdf. [本文引用:1]
[31] LUCE R D. Individual Choice Behavior: A Theoretical Analysis. New York, USA: Dover Publication, 2005. [本文引用:1]